四元数系列 - 4 四元数与三维旋转

讨论四元数与三维空间中旋转的关系.

本文主要整理自 Krasjet 的 "四元数与三维旋转" 第三章.

1 四元数与三维空间中的旋转

回忆前一节中讨论的内容:

要计算一个向量 绕一个单位向量定义的旋转轴 旋转 角度, 可以将向量 沿旋转轴的正交方向与平行方向进行分解 , 然后分别对这两个分量进行旋转得到 和 , 再将它们相加即为向量 旋转后的结果 .

我们可以将这些向量定义为纯四元数:

$$\begin{align*} v&=[0,\boldsymbol{v}]&v'&=[0,\boldsymbol{v}']\\ v_{\perp}&=[0,\boldsymbol{v}_{\perp}]&v_{\perp}'&=[0,\boldsymbol{v}_{\perp}']\\ v_{\Vert}&=[0,\boldsymbol{v}_{\Vert}]&v_{\Vert}'&=[0,\boldsymbol{v}_{\Vert}']\\ u&=[0,\boldsymbol{u}]&& \end{align*}$$

那么

$$v=v_{\perp}+v_{\Vert} \qquad v'=v_{\perp}'+v_{\Vert}'$$

下面分别讨论垂直分量 和平行分量 的旋转.

1.1 垂直分量的旋转

根据之前的推导, 若向量 正交于旋转轴 , 则

$$\boldsymbol{v}_{\perp}'=\cos(\theta)\boldsymbol{v}_{\perp}+\sin(\theta)(\boldsymbol{u}\times\boldsymbol{v}_{\perp})\tag{1}$$

要将该式转换为四元数的形式, 还须探讨 .

基于纯四元数的性质, 我们知道, 对于两个纯四元数 , , 有

$$u\star v_{\perp}=[-\boldsymbol{u}\cdot\boldsymbol{v}_{\perp}, \boldsymbol{u}\times\boldsymbol{v}_{\perp}]$$

由于此处 , 因此 依然是一个纯四元数.

$$u\star v_{\perp}=[0, \boldsymbol{u}\times\boldsymbol{v}_{\perp}]$$

现在可以将式 (1) 代换为四元数的形式, 并根据乘法分配律作变换

$$\begin{align*} v_{\perp}' &=\cos(\theta)v_{\perp}+\sin(\theta)(u\star v_{\perp})\\ &=\left(\cos(\theta)+\sin(\theta)u\right)\star v_{\perp} \end{align*}$$

令 作为一个四元数, 绕 的旋转便转换为四元数乘积的形式.

这样的 也容易构造:

$$\begin{align*} q&=\cos(\theta)+\sin(\theta)u\\ &=[\cos(\theta),\boldsymbol{0}]+[0,\sin(\theta)\boldsymbol{u}]\\ &=[\cos(\theta),\sin(\theta)\boldsymbol{u}] \end{align*}$$

因此得到以下结论:

当 正交于单位向量定义的旋转轴 时, 旋转 角度后的 可以通过四元数乘法获得. 令 , , 则:

$$v_{\perp}'=q\star v_{\perp}$$

另外由于 , 因此

$$\Vert q\Vert=\sqrt{\cos^2(\theta)+\sin^2(\theta)\Vert\boldsymbol{u}\Vert^2}=1$$

这里构造出来的 为单位四元数. 类比复数与旋转的关系, 这里的 代表的变换对于原向量只是一个纯旋转, 而不产生缩放.

1.2 平行分量的旋转

根据之前的讨论, 若一个向量 平行于旋转轴 , 则旋转后保持不变. 因此 旋转 角度后的 用四元数表示为

$$v_{\Vert}'=v_{\Vert}$$

1.3 三维空间向量的旋转

根据上述结论, 我们可以得到一般情况下 的结果

$$v'=v_{\Vert}+v_{\perp}=v_{\Vert}+q\star v_{\perp}\tag{2}$$

其中 .

在进一步讨论之前, 先引入几个引理.

引理 1: 若 , 且 为单位向量, 则 .

这个引理很容易通过 Graßmann 积证明. 其几何意义为, 绕旋转轴 连续旋转 角度两次, 相当于直接绕旋转轴 旋转 角度.

引理 2: 设 为纯四元数, , 其中 为单位向量, . 若 平行于 , 则 .

引理 3: 设 为纯四元数, , 其中 为单位向量, . 若 正交于 , 则 .

引理 2 和 3 也都容易通过 Graßmann 积证明, 证明过程中注意条件 , 即可.

令 , 即 . 可验证, 也是一个单位四元数, 即 .

基于以上三个引理, 我们对式 (2) 进行变形:

$$\begin{align*} v'&=v_{\Vert}+q\star v_{\perp}\\ &=1\cdot v_{\Vert}+q\star v_{\perp}\\ &=p\star p^{-1}\star v_{\Vert}+p\star p\star v_{\perp}\\ &=p\star p^{\ast}\star v_{\Vert}+p\star p\star v_{\perp}\\ &=p\star v_{\Vert}\star p^{\ast}+p\star v_{\perp}\star p^{\ast}\\ &=p\star(v_{\Vert}+v_{\perp})\star p^{\ast}\\ &=p\star v\star p^{\ast} \end{align*}$$

至此, 我们成功地用四元数乘法表示了三维空间中的旋转:

任意向量 沿着以单位向量定义的旋转轴 旋转 角度后的向量 可以使用四元数乘法来获得. 令 , , 则

$$v'=q\star v\star q^{\ast}=q\star v\star q^{-1}\tag{3}$$

可以证明, 式 (3) 与之前推导的罗德里格旋转公式完全等价:

$$q\star v\star q^{\ast}=[0,\cos(\theta)\boldsymbol{v}+(1-\cos(\theta))(\boldsymbol{u}\cdot\boldsymbol{v})\boldsymbol{u}+\sin(\theta)(\boldsymbol{u}\times\boldsymbol{v})]$$

证明中需要用到叉乘公式 , 以及倍角公式 , .

对于所有形如上式中 这样的旋转四元数, 它们的实部只是一个角度的余弦值. 因此对于单位四元数 , 我们可以直接获得它所对应的旋转角度 和旋转轴 :

$$\theta=2\cdot\arccos(a)\qquad\boldsymbol{u}=\frac{\boldsymbol{b}}{\sin(\arccos(a))}$$

2 三维旋转的矩阵形式

从式 (3) 可以容易地推导出四元数旋转的矩阵形式.

根据之前介绍的四元数矩阵形式, 左乘四元数 等同于左乘矩阵:

$$L(q)=\begin{bmatrix} s&-x&-y&-z\\ x& s&-z& y\\ y& z& s&-x\\ z&-y& x& s \end{bmatrix}$$

右乘四元数 等同于左乘矩阵:

$$R(q)=\begin{bmatrix} s&-x&-y&-z\\ x& s& z&-y\\ y&-z& s& x\\ z& y&-x& s \end{bmatrix}$$

设 , , , , , 可以将 改写为矩阵形式:

$$\begin{align*} q\star v\star q^{\ast} &=L(q)R(q^{\ast})v=L(q)R(q)^Tv\\ &=\begin{bmatrix} s&-x&-y&-z\\ x& s&-z& y\\ y& z& s&-x\\ z&-y& x& s \end{bmatrix}\begin{bmatrix} s&x&y&z\\ -x&s&-z&y\\ -y&z& s&-x\\ -z&-y&x& s \end{bmatrix}v\\ &=\begin{bmatrix} 1&0&0&0\\ 0&1-2y^2-2z^2&2xy-2sz&2sy+2xz\\ 0&2xy+2sz&1-2x^2-2z^2&2yz-2sx\\ 0&2xz-2sy&2sx+2yz&1-2x^2-2y^2 \end{bmatrix}v \end{align*}$$

以上就是三维旋转的四元数矩阵形式. 矩阵的右下 部分即为三维空间中的轴角旋转矩阵.

任意向量 沿着以单位向量定义的旋转轴 旋转 角度后的向量 可以使用矩阵乘法得到. 令 , , , , 则

$$\boldsymbol{v}'=\begin{bmatrix} 1-2y^2-2z^2&2xy-2sz&2sy+2xz\\ 2xy+2sz&1-2x^2-2z^2&2yz-2sx\\ 2xz-2sy&2sx+2yz&1-2x^2-2y^2 \end{bmatrix}\boldsymbol{v}$$

3 旋转的复合

引理 4: 对任意四元数 , , 有 .

该引理很容易通过 Graßmann 积证明. 转换为矩阵形式为 , 结论也是显然的.

假设有两个表示沿着不同轴不同角度旋转的四元数 , 我们先对 进行 的旋转, 再进行 的旋转. 第一次变换的结果 与第二次变换的结果 分别表示为

$$\begin{align*} v'&=q_1\star v\star q_1^{\ast}\\ v''&=q_2\star v'\star q_2^{\ast}\\ &=q_2\star q_1\star v\star q_1^{\ast}\star q_2^{\ast}\\ &=(q_2\star q_1)\star v\star(q_2\star q_1)^{\ast} \end{align*}$$

令 , 则两个旋转可复合为一个等价的旋转 .

注意, 这里的等价旋转并不是先后沿着 和 的两个旋转轴进行两次旋转, 而是沿着一个全新的轴进行一次等价旋转, 只有最终的旋转结果相同.

四元数乘法的顺序和矩阵或函数类似, 都是从右往左叠加, 很容易推广到多个旋转的复合. 此时若再进行第三个旋转 , 则

$$\begin{align*} v'''&=q_3\star(q_2\star q_1)\star v\star(q_2\star q_1)^{\ast}\star q_3^{\ast}\\ &=(q_3\star q_2\star q_1)\star v\star(q_3\star q_2\star q_1)^{\ast} \end{align*}$$

等价复合旋转即为 .

4 双倍覆盖

四元数与三维旋转的关系不是一对一的, 同一个三维旋转可以用两个不同的四元数来表示.

对任意的单位四元数 ,

$$\begin{align*} -q&=\left[-\cos\left(\frac{1}{2}\theta\right),-\sin\left(\frac{1}{2}\theta\right)\boldsymbol{u}\right]\\ &=\left[\cos\left(\pi-\frac{1}{2}\theta\right),\sin\left(\pi-\frac{1}{2}\theta\right)(-\boldsymbol{u})\right] \end{align*}$$

表示沿着相反的旋转轴 旋转 角度, 与 表示的是同一个旋转. 从下图也可以看出两个旋转完全等价.

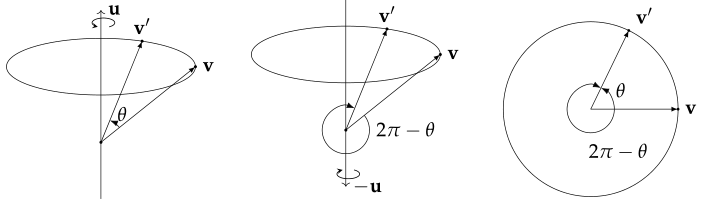
单位四元数与三维旋转之间的映射为 "2 对 1 满射同态" (2-1 Surjective Homomorphism), 或者说单位四元数双倍覆盖 (Double Cover) 了三维旋转. 所有的单位四元数都对应着一个三维旋转.

虽然 与 为不同的单位四元数, 但它们的旋转矩阵是完全相同的, 因此旋转矩阵不会出现双倍覆盖的问题.

5 指数形式

与复数的欧拉公式类似, 四元数也有一个类似的公式.

若 为单位向量, 那么对于单位四元数 , 有

$$e^{u\theta}=\cos(\theta)+u\sin(\theta)=\cos(\theta)+\boldsymbol{u}\sin(\theta)$$

因此, 可以使用指数表示为 . 该公式证明与欧拉公式证明类似, 使用级数展开即可, 证明过程见原文附录1.

利用指数表示, 可以将式 (3) 的四元数旋转公式改写为指数形式:

任意向量 沿着以单位向量定义的旋转轴 旋转 角度后的向量 可以使用四元数的指数形式表示. 令 , , 则

$$v'=e^{u\frac{\theta}{2}}\star v\star e^{-u\frac{\theta}{2}}$$

有了四元数的指数形式, 便可定义自然对数形式, 对任意单位四元数 ,

$$\log(q)=\log(e^{u\theta})=[0,\boldsymbol{u}\theta]$$

进而可定义单位四元数的幂运算

$$q^t=(e^{u\theta})^t=e^{u(t\theta)}=[\cos(t\theta),\sin(t\theta)\boldsymbol{u}]$$

可以看到, 一个单位四元数的 次幂等同于将它的旋转角度缩放至 倍, 且不会改变旋转轴.

参考文献

1. Krasjet. 四元数与三维旋转[OL]. https://github.com/Krasjet/quaternion
2. Andrew J. Hanson. Visualizing Quaternions[M]. Elsevier. 2004.