四元数系列 - 3 四元数

四元数的基本定义与性质.

本文主要整理自 Krasjet 的 "四元数与三维旋转" 第三章.

四元数 (Quaternion) 的定义与复数非常类似, 唯一的区别是: 四元数有三个虚部, 而复数只有一个虚部.

1 定义

定义形如 (其中 且 ) 的数叫做四元数, 全体四元数的集合记作 (H 代表四元数的发现者 William Rowan Hamilton).

与复数类似, 四元数为关于基 (Basis) 的线性组合, 因此可以用向量表示为:

$$q=\begin{bmatrix}a\\b\\c\\d\end{bmatrix}$$

我们经常将四元数的实部与虚部分开, 并用一个三维向量表示虚部,

$$q=[s,\boldsymbol{v}]\quad (v=\begin{bmatrix}x\\y\\z\end{bmatrix}, \enspace s,x,y,z\in\mathbb{R})$$

其中 称为四元数 的标量部分 (scalar part), 称为四元数 的向量部分 (vector part).

2 性质

2.1 四元数模长 (范数)

对于四元数 , 其模长 (范数 (Norm)) 定义为:

$$\Vert q\Vert=\sqrt{s^2+x^2+y^2+z^2}$$

对于标量向量有序对形式的表示, 的模长为:

$$\Vert q\Vert=\sqrt{s^2+\Vert\boldsymbol{v}\Vert^2}=\sqrt{s^2+\boldsymbol{v}\cdot\boldsymbol{v}}$$

其中 .

2.2 四元数加减法

对于两个四元数 , , 它们的和差即为对应分量相加减的结果:

$$\begin{align*} q_1+q_2&=(s_1+s_2)+(x_1+x_2)\mathrm{i}+(y_1+y_2)\mathrm{j}+(z_1+z_2)\mathrm{k}\\ q_1-q_2&=(s_1-s_2)+(x_1-x_2)\mathrm{i}+(y_1-y_2)\mathrm{j}+(z_1-z_2)\mathrm{k} \end{align*}$$

同理, 对于标量向量有序对形式, 如 , , 则有

$$\begin{align*} q_1+q_2&=[s_1+s_2,\boldsymbol{v}_1+\boldsymbol{v}_2]\\ q_1-q_2&=[s_1-s_2,\boldsymbol{v}_1-\boldsymbol{v}_2] \end{align*}$$

2.3 标量乘法

对于四元数 及标量 , 它们的乘积满足交换律:

$$tq=t(s+x\mathrm{i}+y\mathrm{j}+z\mathrm{k})=ts+tx\mathrm{i}+ty\mathrm{j}+tz\mathrm{k}=qt$$

2.4 四元数乘法

与复数不同, 由于四元数有三个虚部, 因此存在虚部之间相乘的特殊情况. 利用已知条件 可推导出所有乘积情况, 这里通过表格形式展示结果.

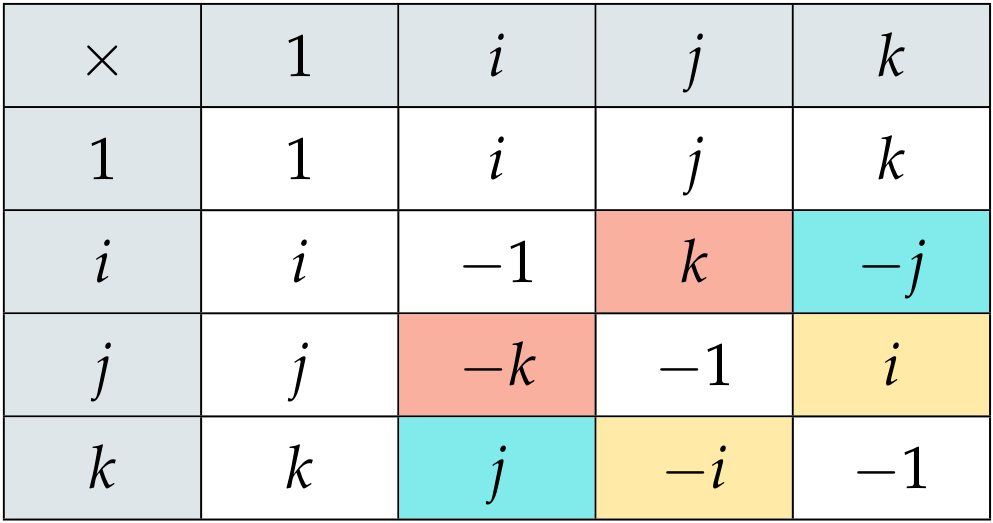
表格最左列中一个元素右乘以顶行中一个元素的结果就位于这两个元素的行列交叉处. 例如 . 从有颜色标记的格子中可以看出, 四元数乘法不成立交换律.

记四元数乘法运算符为 , 对于两个四元数 , , 它们的乘积可通过乘法分配律和结合律来计算, 并对照表格进行化简:

$$\begin{align*} q_1\star q_2=&\space(s_1+x_1\mathrm{i}+y_1\mathrm{j}+z_1\mathrm{k})(s_2+x_2\mathrm{i}+y_2\mathrm{j}+z_2\mathrm{k})\\ =&\space s_1s_2+s_1x_2\mathrm{i}+s_1y_2\mathrm{j}+s_1z_2\mathrm{k}+\\ &\space x_1s_2\mathrm{i}+x_1x_2\mathrm{i}^2+x_1y_2\mathrm{i}\mathrm{j}+x_1z_2\mathrm{i}\mathrm{k}+\\ &\space y_1s_2\mathrm{j}+y_1x_2\mathrm{j}\mathrm{i}+y_1y_2\mathrm{j}^2+y_1z_2\mathrm{j}\mathrm{k}+\\ &\space z_1s_2\mathrm{k}+z_1x_2\mathrm{k}\mathrm{i}+z_1y_2\mathrm{k}\mathrm{j}+z_1z_2\mathrm{k}^2\\ =&\space s_1s_2+s_1x_2\mathrm{i}+s_1y_2\mathrm{j}+s_1z_2\mathrm{k}+\\ &\space x_1s_2\mathrm{i}-x_1x_2+x_1y_2\mathrm{k}-x_1z_2\mathrm{j}+\\ &\space y_1s_2\mathrm{j}-y_1x_2\mathrm{k}-y_1y_2+y_1z_2\mathrm{i}+\\ &\space z_1s_2\mathrm{k}+z_1x_2\mathrm{j}-z_1y_2\mathrm{i}-z_1z_2\\ =&\space(s_1{\color{red}{s_2}}-x_1{\color{green}{x_2}}-y_1{\color{blue}{y_2}}-z_1{\color{maroon}{z_2}})+\\ &\space(x_1{\color{red}{s_2}}+s_1{\color{green}{x_2}}-z_1{\color{blue}{y_2}}+y_1{\color{maroon}{z_2}})\mathrm{i}+\\ &\space(y_1{\color{red}{s_2}}+z_1{\color{green}{x_2}}+s_1{\color{blue}{y_2}}-x_1{\color{maroon}{z_2}})\mathrm{j}+\\ &\space(z_1{\color{red}{s_2}}-y_1{\color{green}{x_2}}+x_1{\color{blue}{y_2}}+s_1{\color{maroon}{z_2}})\mathrm{k} \end{align*}$$

2.5 四元数的矩阵形式

可以发现, 与复数类似, 四元数相乘也可以写成矩阵形式:

$$q_1\star q_2= \begin{bmatrix} s_1&-x_1&-y_1&-z_1\\ x_1& s_1&-z_1& y_1\\ y_1& z_1& s_1&-x_1\\ z_1&-y_1& x_1& s_1 \end{bmatrix} \begin{bmatrix} {\color{red}{s_2}}\\ {\color{green}{x_2}}\\ {\color{blue}{y_2}}\\ {\color{maroon}{z_2}} \end{bmatrix}$$

其中, 右侧的 是向量形式表示的 , 而左侧的 则定义为 的矩阵形式, 这里用粗体大写字母记为 .

另外, 也可以将右乘的四元数表示为左乘的矩阵形式, 有少数情况会用到.

$$q_1\star q_2= \begin{bmatrix} s_2&-x_2&-y_2&-z_2\\ x_2& s_2& z_2&-y_2\\ y_2&-z_2& s_2& x_2\\ z_2& y_2&-x_2& s_2 \end{bmatrix} \begin{bmatrix} s_1\\ x_1\\ y_1\\ z_1 \end{bmatrix}$$

进一步, 若将四元数乘法中的四元数看作一种变换, 四元数乘法便可在矩阵形式下转化为矩阵乘法. 注意, 与复数乘法不同, 四元数乘法不满足交换律.

因此, 我们可以将四元数 与矩阵 建立等价关系. 进一步, 得到关于基向量 的矩阵形式:

$$\begin{align*} \mathbf{1}&=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}=I & (s=1,x=y=z=0)\\ \mathbf{i}&=\begin{bmatrix}0&-1&0&0\\1&0&0&0\\0&0&0&-1\\0&0&1&0\end{bmatrix} &(x=1,s=y=z=0)\\ \mathbf{j}&=\begin{bmatrix}0&0&-1&0\\0&0&0&1\\1&0&0&0\\0&-1&0&0\end{bmatrix} &(y=1,s=x=z=0)\\ \mathbf{k}&=\begin{bmatrix}0&0&0&-1\\0&0&-1&0\\0&1&0&0\\1&0&0&0\end{bmatrix} &(z=1,s=x=y=0) \end{align*}$$

2.6 Graßmann 积

在四元数乘法中, 换个角度观察乘积可以发现

$$\begin{align*} q_1\star q_2 =&\space(s_1s_2-({\color{green}x_1x_2+y_1y_2+z_1z_2}))+\\ &\space({\color{red}{x_1}}s_2+s_1{\color{blue}{x_2}}+{\color{maroon}y_1z_2-z_1y_2})\mathrm{i}+\\ &\space({\color{red}{y_1}}s_2+s_1{\color{blue}{y_2}}+{\color{maroon}z_1x_2-x_1z_2})\mathrm{j}+\\ &\space({\color{red}{z_1}}s_2+s_1{\color{blue}{z_2}}+{\color{maroon}x_1y_2-y_1x_2})\mathrm{k} \end{align*}$$

令 , , 那么

$$\begin{align*} \boldsymbol{v_1}\cdot\boldsymbol{v_2} =&\space{\color{green}x_1x_2+y_1y_2+z_1z_2}\\ \boldsymbol{v_1}\times\boldsymbol{v_2} =&\space\left\vert\begin{matrix}\mathrm{i}&\mathrm{j}&\mathrm{k}\\x_1&y_1&z_1\\x_2&y_2&z_2\end{matrix}\right\vert\\ =&\space({\color{maroon}y_1z_2-z_1y_2})\mathrm{i}+\\&\space({\color{maroon}z_1x_2-x_1z_2})\mathrm{j}+\\&\space({\color{maroon}x_1y_2-y_1x_2})\mathrm{k} \end{align*}$$

因此, 四元数乘法的结果也可以用向量点乘和叉乘的形式表示出来:

对任意四元数 , , 有

$$q_1\star q_2=[s_1s_2-\boldsymbol{v}_1\cdot\boldsymbol{v}_2,\space s_1\boldsymbol{v}_2+s_2\boldsymbol{v}_1+\boldsymbol{v}_1\times\boldsymbol{v}_2]$$

这个结果叫做 Graßmann 积, 它是将四元数与旋转联系起来的关键.

2.7 纯四元数

这里单独讨论四元数的一种特殊形式, 即仅有虚部的四元数:

$$v=[0,\boldsymbol{v}]$$

我们称 为纯四元数 (Pure Quaternion). 若一个三维向量为 , 我们将没有不加粗且没有上标的 记为它对应的纯四元数 . 任意三维向量都可以转换为一个纯四元数.

若有两个纯四元数 , , 那么

$$\begin{align*} v_1\star v_2&=[0-\boldsymbol{v}_1\cdot\boldsymbol{v}_2,\space 0+\boldsymbol{v}_1\times\boldsymbol{v}_2]\\ &=[-\boldsymbol{v}_1\cdot\boldsymbol{v}_2,\space \boldsymbol{v}_1\times\boldsymbol{v}_2] \end{align*}$$

纯四元数 的矩阵形式为

$$\mathbf{V}=\begin{bmatrix} 0&-x&-y&-z\\ x& 0&-z& y\\ y& z& 0&-x\\ z&-y& x& 0 \end{bmatrix}$$

显然, , 说明 为反对称矩阵 (Skew Symmetric Matrix).

2.8 四元数的共轭和逆

四元数 的共轭 (Conjugate) 定义为

$$q^\ast=s-x\mathrm{i}-y\mathrm{j}-z\mathrm{k}$$

与复数类似, 四元数共轭在矩阵形式下对应为转置运算

$$\begin{bmatrix} s&x&y&z\\ -x& s&z&-y\\ -y& -z& s&x\\ -z&y& -x& s \end{bmatrix}=\mathbf{Q}^T$$

对于标量向量有序对形式, 的共轭为 .

注意到

$$\begin{align*} q\star q^\ast&=[s,\boldsymbol{v}]\star[s,-\boldsymbol{v}]\\ &=[s^2-\boldsymbol{v}\cdot(-\boldsymbol{v}),\space s(-\boldsymbol{v})+s\boldsymbol{v}+\boldsymbol{v}\times(-\boldsymbol{v})]\\ &=[s^2+\boldsymbol{v}\cdot\boldsymbol{v},\space \boldsymbol{0}] \end{align*}$$

得到的结果是一个实数, 而它正是四元数模长的平方:

$$\begin{align*} q\star q^*&=[s^2+\boldsymbol{v}\cdot\boldsymbol{v},\space \boldsymbol{0}]\\ &=s^2+x^2+y^2+z^2\\ &=\Vert q\Vert^2 \end{align*}$$

对应的矩阵形式结果为

$$\mathbf{Q}\mathbf{Q}^T=\begin{bmatrix}\Vert q\Vert^2&&&\\&\Vert q\Vert^2&&\\&&\Vert q\Vert^2&\\&&&\Vert q\Vert^2\end{bmatrix}=\Vert q\Vert^2I$$

由于 , 容易推导出 , 因此四元数与自身共轭之间的乘法满足交换律.

四元数的逆 (Inverse) 记为 , 规定:

$$q\star q^{-1}=q^{-1}\star q=1\quad(q\neq0)$$

与矩阵类似, 右乘 的逆运算为右乘 , 左乘 的逆运算为左乘 .

四元数的求逆运算对应到矩阵形式上也是矩阵求逆运算:

$$\mathbf{Q}\mathbf{Q}^{-1}=I$$

利用共轭的性质, 可以计算四元数的逆:

$$\begin{align*} q\star q^{-1}&=1\\ q^\ast\star q\star q^{-1}&=q^\ast\\ \Vert q\Vert^2q^{-1}&=q^\ast\\ q^{-1}&=\frac{q^\ast}{\Vert q\Vert^2} \end{align*}$$

若 , 即 为单位四元数 (Unit Quaternion), 那么

$$q^{-1}=q^\ast$$

单位四元数对应到矩阵形式为

$$\mathbf{Q}^{-1}=\mathbf{Q}^T$$

这表示单位四元数的矩阵形式为正交矩阵 (Orthogonal Matrix).

参考文献

1. Krasjet. 四元数与三维旋转[OL]. https://github.com/Krasjet/quaternion
2. Andrew J. Hanson. Visualizing Quaternions[M]. Elsevier. 2004.