四元数系列 - 2 三维空间中的旋转

三维空间中旋转公式的推导.

本文主要整理自 Krasjet 的 "四元数与三维旋转" 第二章.

表示三维空间中旋转的方法有很多种, 我们这里关注轴角式 (Axis-angle) 的旋转. 我们讨论时总默认使用右手坐标系统, 并总假设旋转轴经过原点. 若旋转轴不过原点, 都可以进行 "平移到原点 - 进行旋转 - 平移回原处" 的等价操作.

假设有一个经过原点的旋转轴 , 我们需要将一个向量 沿该轴旋转 度, 变换到 :

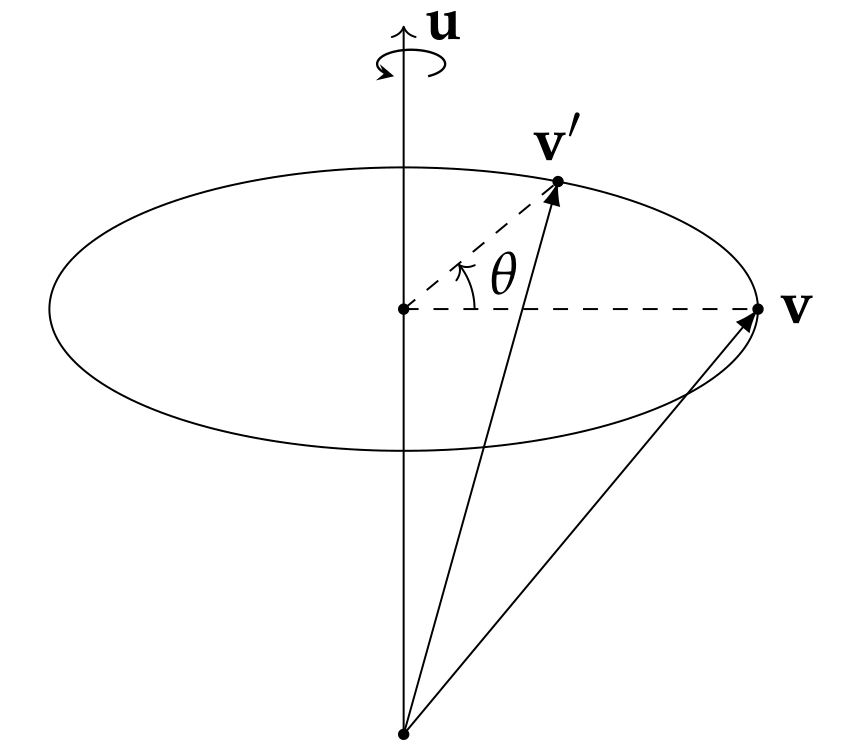
这里用 四个自由度表示一个旋转, 是冗余的. 三维空间中表示一个方向只需两个自由度, 因此通过令 来消除旋转轴模长这个多余自由度.

1 旋转的分解

已知旋转轴 (), 可以将向量 分别沿平行于 以及正交于 的方向进行分解, 得到两个分量 和 , 即

$$\boldsymbol{v}=\boldsymbol{v}_{\Vert}+\boldsymbol{v}_{\perp}\tag{1}$$

分解示意图如下:

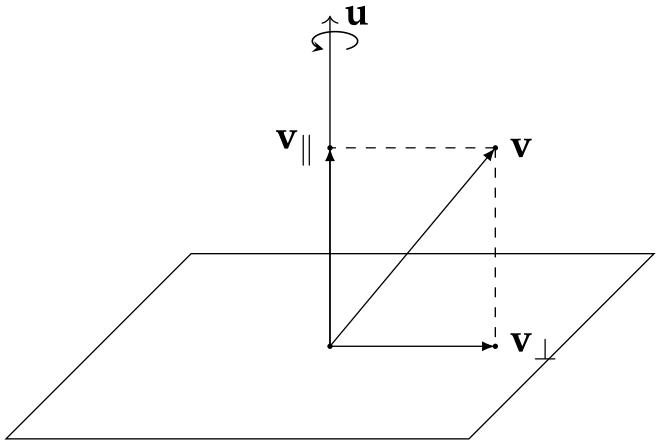
显然, 为 在 上的正交投影 (Orthogonal Projection),

$$\boldsymbol{v}_{\Vert} =\text{proj}_{\boldsymbol{u}}(\boldsymbol{v}) =\frac{\boldsymbol{u}\cdot\boldsymbol{v}}{\Vert\boldsymbol{u}\Vert^2}\boldsymbol{u} =(\boldsymbol{u}\cdot\boldsymbol{v})\boldsymbol{u} \tag{2}$$

由 (1) 式得

$$\boldsymbol{v}_{\perp} =\boldsymbol{v}-\boldsymbol{v}_{\Vert} =\boldsymbol{v}-(\boldsymbol{u}\cdot\boldsymbol{v})\boldsymbol{u} \tag{3}$$

对于旋转后的向量 , 我们可以分别绕 旋转这两个分量, 再将旋转的结果相加.

$$\boldsymbol{v}'=\boldsymbol{v}_{\Vert}'+\boldsymbol{v}_{\perp}'\tag{4}$$

2 平行分量的旋转

由于 方向与旋转轴 重合, 因此旋转后保持不变.

$$\boldsymbol{v}_{\Vert}'=\boldsymbol{v}_{\Vert}\tag{5}$$

3 垂直分量的旋转

对于 的旋转, 示意图如下, 右侧为俯视图:

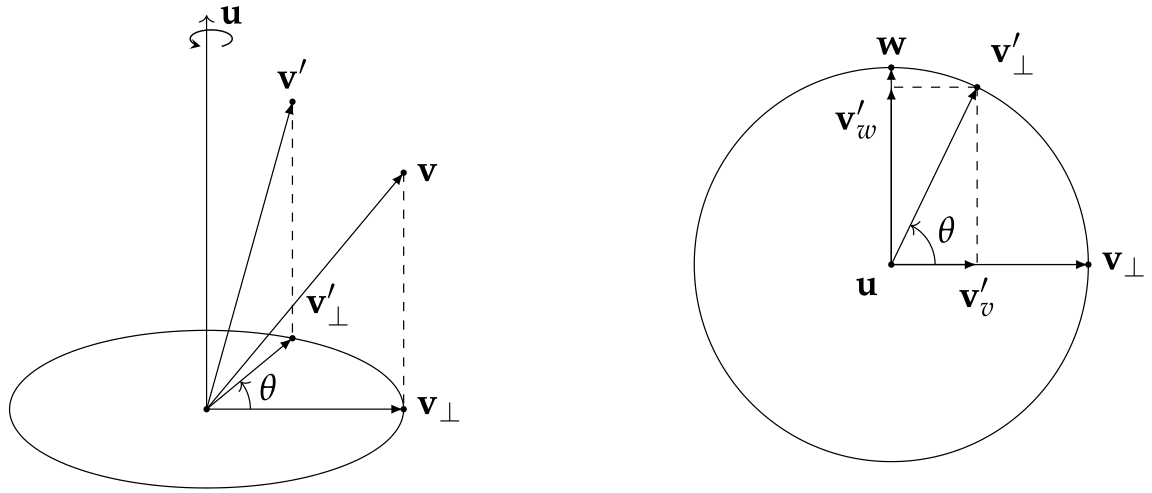
利用叉乘构造一个同时正交于 和 的向量 ,

$$\boldsymbol{w}=\boldsymbol{u}\times\boldsymbol{v}_{\perp}$$

已知 , 以及 与 夹角为 , 因此

$$\Vert\boldsymbol{w}\Vert =\Vert\boldsymbol{u}\times\boldsymbol{v}_{\perp}\Vert =\Vert\boldsymbol{u}\Vert\cdot\Vert\boldsymbol{v}_{\perp}\Vert =\Vert\boldsymbol{v}_{\perp}\Vert$$

即 与 共圆.

将 分别投影到 和 上作正交分解, 得到

$$\begin{align*} \boldsymbol{v}_{\perp}' &=\cos(\theta)\boldsymbol{v}_{\perp}+\sin(\theta)\boldsymbol{w}\\ &=\cos(\theta)\boldsymbol{v}_{\perp}+\sin(\boldsymbol{u}\times\boldsymbol{v}_{\perp})\tag{6} \end{align*}$$

4 空间向量的旋转

由式 (4, 5, 6) 得

$$\begin{align*} \boldsymbol{v}' &=\boldsymbol{v}_{\Vert}'+\boldsymbol{v}_{\perp}'\\ &=\boldsymbol{v}_{\Vert}'+\cos(\theta)\boldsymbol{v}_{\perp}+\sin(\theta)(\boldsymbol{u}\times\boldsymbol{v}_{\perp})\tag{7} \end{align*}$$

由

$$\begin{align*} \boldsymbol{u}\times\boldsymbol{v}_{\perp} &=\boldsymbol{u}\times(\boldsymbol{v}-\boldsymbol{v}_{\Vert})\\ &=\boldsymbol{u}\times\boldsymbol{v}-\boldsymbol{u}\times\boldsymbol{v}_{\Vert}\\ &=\boldsymbol{u}\times\boldsymbol{v} \end{align*}$$

最后将 (2, 3) 代入 (7), 即得, 三维空间中任一向量 绕单位向量 旋转 角度之后的 为

$$\begin{align*} \boldsymbol{v}' &=(\boldsymbol{u}\cdot\boldsymbol{v})\boldsymbol{u}+\cos(\theta)\left(\boldsymbol{v}-(\boldsymbol{u}\cdot\boldsymbol{v})\boldsymbol{u}\right)+\sin(\theta)(\boldsymbol{u}\times\boldsymbol{v})\\ &=\cos(\theta)\boldsymbol{v}+(1-\cos(\theta))(\boldsymbol{u}\cdot\boldsymbol{v})\boldsymbol{u}+\sin(\theta)(\boldsymbol{u}\times\boldsymbol{v}) \end{align*}$$

这就是著名的罗德里格旋转公式 (Rodrigues' Rotation Formula).

参考文献

1. Krasjet. 四元数与三维旋转. https://github.com/Krasjet/quaternion