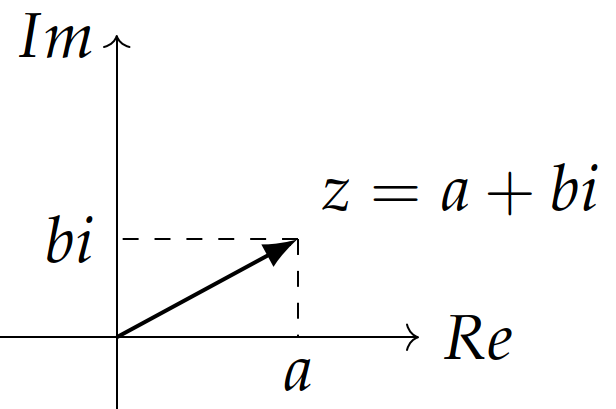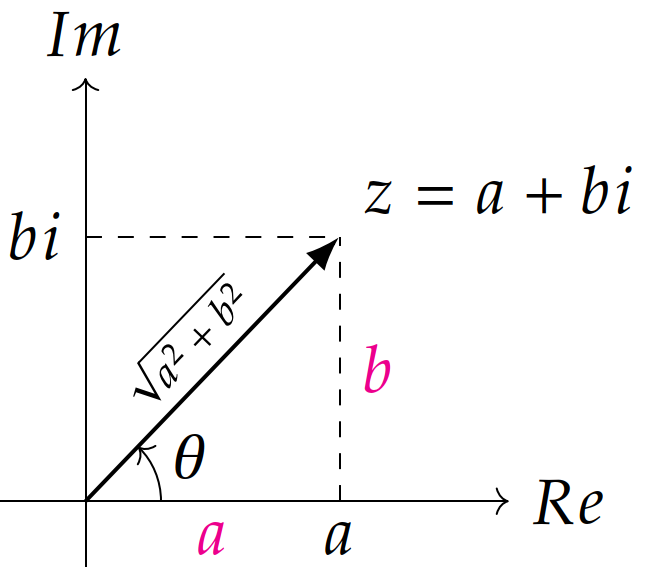本文主要整理自 Krasjet 的 "四元数与三维旋转" 第一章.

复数 (Complex Number) 与二维旋转的关系, 四元数 (Quaternion) 与三维旋转的关系, 二者非常相似, 因此有必要首先就前者进行讨论.

1 定义

定义形如 (其中 且 ) 的数叫做复数, 其中 称为虚数单位, 称为这个复数的实部 (Real Part), 称为这个复数的虚部 (Imaginary Part). 全体复数的集合叫做复数集, 记作 .

复数 即为关于基 (Basis) 的线性组合, 因此可以用向量表示为:

$$z=\begin{bmatrix}a\\b\end{bmatrix}$$

进一步可以在复平面中表示为一个点. 复平面中, 横坐标 代表复数的实部, 纵坐标 表示复数的虚部.

2 性质

2.1 复数乘法

对于两个复数 , , 它们的乘积可通过乘法分配律来计算:

$$\begin{align*} z_1z_2=&\space(a_1+b_1\mathrm{i})(a_2+b_2\mathrm{i})\\ =&\space a_1a_2+a_1b_2\mathrm{i}+b_1a_2\mathrm{i}+b_1b_2\mathrm{i}^2\\ =&\space(a_1a_2-b_1b_2)+(b_1a_2+a_1b_2)\mathrm{i}\\ =&\space(a_1{\color{red}{a_2}}-b_1{\color{green}{b_2}})+\\ &\space(b_1{\color{red}{a_2}}+a_1{\color{green}{b_2}})\mathrm{i} \end{align*}$$

仔细观察可以发现, 复数相乘的结果也可以是一个矩阵与向量相乘的结果:

$$z_1z_2= \begin{bmatrix} a_1&-b_1\\ b_1&a_1 \end{bmatrix} \begin{bmatrix} {\color{red}{a_2}}\\ {\color{green}{b_2}} \end{bmatrix}$$

右侧的 是向量形式表示的 , 而左侧的 则定义为 的矩阵形式, 这里记为 .

进一步, 若将复数乘法中的复数看作一种变换, 复数乘法便可在矩阵形式下转化为矩阵乘法.

注意, 复数乘法是满足交换律的. 容易验证, 以上矩阵与向量相乘的结果也可以写为:

$$[z_1]z_2 = \begin{bmatrix} a_1&-b_1\\ b_1&a_1 \end{bmatrix} \begin{bmatrix} {\color{red}{a_2}}\\ {\color{green}{b_2}} \end{bmatrix} = \begin{bmatrix} {\color{red}{a_2}}&-{\color{green}{b_2}}\\ {\color{green}{b_2}}&{\color{red}{a_2}} \end{bmatrix} \begin{bmatrix} a_1\\ b_1 \end{bmatrix} =[z_2]z_1$$

在矩阵形式下, 两个复数的乘积 所代表的变换同样满足交换律:

$$\begin{align*} [z_1z_2]&=\begin{bmatrix} a_1a_2-b_1b_2&-(b_1a_2+a_1b_2)\\ b_1a_2+a_1b_2&a_1a_2-b_1b_2 \end{bmatrix}\\ &= \begin{bmatrix} a_1&-b_1\\ b_1&a_1 \end{bmatrix} \begin{bmatrix} a_2&-b_2\\ b_2&a_2 \end{bmatrix} =[z_1][z_2]\\ &= \begin{bmatrix} a_2&-b_2\\ b_2&a_2 \end{bmatrix} \begin{bmatrix} a_1&-b_1\\ b_1&a_1 \end{bmatrix}=[z_2][z_1]\\ &=[z_2z_1] \end{align*}$$

因此, 我们可以将复数 与矩阵 建立等价关系. 进一步, 得到一些特殊复数的矩阵形式:

$$\begin{align*} [1]&=\begin{bmatrix}1&0\\0&1\end{bmatrix}=I & (a=1,b=0)\\ [\mathrm{i}]&=\begin{bmatrix}0&-1\\1&0\end{bmatrix} &(a=0,b=1) \end{align*}$$

可以验证

$$[\mathrm{i}^2]=[\mathrm{i}]\cdot[\mathrm{i}] =\begin{bmatrix}0&-1\\1&0\end{bmatrix}\begin{bmatrix}0&-1\\1&0\end{bmatrix} =\begin{bmatrix}-1&0\\0&-1\end{bmatrix} =-I=[-1]$$

即使在矩阵形式下, 与 也是等价的.

2.2 复数加减法

对于两个复数 , , 它们的和差即为对应分量相加减的结果:

$$\begin{align*} z_1+z_2&=(a_1+a_2)+(b_1+b_2)\mathrm{i}\\ z_1-z_2&=(a_1-a_2)+(b_1-b_2)\mathrm{i} \end{align*}$$

可以发现, 复数的矩阵形式在加减运算时也是成立的:

$$[z_1+z_2] =\begin{bmatrix}a_1+a_2&-(b_1+b_2)\\b_1+b_2&a_1+a_2\end{bmatrix} =\begin{bmatrix}a_1&-b_1\\b_1&a_1\end{bmatrix}+\begin{bmatrix}a_1&-b_1\\b_1&a_1\end{bmatrix} =[z_1]+[z_2]$$ $$[z_1-z_2] =\begin{bmatrix}a_1-a_2&-(b_1-b_2)\\b_1-b_2&a_1-a_2\end{bmatrix} =\begin{bmatrix}a_1&-b_1\\b_1&a_1\end{bmatrix}-\begin{bmatrix}a_1&-b_1\\b_1&a_1\end{bmatrix} =[z_1]-[z_2]$$

进而可以得到更一般的形式:

$$[z]=[a+b\mathrm{i}]=[a]+b[\mathrm{i}]$$

2.3 复数的模长与共轭

对于复数 , 复数的模长 (Magnitude) 定义为

$$\|z\|=\sqrt{a^2+b^2}$$

复数的共轭定义为

$$\bar{z}=a-b\mathrm{i}$$

注意到

$$\begin{align*} z\bar{z}&=(a+b\mathrm{i})(a-b\mathrm{i})\\ &=a^2+b^2\\ &=\|z\|^2 \end{align*}$$

因此可以通过与共轭乘积的方式来计算复数的模长.

对于矩阵形式的复数 , 其行列式恰好也等于复数的模长的平方:

$$\det\left([z]\right)=a^2+b^2=\|z\|^2$$

其转置也恰好对应复数共轭的矩阵形式:

$$[z]^T=\begin{bmatrix}a&b\\-b&a\end{bmatrix}=[\bar{z}]$$

进一步还能发现

$$[z\bar{z}] =\begin{bmatrix}a&-b\\b&a\end{bmatrix} \begin{bmatrix}a&b\\-b&a\end{bmatrix} =\begin{bmatrix}a^2+b^2&0\\0&a^2+b^2\end{bmatrix} =\left[\|z\|^2\right]$$

3 复数乘法与二维旋转

对于一个复数 , 既然复数乘法等价于矩阵形式 所作出的变换, 那这种变换有什么更直观的几何意义呢?

将矩阵做变形

$$\begin{bmatrix}a&-b\\b&a\end{bmatrix} =\sqrt{a^2-b^2} \begin{bmatrix}\frac{a}{\sqrt{a^2-b^2}}&\frac{-b}{\sqrt{a^2-b^2}}\\ \frac{b}{\sqrt{a^2-b^2}}&\frac{a}{\sqrt{a^2-b^2}}\end{bmatrix}$$

在复平面中, 复数模长为 , 若将复数与实数轴正方向的夹角记为 , 则恰有

$$\cos(\theta)=\frac{a}{\sqrt{a^2-b^2}}\qquad\sin(\theta)=\frac{b}{\sqrt{a^2-b^2}}$$

因此原矩阵可变形为

$$\begin{align*} \begin{bmatrix}a&-b\\b&a\end{bmatrix} &=\|z\|\begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\end{bmatrix}\\ &=\left[\|z\|\right]\begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\end{bmatrix} \end{align*}$$

原矩阵变形为两个矩阵的复合, 左边的 为缩放矩阵, 右边的 便是我们熟悉的二维旋转矩阵.

因此复数的乘法实际上是旋转与缩放变换的复合. 一个复数 与任意复数 相乘, 都会将 逆时针旋转 角度, 并将其缩放 倍. 这便是复数乘法所代表的几何意义.

注意, 这里的旋转矩阵 对应的复数形式为 .

根据欧拉公式 (Euler's Formula)

$$e^{\mathrm{i}\theta}=\cos(\theta)+\mathrm{i}\sin(\theta)$$

定义 , 可以将复数表示为极坐标形式

$$z=\|z\|(\cos(\theta)+\mathrm{i}\sin(\theta))=re^{\mathrm{i}\theta}$$

这样便可以通过一组缩放因子 和旋转角度 来定义一个复数, 而且更直观地体现了其旋转与缩放的性质.

因此, 若将平面中的向量 旋转 角度得到 , 有三种等价的旋转公式.

1. 直接通过旋转矩阵进行变换

   $$v'=\begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\end{bmatrix}v$$

2. 将向量看作一个复数 , 使用复数相乘

   $$v'=(cos(\theta)+\mathrm{i}\sin(\theta))v$$

3. 将向量看作一个复数 , 使用极坐标形式的复数相乘

   $$v'=e^{\mathrm{i}\theta}v$$

参考文献

1. Krasjet. 四元数与三维旋转. https://github.com/Krasjet/quaternion
2. invo. 复数的矩阵表示. https://www.cnblogs.com/invo/p/18243532