本文为书籍 Introduction to Humanoid Robotics 的汉化, 主要借助翻译器 DeepL.

另外, 原书有管贻生教授的译作版本:《仿人机器人》(清华大学出版社, 2007年). 强烈推荐.

---

6 动力学仿真 (Dynamic Simulation)

图 6.1 展示了仿人机器人 HRP-2P 的摔倒实验. 通过进行动态模拟, 我们可以在实际进行此类实验之前预测机器人何时会落地以及落地的力度. 这也是一种强大的工具, 可用于开发摔倒控制方法, 以最大限度地减少触地冲击力, 并开发耐用的硬件.

本章旨在展示动态模拟的理论和实践. 首先, 我们将推导一个旋转物体在零重力空间中的运动方程. 通过开发该问题的模拟器, 我们将对动态模拟有一个直观的了解. 在接下来的章节中, 我们将通过引入平移, 重力和与环境的接触力来开发一个完整的刚体模拟器. 我们的技术模拟了一个旋转的陀螺, 这是令人印象深刻的三维动态运动之一.

机器人的动态模拟可以表述为由关节连接的多个刚体. 在本章末尾, 我们将概述 Featherstone 开发的一种高效算法.

6.1 旋转刚体的动力学

我们首先推导刚体绕其质心旋转的运动方程, 然后解释基于该方程的模拟程序. 在本节中, 我们假设刚体的质心静止在世界坐标系原点处.

6.1.1 欧拉运动方程

让我们回顾一下第 3 章学到的动力学基础知识. 物体的动量 在外加力向量 的作用下发生变化: . 将动量 的定义代入, 我们可以得到牛顿运动方程

$$\boldsymbol{f}=\frac{d}{dt}\mathcal{P}\quad\Rightarrow\quad\boldsymbol{f}=m\ddot{\boldsymbol{p}}.$$

同样, 物体的角动量 也会随着外加力矩的变化而变化

$$\boldsymbol{\tau}=\frac{d}{dt}\mathcal{L}.\tag{6.1}$$

在给定角速度向量 和惯性张量 的情况下, 刚体的角动量计算公式为

$$\mathcal{L}=\boldsymbol{I}\boldsymbol{\omega}.\tag{6.2}$$

朝向 的刚体的惯性张量为

$$\boldsymbol{I}=\boldsymbol{R}\bar{\boldsymbol{I}}\boldsymbol{R}^T,\tag{6.3}$$

其中, 是标准姿态下的惯性张量.

这些就是我们在第 3 章学到的内容.

现在我们可以推导出刚体的旋转方程. 将 (6.2) 和 (6.3) 代入 (6.1), 我们得到

$$\begin{align*} \boldsymbol{\tau} &=\frac{d}{dt}(\boldsymbol{R}\bar{\boldsymbol{I}}\boldsymbol{R}^T\boldsymbol{\omega})\\ &=\dot{\boldsymbol{R}}\bar{\boldsymbol{I}}\boldsymbol{R}^T\boldsymbol{\omega}+\boldsymbol{R}\bar{\boldsymbol{I}}\dot{\boldsymbol{R}}^T\boldsymbol{\omega}+\boldsymbol{R}\bar{\boldsymbol{I}}\boldsymbol{R}^T\dot{\boldsymbol{\omega}}. \end{align*}$$

利用旋转基本方程 ,

$$\boldsymbol{\tau}=\boldsymbol{\omega}\times(\boldsymbol{R}\bar{\boldsymbol{I}}\boldsymbol{R}^T\boldsymbol{\omega})+(\boldsymbol{R}\bar{\boldsymbol{I}}\boldsymbol{R}^T)\dot{\boldsymbol{\omega}}.$$

最后, 用 (6.3) 代替惯性张量, 我们就得到了下式, 即欧拉方程

$$\boldsymbol{\tau}=\boldsymbol{I}\dot{\boldsymbol{\omega}}+\boldsymbol{\omega}\times\boldsymbol{I}\boldsymbol{\omega}.\tag{6.4}$$

6.1.2 刚体旋转仿真

欧拉方程比牛顿方程复杂一些. 为了理解其本质, 让我们做一个简单的仿真.

假设一个尺寸为 0.1 0.4 0.9 [] 的长方体在零重力空间围绕质心自由旋转. 角速度 的变化基于欧拉方程 (6.4), 而其姿态 的变化则基于第 2 章中的旋转方程 (2.33)

$$\dot{\boldsymbol{\omega}}=-\boldsymbol{I}^{-1}(\boldsymbol{\omega}\times\boldsymbol{I}\boldsymbol{\omega})\tag{6.5},$$ $$\dot{\boldsymbol{R}}=\hat{\boldsymbol{\omega}}\boldsymbol{R}.\tag{6.6}$$

假定角加速度和速度 在短时间 内保持不变, 我们可以对这些微分方程进行数值积分, 计算公式为

$$\left\{\begin{align*} &\boldsymbol{\omega}(t+\Delta t)=\boldsymbol{\omega}(t)+\dot{\boldsymbol{\omega}}\Delta t,\\ &\boldsymbol{R}(t+\Delta t)=e^{\hat{\boldsymbol{\omega}}\Delta t}\boldsymbol{R}(t). \end{align*}\right.$$

仿真结果如图 6.2 所示. 在没有外力作用的情况下, 我们看到物体以一种复杂的方式旋转. 图 6.3 的上图显示了角速度从初始值 开始的变化 (rad/s) . 另一方面, 图 6.3 下图所示的角动量保持不变. 这表明角动量守恒是意料之中的, 仿真也是有效的.

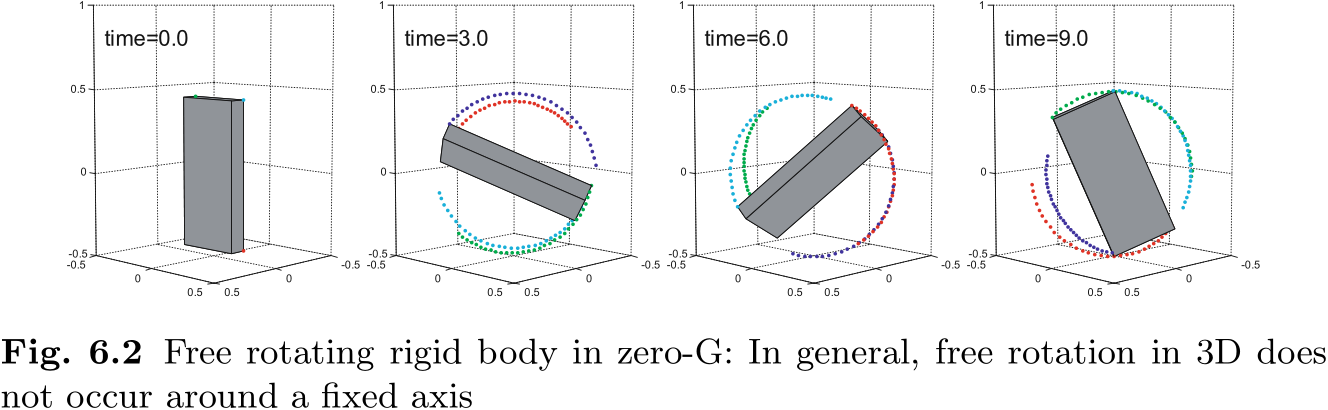
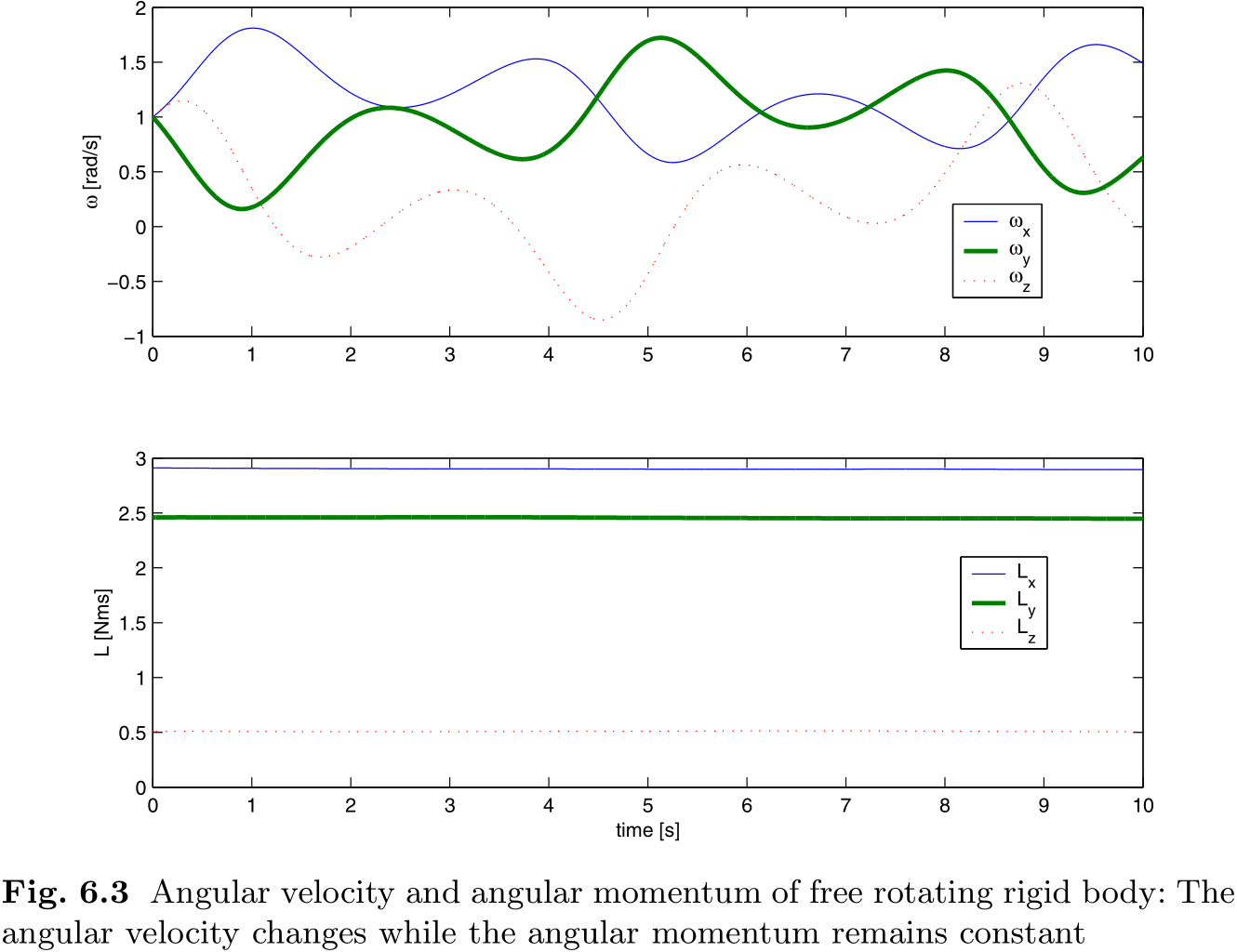
就像这次仿真一样, 一般来说, 三维空间中的浮动刚体旋转方式比较复杂, 没有固定的旋转轴. 角速度的变化由 (6.5) 给出, 在外部力矩为零的情况下, 角加速度不为零. 角加速度的来源是惯性张量的变化, 即旋转引起的质量分布的变动.

我们可能需要利用这种旋转来清理环绕地球运行的太空碎片, 这些碎片可能会对未来的太空飞船造成伤害.

图 6.4 和 6.5 显示了仿真旋转物体的 Matlab 代码.

• 图 6.4 EulerDynamics.m 计算欧拉方程

  1 2 3 4 5

  function L = EulerDynamics(j) global uLINK I = uLINK(j).R * uLINK(j).I * uLINK(j).R'; % Inertia tensor L = I * uLINK(j).w; % Angular momentum uLINK(j).dw = I(-cross(uLINK(j).w, L)); % Euler's equation

• 图 6.5 自由刚体旋转的模拟代码. 有关 MakeRigidBody 和 ShowObject 子程序, 请参见第 6.6.2 节.

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  global uLINK lx = 0.1; ly = 0.4; lz = 0.9; % Depth, Width, Height [m] mass = 36.0; % Mass [kg] MakeRigidBody(1, [lx ly lz], mass);% Create rigid body uLINK.p = [0.0, 0.0, 0]'; % Initial position [m] uLINK.R = eye(3); % Initial posture uLINK.w = [1, 1, 1]'; % Initial angular velocity [rad/s] Dtime = 0.02; % Integration time [s] EndTime = 5.0; % End of simulation [s] time = 0:Dtime:EndTime; figure AX = [-0.5 0.5]; AY = [-0.5 0.5]; AZ = [-0.5 1.0]; % 3D view area for n = 1:length(time) L = EulerDynamics(1); % Euler's equation uLINK(1).R = Rodrigues(uLINK(1).w, Dtime) * uLINK(1).R; % Rodrigues uLINK(1).w = uLINK(1).w + Dtime * uLINK(1).dw; % Euler-method ShowObject; % Show object end

6.2 空间速度

6.2.1 刚体速度

在机器人学中, 我们使用两种不同的方法来表示刚体在三维空间中的平移速度.

• (A) 参考点速度: 在刚体上设置一个适当的参考点 (如质心或关节中心) , 则其在世界坐标系中的速度 被视为刚体的速度. 对于参考点 的位置, 刚体上任意点 的速度取值为

  $$\boldsymbol{v}(\boldsymbol{p})=\boldsymbol{v}_1+\boldsymbol{\omega}\times(\boldsymbol{p}-\boldsymbol{p}_1).$$

• (B) 空间速度: 以下向量被视为刚体的平移速度 [30]

  $$\boldsymbol{v}_o=\boldsymbol{v}_1-\boldsymbol{\omega}\times\boldsymbol{p}_1.\tag{6.7}$$
  

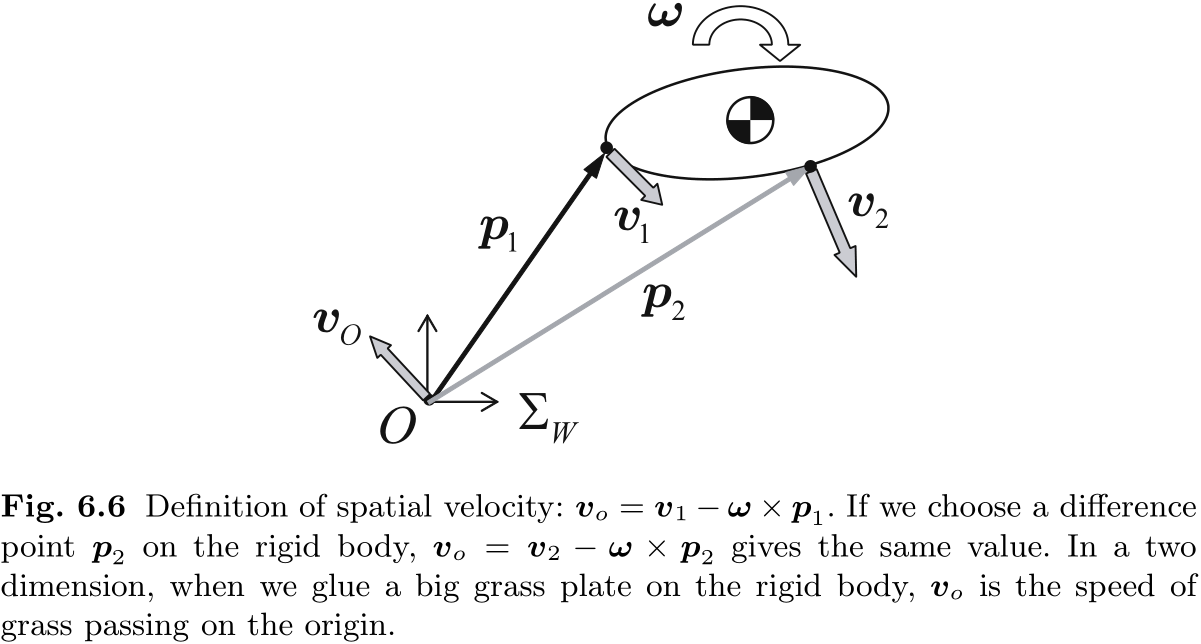
  如图 6.6 所示, 在给定的刚体瞬时状态下, 无论 如何选择, 我们都能得到唯一的 . 因此, 我们可以将 视为刚体的固有平移速度. 在世界坐标系中, 以速度 运动的刚体上的点 的速度由以下公式给出

  $$\boldsymbol{v}(\boldsymbol{p})=\boldsymbol{v}_o+\boldsymbol{\omega}\times\boldsymbol{p}.\tag{6.8}$$

  由 组成的六维向量称为刚体的空间速度[30, 101].

通常, 刚体的平移速度用 (A) 表示. 事实上, 在第 2 章中, 我们以局部坐标系原点为参考点, 用 (A) 定义了平移速度.

另一方面, 通过使用 (B) 中的空间速度, 加速度的处理大大简化, 并最终实现了本节末将讨论的 Featherstone 快速动力学计算. 因此, 我们使用 (B) 中描述的方法来表示刚体运动.

6.2.2 整合空间速度

在本节中, 我们将解释一种通过对给定的空间速度进行积分来更新位置和朝向的方法. 不幸的是, 这种计算方法有点复杂. 让我们将给出以空间速度 运动的刚体上点 的速度的 (6.8) 重写为

$$\begin{bmatrix}\dot{\boldsymbol{p}}\\0\end{bmatrix} =\begin{bmatrix}\hat{\boldsymbol{\omega}}&\boldsymbol{v}_o\\0\enspace0\enspace0&0\end{bmatrix}\begin{bmatrix}\boldsymbol{p}\\1\end{bmatrix}=\boldsymbol{\Xi}\begin{bmatrix}\boldsymbol{p}\\1\end{bmatrix}\tag{6.9}$$

其中, 是一个 矩阵, 定义为

$$\boldsymbol{\Xi}\equiv\begin{bmatrix}\hat{\boldsymbol{\omega}}&\boldsymbol{v}_o\\0\enspace0\enspace0&0\end{bmatrix}.$$

如果 为常数, 微分方程 (6.9) 的解则为

$$\begin{bmatrix}\boldsymbol{p}(t)\\1\end{bmatrix}=e^{\boldsymbol{\Xi}t}\begin{bmatrix}\boldsymbol{p}(0)\\1\end{bmatrix}.\tag{6.10}$$

矩阵指数 是由无穷级数定义的, 就像第 2 章所示的旋转矩阵一样

$$e^{\boldsymbol{\Xi}t}=\boldsymbol{E}+\boldsymbol{\Xi}t+\frac{(\boldsymbol{\Xi}t)^2}{2!}+\frac{(\boldsymbol{\Xi}t)^3}{3!}+\dots\quad.\tag{6.11}$$

为了简化这个无穷级数, 我们首先对空间速度进行归一化处理, 使角速度的范数变为 1

$$\begin{align*} \boldsymbol{\omega}_n&=\boldsymbol{\omega}/\|\boldsymbol{\omega}\|\\ \boldsymbol{v}_{on}&=\boldsymbol{v}_o/\|\boldsymbol{\omega}\|\\ t'&=\|\boldsymbol{\omega}\|t. \end{align*}$$

由此, 我们可以得出以下方程

$$e^{\boldsymbol{\Xi}t}=\begin{bmatrix} e^{\hat{\boldsymbol{\omega}}_nt'}(\boldsymbol{E}-e^{\hat{\boldsymbol{\omega}}_nt'})&(\boldsymbol{\omega}_n\times\boldsymbol{v}_{on})+\boldsymbol{\omega}_n\boldsymbol{\omega}_n^T\boldsymbol{v}_{on}t'\\ 0\enspace0\enspace0 & 1 \end{bmatrix}.\tag{6.12}$$

更详细的推导, 请参见 Murray, Li 和 Sastry 的教科书[101] (第 39-42 页) .

如果角速度 为零, 我们就无法对空间速度进行归一化处理. 然而, 这种情况下只需平移而无需旋转, 因此我们可以得到

$$e^{\boldsymbol{\Xi}t}=\begin{bmatrix}\boldsymbol{E} &\boldsymbol{v}_{o}t\\ 0\enspace0\enspace0 & 1 \end{bmatrix}.\tag{6.13}$$

当刚体在时间 时的位置和朝向为 , 其空间速度为 时, 其在 时的参数由以下公式给出

$$\begin{bmatrix} \boldsymbol{R}(t+\Delta t)&\boldsymbol{p}(t+\Delta t)\\ 0\enspace0\enspace0&1 \end{bmatrix}=e^{\boldsymbol{\Xi}\Delta t}\begin{bmatrix} \boldsymbol{R}(t)&\boldsymbol{p}(t)\\ 0\enspace0\enspace0&1 \end{bmatrix}.\tag{6.14}$$

方程 (6.12), (6.13) 和 (6.14) 可以编码成 Matlab 程序, 如图 6.7 所示. 程序中引入了一个新变量 uLINK.vo, 用于保存空间速度的线性部分 .

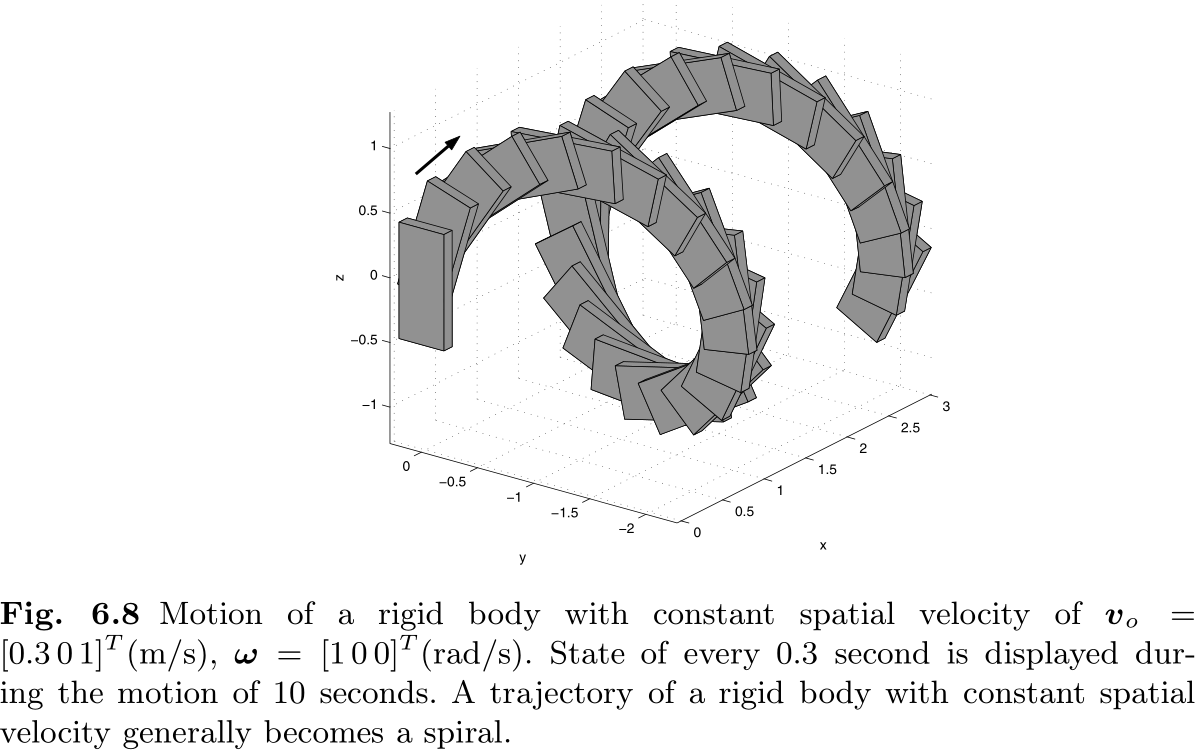
图 6.8 显示了图 6.7 所示程序计算出的刚体在恒定空间速度下的运动情况.

• 图 6.7 SE3exp.m 根据空间速度更新位置和朝向

  1 2 3 4 5 6 7 8 9 10 11 12 13 14

  function [p2, R2] = SE3exp(j, dt) global uLINK norm_w = norm(uLINK(j).w); if norm_w < eps p2 = uLINK(j).p + dt * uLINK(j).vo; R2 = uLINK(j).R; else th = norm_w*dt; wn = uLINK(j).w/norm_w; % normalized vector vo = uLINK(j).vo/norm_w; rot = Rodrigues(wn, th); p2 = rot * uLINK(j).p +(eye(3)-rot)*cross(wn, vo) + wn * wn' * vo * th; R2 = rot * uLINK(j).R; end

6.3 刚体动力学

本节将讨论三维空间中刚体的动力学和仿真方法.

6.3.1 牛顿-欧拉方程

众所周知, 刚体动力学可分为质心 (CoM) 的平移和围绕质心的旋转. 因此, 三维空间中的刚体动力学由质心的牛顿方程和围绕质心的欧拉方程给出. 这些方程称为牛顿-欧拉方程, 其式如下

$$\boldsymbol{f}=m\ddot{\boldsymbol{c}},\tag{6.15}$$ $$\boldsymbol{\tau}^{(c)}=\boldsymbol{I}\dot{\boldsymbol{\omega}}+\boldsymbol{\omega}\times\boldsymbol{I}\boldsymbol{\omega},\tag{6.16}$$

其中, 是作用在 CoM 上的外部线性力, 是刚体的质量, 是 CoM 相对于世界坐标系的位置. 是 CoM 周围的外力矩, 是世界坐标系中的惯性张量和角速度.

6.3.2 空间速度的动力学

让我们用空间速度重写牛顿-欧拉方程. 假设我们有一个刚体, 其 CoM 速度为 , 旋转速度为 .

$$\boldsymbol{v}_o=\dot{\boldsymbol{c}}-\boldsymbol{\omega}\times\boldsymbol{c}.\tag{6.17}$$

求导得

$$\dot{\boldsymbol{v}}_o=\ddot{\boldsymbol{c}}-\dot{\boldsymbol{\omega}}\times\boldsymbol{c}-\boldsymbol{\omega}\times\dot{\boldsymbol{c}}.\tag{6.18}$$

由 (6.18) 和 (6.17) 可得, CoM 的加速度为

$$\ddot{\boldsymbol{c}}=\dot{\boldsymbol{v}}_o-\boldsymbol{c}\times\dot{\boldsymbol{\omega}}+\boldsymbol{\omega}\times(\boldsymbol{v}_o+\boldsymbol{\omega}\times\boldsymbol{c}).\tag{6.19}$$

将其代入牛顿方程 (6.15), 我们就得到了空间速度表示下的平移运动方程

$$\boldsymbol{f}=m\left(\dot{\boldsymbol{v}}_o-\boldsymbol{c}\times\dot{\boldsymbol{\omega}}+\boldsymbol{\omega}\times(\boldsymbol{v}_o+\boldsymbol{\omega}\times\boldsymbol{c})\right).\tag{6.20}$$

另一方面, 作用在惯性体上的力 和惯性体周围的力矩 会产生世界坐标系原点周围的力矩, 即

$$\boldsymbol{\tau}=\boldsymbol{\tau}^{c}+\boldsymbol{c}\times\boldsymbol{f}.\tag{6.21}$$

将欧拉方程 (6.16) 和 (6.20) 代入 (6.21), 我们可以得到空间速度表示下的旋转动力学方程

$$\boldsymbol{\tau}=\boldsymbol{I}\dot{\boldsymbol{\omega}}+\boldsymbol{\omega}\times\boldsymbol{I}\boldsymbol{\omega}+m\boldsymbol{c}\times\left(\dot{\boldsymbol{v}}_o-\boldsymbol{c}\times\dot{\boldsymbol{\omega}}+\boldsymbol{\omega}\times(\boldsymbol{v}_o+\boldsymbol{\omega}\times\boldsymbol{c})\right).\tag{6.22}$$

(6.20) 和 (6.22) 这两个看起来令人讨厌的方程式可以组织成下面的矩阵方程. 这是使用空间速度的刚体运动方程

$$\begin{bmatrix} \boldsymbol{f}\\ \boldsymbol{\tau} \end{bmatrix}=\boldsymbol{I}^S\begin{bmatrix} \dot{\boldsymbol{v}}_o\\ \dot{\boldsymbol{\omega}} \end{bmatrix}+\begin{bmatrix} \hat{\boldsymbol{\omega}}&\boldsymbol{0}\\ \hat{\boldsymbol{v}}_o&\hat{\boldsymbol{\omega}}\end{bmatrix}\boldsymbol{I}^S\begin{bmatrix} \boldsymbol{v}_o\\ \boldsymbol{\omega} \end{bmatrix}.\tag{6.23}$$

矩阵 是一个 对称矩阵, 由以下方程定义, 称为空间惯性矩阵

$$\boldsymbol{I}^S\equiv\begin{bmatrix}m\boldsymbol{E}&m\hat{\boldsymbol{c}}^T\\m\hat{\boldsymbol{c}}&m\hat{\boldsymbol{c}}\hat{\boldsymbol{c}}^T+\boldsymbol{I}\end{bmatrix}.\tag{6.24}$$

此外, 六维向量 也被称为空间加速度.

注意, 刚体的动量和角动量计算公式为

$$\begin{bmatrix}\mathcal{P}\\ \mathcal{L}\end{bmatrix}=\boldsymbol{I}^S\begin{bmatrix}\boldsymbol{v}_o\\ \boldsymbol{\omega}\end{bmatrix}.\tag{6.25}$$

6.3.3 基于空间速度的刚体仿真

通过使用空间速度的刚体运动方程 (6.23), 我们可以计算出在给定力和力矩 作用下的空间加速度, 计算公式为

$$\begin{bmatrix} \dot{\boldsymbol{v}}_o\\ \dot{\boldsymbol{\omega}} \end{bmatrix} =(\boldsymbol{I}^S)^{-1}\left( \begin{bmatrix} \boldsymbol{f}\\ \boldsymbol{\tau} \end{bmatrix}-\begin{bmatrix} \hat{\boldsymbol{\omega}}&\boldsymbol{0}\\ \hat{\boldsymbol{v}}_o&\hat{\boldsymbol{\omega}}\end{bmatrix}\boldsymbol{I}^S\begin{bmatrix} \boldsymbol{v}_o\\ \boldsymbol{\omega} \end{bmatrix}\right).\tag{6.26}$$

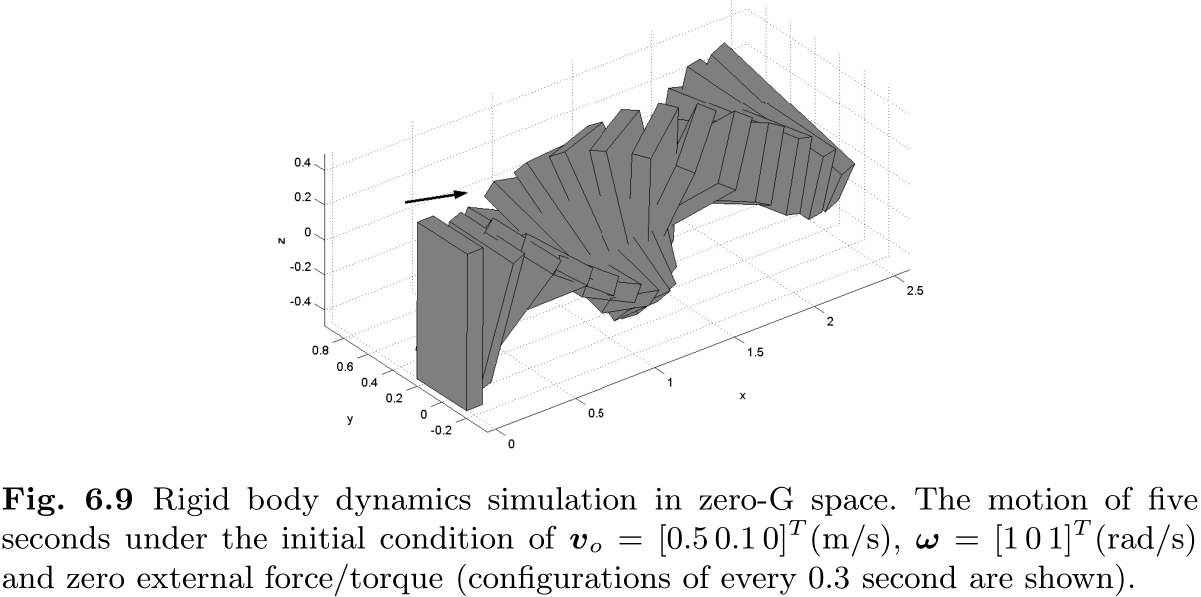
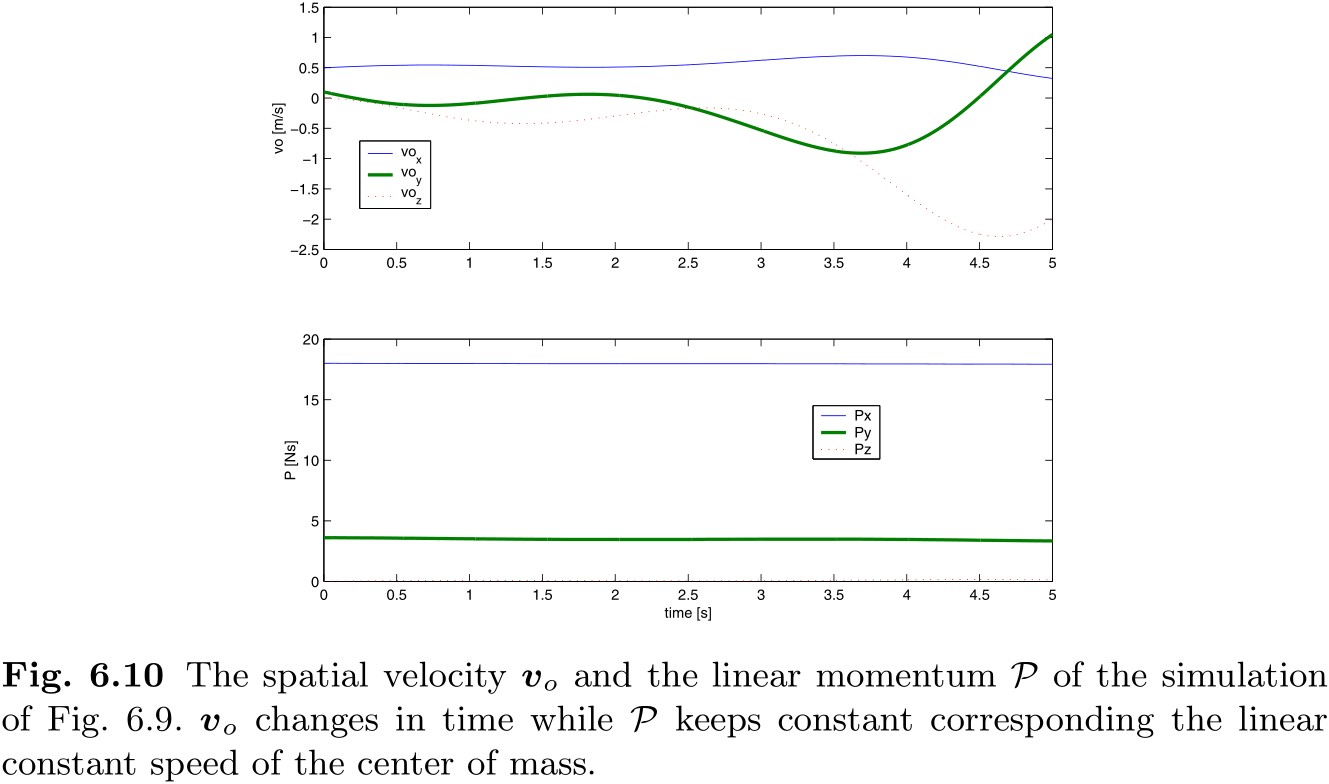
图 6.9 显示了根据该方程 对零重力空间中浮动刚体的仿真结果. 物体的质心以 6.1.2 节中观察到的自由旋转方式匀速运动.

仿真的空间速度 和线性动量如图 6.10 所示. 虽然 CoM 的速度是恒定的, 但由于物体的旋转, 空间速度 会随时间变化. 当然, 线动量保持不变.

与其使用空间速度和 (6.26), 有些人可能更喜欢使用原始的牛顿-欧拉方程 (6.15) 和 (6.16) 来进行此类单刚体仿真. 尽管如此, 请耐心等待第 6.4 节, 在该节中, 多体系统的计算将显示空间速度表示法的优势.

图 6.11 列出了部分用于仿真的 Matlab 代码. 引入了一个新变量 uLINK.dvo, 用于保存空间加速度 .

• 图 6.11 SE3dynamics.m 刚体运动方程

  1 2 3 4 5 6 7 8 9 10 11 12 13 14

  function [P,L] = SE3dynamics(j) global uLINK w_c = uLINK(j).R * uLINK(j).c + uLINK(j).p; % Center of mass w_I = uLINK(j).R * uLINK(j).I * uLINK(j).R'; % Inertia tensor c_hat = wedge(w_c); Iww = w_I + uLINK(j).m * c_hat * c_hat'; Ivv = uLINK(j).m * eye(3); Iwv = uLINK(j).m * c_hat; P = uLINK(j).m * (uLINK(j).vo + cross(uLINK(j).w,w_c)); % Lin. momentum L = uLINK(j).m * cross(w_c,uLINK(j).vo) + Iww * uLINK(j).w; % Ang. momentum pp = [cross(uLINK(j).w,P); cross(uLINK(j).vo,P) + cross(uLINK(j).w,L)]; a0 = -[Ivv, Iwv'; Iwv, Iww] pp; % Spatial acceleration uLINK(j).dvo = a0(1:3); uLINK(j).dw = a0(4:6);

6.3.4 陀螺仿真

基于以上讨论, 让我们仿真一个旋转的陀螺, 它在三维空间中表现出刚体的一种非常有趣的行为.

作用在陀螺上的力有 (1) CoM 上的重力 和 (2) 作用在陀螺底部的地板反作用力. 第一个力为

$$\boldsymbol{f}_g=\begin{bmatrix}0&0&-mg\end{bmatrix}^T.$$

第二个力只在陀螺位于地面上时才起作用. 其垂直分力可以通过弹簧-阻尼系统计算, 水平摩擦力可以通过以下方法计算

$$\boldsymbol{f}_c=\left\{ \begin{align*} &\begin{bmatrix}-D_f\dot{p}_x & -D_f\dot{p}_y & -K_fp_z-D_f\dot{p}_z\end{bmatrix}^T &(\text{if }p_z<0)\\ &\begin{bmatrix}0&0&0\end{bmatrix}^T &(\text{if }p_z>0) \end{align*}\right.$$

其中, 是陀螺的底部. 是阻尼系数, 是弹簧系数, 表示地板刚度.

这些力在世界坐标系原点周围产生的力矩 为

$$\boldsymbol{\tau}=\boldsymbol{c}\times\boldsymbol{f}_g+\boldsymbol{p}\times\boldsymbol{f}_c.$$

有关计算的更多信息, 请参见第 6.6.1 节.

上述力的产生过程如图 6.12 所示.

• 图 6.12 TopForce.m: 作用在陀螺上的力和力矩

  1 2 3 4 5 6 7 8 9 10 11

  function [f,t] = TopForce(j) global uLINK G Kf Df w_c = uLINK(j).R * uLINK(j).c + uLINK(j).p; % center of mass f = [0 0 -uLINK(j).m * G]'; % gravity t = cross(w_c, f); % gravity moment around the origin if uLINK(j).p(3) < 0.0 % the top is contacting v = uLINK(j).vo + cross(uLINK(j).w,uLINK(j).p); % contacting speed fc = [-Df*v(1) -Df*v(2) -Kf*uLINK(j).p(3)-Df*v(3)]'; f = f + fc; t = t + cross(uLINK(j).p, fc); end

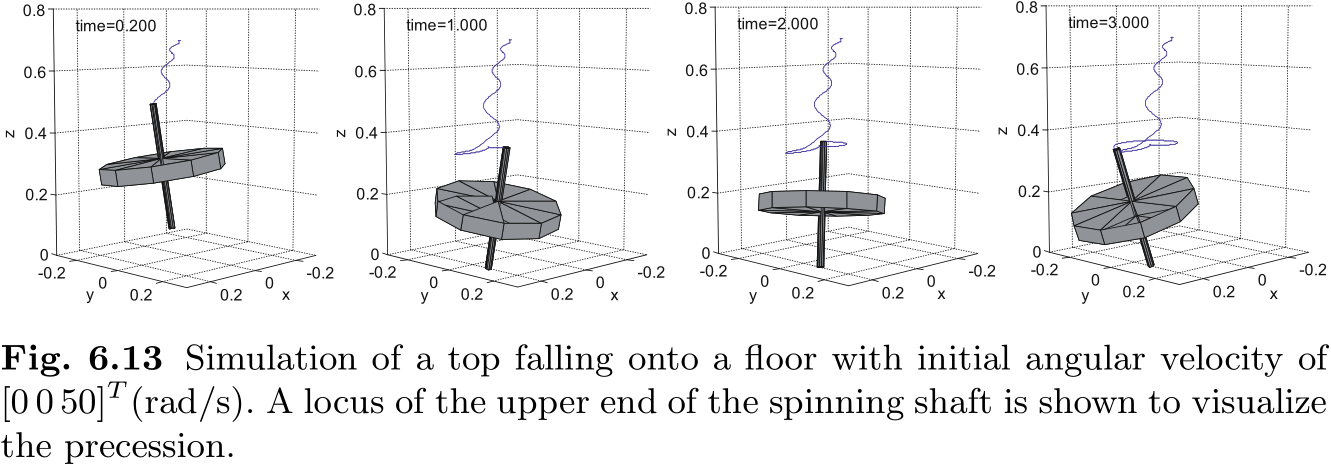
以适当的初始角速度模拟陀螺在 1G 重力下下落的情况如图 6.13 所示. 我们可以观察到旋转轴上端以圆周运动的形式出现的偏振.

仿真代码如图 6.14 所示. 空间加速度通过 (6.26) 计算, 空间速度通过以下方式更新

$$\left\{\begin{align*} &\boldsymbol{v}_o(t+\Delta t)=\boldsymbol{v}_o(t)+\dot{\boldsymbol{v}}_o\Delta t\\ &\boldsymbol{\omega}(t+\Delta t)=\boldsymbol{\omega}(t)+\dot{\boldsymbol{\omega}}\Delta t. \end{align*}\right.$$

• 图 6.14 仿真旋转陀螺的 Matlab 代码. 它还显示了仿真陀螺的动画效果. 有关 MakeTop 和 ShowObject 子程序, 请参见第 6.6.2 节.

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  global uLINK G Kf Df G = 9.8; Kf = 1.0E+4; Df = 1.0E+3; % Floor stiffness[N/m] viscosity[N/(m/s)] r = 0.2; a = 0.05; c = 0.2; % Top radius, thickness, shaft length/2 [m] MakeTop(1, r,a,c); uLINK(1).p = [0 0 0.3]'; % Initial position [m] uLINK(1).R = Rodrigues([1 0 0],pi/50); % Initial posture uLINK(1).vo = [0 0 0]'; % Initial speed [m/s] uLINK(1).w = [0 0 50]'; % Initial spin [rad/s] Dtime = 0.002; EndTime = 2.0; time = 0:Dtime:EndTime; figure frame_skip = 3; AX=[-0.2 0.4]; AY=[-0.3 0.3]; AZ=[0 0.8]; % 3D view area for n = 1:length(time) [f,tau] = TopForce(1); % External force [P,L] = SE3dynamics(1,f,tau); % Acceleration [uLINK.p, uLINK.R] = SE3exp(1, Dtime); % Update configuration uLINK(1).w = uLINK(1).w + Dtime * uLINK(1).dw; % Update ang. velocity uLINK(1).vo = uLINK(1).vo + Dtime * uLINK(1).dvo; % Update lin. velocity if mod(n,frame_skip) == 0 ShowObject; % Show the top end end

根据 (6.14) 使用图 6.7 中的程序更新陀螺的位置和朝向. 同时显示计算出的陀螺运动.

6.4 链节系统的动力学

在本节中, 我们将仿人机器人视为由多个刚体组成的链节系统, 对其动力学进行研究. 由于每个刚体的行为如上所述, 我们可以通过对它们进行一致的积分来获得整个系统的动力学特性.

6.4.1 带加速度的正向运动学

首先, 我们研究了由一个关节连接的一对刚体, 它代表了仿人机器人的最小元素.

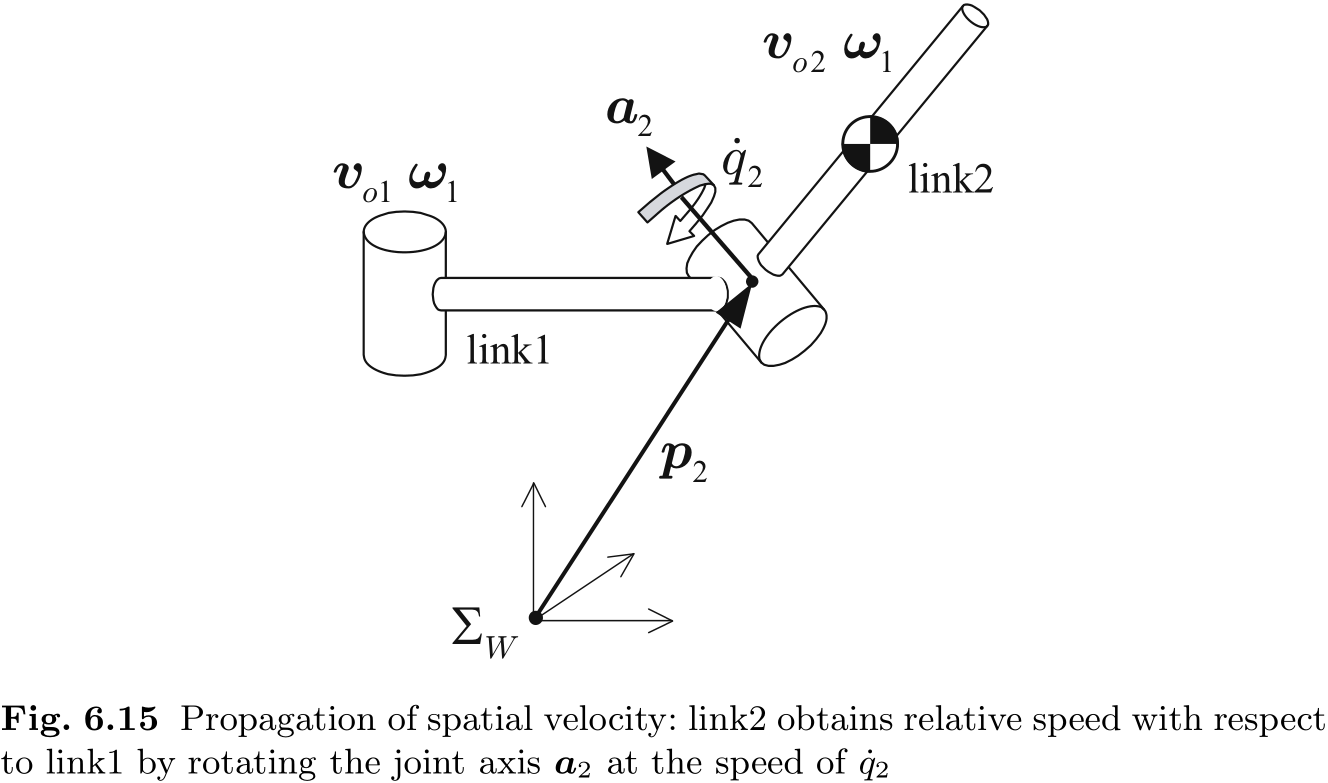
假设空间中的链节 1 通过旋转接头与链节 2 相连, 如图 6.15 所示. 当链节 1 静止时, 以 的速度转动关节 , 链节 2 的角速度为

$$\boldsymbol{\omega}_2=\boldsymbol{a}_2\dot{q}_2.\tag{6.27}$$

在第 6.2 节的空间速度表示法中, 链节 2 的线速度为

$$\boldsymbol{v}_{o2}=\dot{\boldsymbol{p}}_2-\boldsymbol{\omega}_2\times\boldsymbol{p}_2.$$

其中 是链节 2 的原点.

由于我们假设链节 1 是静止的, 因此 . 将 (6.27) 代入上式, 可得

$$\boldsymbol{v}_{o2}=\boldsymbol{p}_2\times\boldsymbol{a}_2\dot{q}_2.\tag{6.28}$$

公式 (6.28) 和 (6.27) 给出了链节 2 相对于链节 1 的相对速度 .

当链节 1 具有空间速度 时, 我们只需将其相加, 链节 2 的空间速度就变成了

$$\begin{bmatrix} \boldsymbol{v}_{o2}\\ \boldsymbol{\omega}_2 \end{bmatrix}=\begin{bmatrix} \boldsymbol{v}_{o1}\\ \boldsymbol{\omega}_1 \end{bmatrix}+\begin{bmatrix} \boldsymbol{p}_{2}\times\boldsymbol{a}_2\\ \boldsymbol{a}_2 \end{bmatrix}\dot{q}_2.\tag{6.29}$$

下面, 我们使用以下符号来简化方程

$$\boldsymbol{\xi}_2=\boldsymbol{\xi}_1+\boldsymbol{s}_2\dot{q}_2.\tag{6.30}$$ $$\boldsymbol{\xi}_j\equiv\begin{bmatrix}\boldsymbol{v}_{oj}\\ \boldsymbol{\omega}_j\end{bmatrix},\boldsymbol{s}_j\equiv\begin{bmatrix}\boldsymbol{p}_{j}\times\boldsymbol{a}_{j}\\ \boldsymbol{a}_j\end{bmatrix}$$

其中, 是空间速度, 是单位速度由关节旋转产生的空间速度. 它们都是六维向量.

通过求导 (6.30), 我们可以得到空间加速度的传播规则

$$\dot{\boldsymbol{\xi}}_2=\dot{\boldsymbol{\xi}}_1+\dot{\boldsymbol{s}}_2\dot{q}_2+\boldsymbol{s}_2\ddot{q}_2.\tag{6.31}$$

其中 的计算方法如下

$$\dot{\boldsymbol{s}}_2=\begin{bmatrix} \hat{\boldsymbol{\omega}}_1&\hat{\boldsymbol{v}}_{o1}\\ \boldsymbol{0}&\hat{\boldsymbol{\omega}}_1 \end{bmatrix}\boldsymbol{s}_2.\tag{6.32}$$

由于采用了空间速度表示法, 我们可以得到这个简单的方程. 当我们使用参考点的常规速度时, 我们需要更复杂的加速度传播规则[99].

假设我们知道机器人躯干的位置和朝向, 空间速度和空间加速度. 那么, 如果所有关节的角度, 速度和加速度也已知, 我们就可以通过应用 (6.30) 和 (6.31) 计算所有链节的空间速度和空间加速度, 即从躯干向四肢末端计算. 如图 6.16 所示, 使用递归算法可以很容易地进行计算.

• 图 6.16 计算所有链节的空间速度和加速度

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  function ForwardAllKinematics(j) global uLINK G if j == 0 return; end if j ~= 1 mom = uLINK(j).mother; %% Position and orientation uLINK(j).p = uLINK(mom).R * uLINK(j).b + uLINK(mom).p; uLINK(j).R = uLINK(mom).R * Rodrigues(uLINK(j).a, uLINK(j).q); %% Spatial velocity sw = uLINK(mom).R * uLINK(j).a; % axis vector in world frame sv = cross(uLINK(j).p, sw); % p_i x axis uLINK(j).w = uLINK(mom).w+ sw * uLINK(j).dq; uLINK(j).vo = uLINK(mom).vo + sv * uLINK(j).dq; %% Spatial acceleration dsv = cross(uLINK(mom).w, sv) + cross(uLINK(mom).vo, sw); dsw = cross(uLINK(mom).w, sw); uLINK(j).dw = uLINK(mom).dw+ dsw * uLINK(j).dq + sw * uLINK(j).ddq; uLINK(j).dvo = uLINK(mom).dvo + dsv * uLINK(j).dq + sv * uLINK(j).ddq; uLINK(j).sw = sw; % store h1 and h2 for future use uLINK(j).sv = sv; end ForwardAllKinematics(uLINK(j).sister); % Propagate to sister ForwardAllKinematics(uLINK(j).child); % Propagate to child

6.4.2 链节系统的反向动力学

接下来我们考虑作用在每个链节上的力和力矩. 为了做好准备, 让我们用空间速度向量 来重写 6.3 节中得到的刚体运动方程

$$\begin{bmatrix}\boldsymbol{f}\\ \boldsymbol{\tau}\end{bmatrix}=\boldsymbol{I}^S\dot{\boldsymbol{\xi}}+\boldsymbol{\xi}\times\boldsymbol{I}^S\boldsymbol{\xi}\tag{6.33}$$

其中运算符 表示以下计算.

$$\boldsymbol{\xi}\times=\begin{bmatrix} \boldsymbol{v}_{o}\\ \boldsymbol{\omega} \end{bmatrix}\times\equiv\begin{bmatrix} \hat{\boldsymbol{\omega}}&\boldsymbol{0}\\ \hat{\boldsymbol{v}}_o&\hat{\boldsymbol{\omega}} \end{bmatrix}.$$

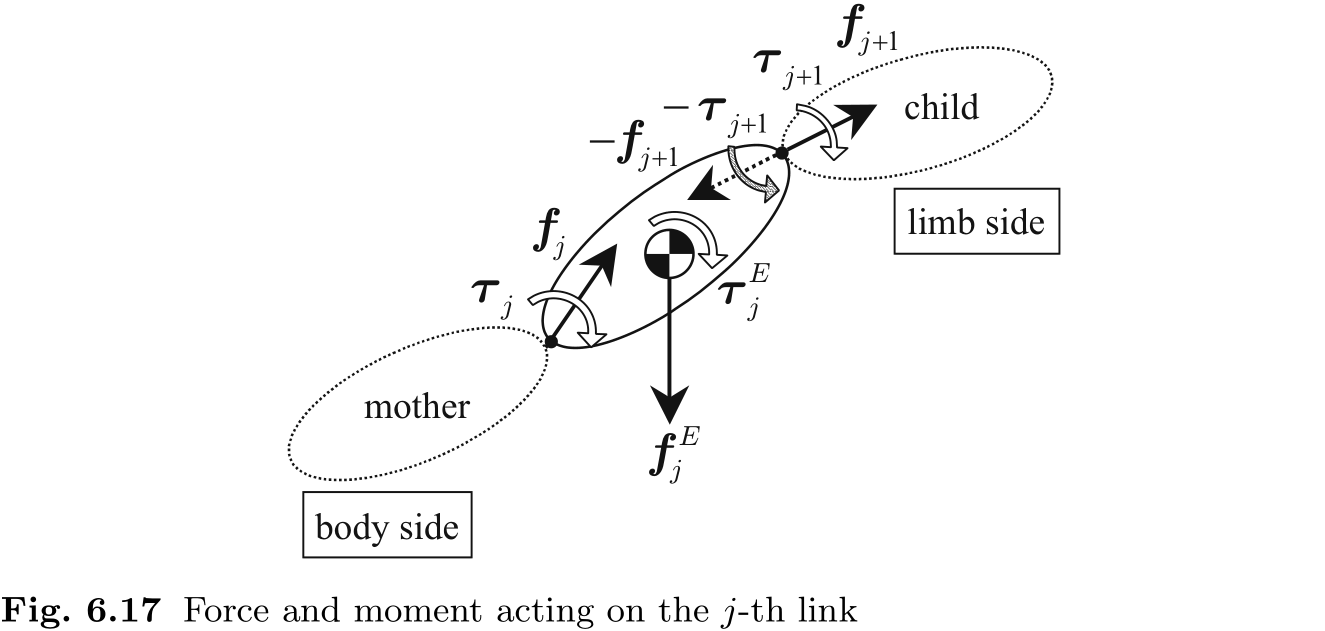
图 6.17 显示了作用在链节 上的力和力矩. 分别为从躯干一侧 (母链节) 到链节 的力和力矩.

环境直接作用在链节 上的力和力矩分别为 . 来自母链节, 环境和子链节反作用力的影响导致了链节 的运动. 运动方程为

$$\begin{bmatrix}\boldsymbol{f}_j\\ \boldsymbol{\tau}_j\end{bmatrix}+\begin{bmatrix}\boldsymbol{f}_j^E\\ \boldsymbol{\tau}_j^E\end{bmatrix}-\begin{bmatrix}\boldsymbol{f}_{j+1}\\ \boldsymbol{\tau}_{j+1}\end{bmatrix} =\boldsymbol{I}_j^S\dot{\boldsymbol{\xi}}_j+\boldsymbol{\xi}_j\times\boldsymbol{I}_j^S\boldsymbol{\xi}_j.\tag{6.35}$$

通过重写该方程, 我们可以得到一个递推方程, 给出力和力矩的传播情况

$$\begin{bmatrix}\boldsymbol{f}_j\\ \boldsymbol{\tau}_j\end{bmatrix} =\boldsymbol{I}_j^S\dot{\boldsymbol{\xi}}_j+\boldsymbol{\xi}_j\times\boldsymbol{I}_j^S\boldsymbol{\xi}_j-\begin{bmatrix}\boldsymbol{f}_j^E\\\boldsymbol{\tau}_j^E\end{bmatrix}+ \begin{bmatrix}\boldsymbol{f}_{j+1}\\ \boldsymbol{\tau}_{j+1}\end{bmatrix}.\tag{6.35}$$

当链节 为端点链节时, 变为零, 我们就可以计算出 . 因此, 当我们从端点链节开始计算时, 可以得到所有链节的力和力矩. 每个关节轴上的力矩 可计算为

$$u_j=\boldsymbol{s}_j^T\begin{bmatrix}\boldsymbol{f}_j\\ \boldsymbol{\tau}_j\end{bmatrix}.\tag{6.37}$$

通过图 6.18 中的递归算法实现了对这些方程的编程. 当链节系统有分支时, 该程序可以正常运行.

• 图 6.18 反向动力学代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  function [f,t] = InverseDynamics(j) global uLINK if j == 0 f = [0,0,0]'; t = [0,0,0]'; return; end c = uLINK(j).R * uLINK(j).c + uLINK(j).p; % Center of mass I = uLINK(j).R * uLINK(j).I * uLINK(j).R'; % Inertia tensor c_hat = hat(c); I = I + uLINK(j).m * c_hat * c_hat'; P = uLINK(j).m * (uLINK(j).vo + cross(uLINK(j).w,c)); % Momentum L = uLINK(j).m * cross(c,uLINK(j).vo) + I * uLINK(j).w; % Ang.momentum f0 = uLINK(j).m * (uLINK(j).dvo + cross(uLINK(j).dw,c)) + cross(uLINK(j).w,P); t0 = uLINK(j).m * cross(c,uLINK(j).dvo) + I * uLINK(j).dw + cross(uLINK(j).vo,P) + cross(uLINK(j).w,L); [f1,t1] = InverseDynamics(uLINK(j).child); % Force and moment form child f = f0 + f1; t = t0 + t1; if j ~= 1 uLINK(j).u = uLINK(j).sv' * f + uLINK(j).sw' * t; % Joint torque end [f2,t2] = InverseDynamics(uLINK(j).sister); % Force and moment from sister f = f + f2; t = t + t2;

本节所示的计算称为反向动力学. 通过前馈反动力学计算出的关节力矩, 我们可以实现快速, 精确的机器人运动. 这种控制技术称为计算力矩法. 不过, 要应用计算力矩法, 第一链节必须固定在地面上, 这样才能产生任意力和力矩. 工业机械臂的情况就是如此.

作为仿人机器人的基础链节, 机器人躯干并不是固定在地面上的, 因此无法保证机器人能够获得所需的力和力矩来保持所需的身体姿态. 如果运动模式不当, 机器人躯干的位置和朝向就会偏离预期. 这可以通过积分躯干加速度来仿真. 这是我们将在下一节讨论的正向动力学仿真的一种特殊变化. 在仿人机器人项目 (HRP) 开发的 OpenHRP 动态仿真器中, 这被称为高增益模式仿真 [31]. 在很多情况下, 这种仿真足以保证计划行走模式的稳定性.

6.4.3 链节系统的正向动力学

图 6.19 显示仿真结果, 其中 HRP-2 的所有关节力矩都设为零, 机器人瘫落到地面上.

仿真时, 机器人会受到来自环境的力和力矩以及自身关节力矩的作用, 从而完成各种运动. 计算机器人在给定关节力矩和外力作用下的运动称为正向动力学. 在本节中, 我们将根据前几节所学的知识, 解释正向动力学的基本计算方法.

一般来说, 由于躯干在三维空间中被视为自由链节, 因此具有 个关节的仿人机器人有 个自由度. 其运动方程的形式如下 [140, 77]

$$\boldsymbol{u}_G=\boldsymbol{A}_G\ddot{\boldsymbol{x}}_G+\boldsymbol{b}_G\tag{6.38}$$

其中, 是惯性矩阵, 是代表科里奥利力, 离心力和重力的向量. 是机器人的输入, 是加速度. 它们的定义是

$$\boldsymbol{u}_G\equiv\begin{bmatrix}\boldsymbol{f}_B\\ \boldsymbol{\tau}_B\\ \boldsymbol{u} \end{bmatrix},\quad \ddot{\boldsymbol{x}}_G\equiv\begin{bmatrix}\dot{\boldsymbol{v}}_{oB}\\ \dot{\boldsymbol{\omega}}_B\\ \ddot{\boldsymbol{q}} \end{bmatrix}$$

其中

: 物体上的力和力矩 (重力除外) ,

: 物体的空间加速度,

: 所有关节力矩 ,

: 所有关节加速度 .

如果已知 和 , 则给定输入 下的加速度计算公式为

$$\ddot{\boldsymbol{x}}_G=\boldsymbol{A}_G^{-1}(\boldsymbol{u}_G-\boldsymbol{b}_G).\tag{6.39}$$

这就是正向动力学的目标.

现在, 让我们定义一个函数 , 它可以根据上一节解释的反向动力学算法计算给定关节加速度下的关节力矩

$$\boldsymbol{u}_G=\text{InvDyn}(\ddot{\boldsymbol{x}}_G).\tag{6.40}$$

比较 (6.38) 和 (6.40) 可以发现, 可以通过 令加速度向量 计算

$$\boldsymbol{b}_G=\text{InvDyn}(\boldsymbol{0}).\tag{6.41}$$

接下来, 我们假设有一个 向量 , 其第 个元素为 1, 其他元素均为 0. 通过设置 , 我们得到

$$\boldsymbol{A}_G\boldsymbol{\delta}_i=\text{InvDyn}(\boldsymbol{\delta}_i)-\boldsymbol{b}_G.\tag{6.42}$$

上式左侧表示矩阵 的第 行. 因此, 如果我们重复计算, 将 从 1 遍历到 , 就可以得到 的所有分量. 这种方法称为单位向量法, 由 Walker 和 Orin [92] 提出.

得到 和 后, 就可以直接使用 (6.39) 计算加速度了. 通过积分, 我们可以对机器人进行动力学仿真.

图 6.20 给出了一段 Matlab 代码, 该代码基于单位向量法计算物体的空间加速度和关节加速度. 计算 的程序见本章末附录中的图 6.29.

• 图 6.20 基于单位向量法的正向动力学

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  nDoF = length(uLINK)-1+6; A = zeros(nDoF,nDoF); b = InvDyn(0); for n = 1:nDoF A(:,n) = InvDyn(n) - b; end % add motor inertia for n = 7:nDoF j = n-6+1; A(n,n) = A(n,n) + uLINK(j).Ir * uLINK(j).gr^2; end u = [0 0 0 0 0 0 u_joint(2:end)']'; ddq = A(-b + u); uLINK(1).dvo = ddq(1:3); uLINK(1).dw = ddq(4:6); for j = 1:length(uLINK)-1 uLINK(j+1).ddq = ddq(j+6); end

虽然单位向量法易于理解和编程, 但当机器人关节数量增加时, 其性能会迅速下降. 第一个问题是惯性矩阵的计算方法. 对于有 个关节的机器人, 单位向量法要进行 次反向动力学计算, 才能得到 . 由于一次逆动力学计算的时间与 成正比, 因此总计算时间的增加与 成正比. 这个问题可以通过引入一种直接计算惯性矩阵的算法来解决 [92, 30].

第二个也是更本质的问题是求解 (6.39), 这是一个庞大的线性方程组. 虽然已知有 Gauss-Jordan 消元或 LU 分解等高效算法 [136], 但其耗时总是与 成正比, 成为快速正向动力学计算的严重瓶颈. 下一节, 我们将介绍解决这一问题的方法.

6.4.4 Featherstone 方法

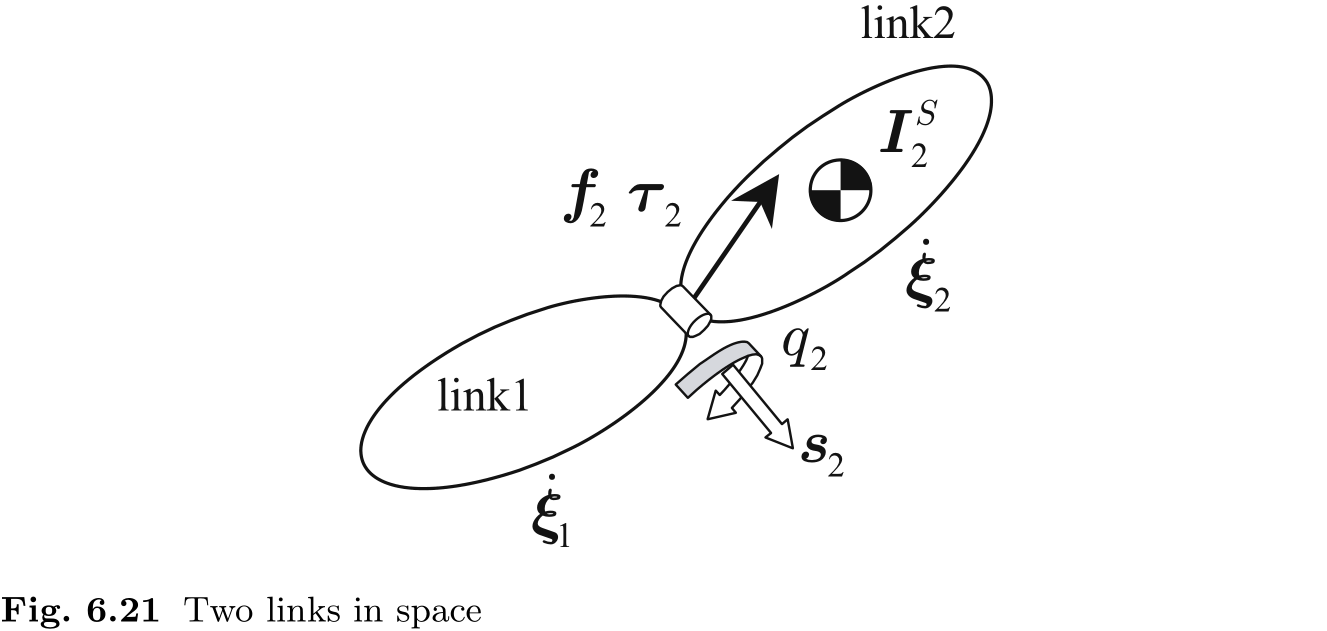
假设如图 6.21 所示, 有两个链节通过一个漂浮在三维空间中的旋转接头相连. 假定我们已经知道链节 1 的空间加速度, 我们希望推导出给定力矩 时的关节加速度 . 链节 2 的空间加速度由以下公式给出

$$\dot{\boldsymbol{\xi}}_2=\dot{\boldsymbol{\xi}}_1+\dot{\boldsymbol{s}}_2\dot{q}_2+\boldsymbol{s}_2\ddot{q}_2.\tag{6.43}$$

根据加速度, 我们可以利用运动方程计算出必要的力和力矩.

$$\begin{bmatrix}\boldsymbol{f}_2\\ \boldsymbol{\tau}_2\end{bmatrix}=\boldsymbol{I}_2^S\dot{\boldsymbol{\xi}}_2+\boldsymbol{\xi}_2\times\boldsymbol{I}_2^S\boldsymbol{\xi}_2.\tag{6.44}$$

此外, 关节力矩 是该力和力矩的投影

$$u_2=\boldsymbol{s}_2^T\begin{bmatrix}\boldsymbol{f}_2\\ \boldsymbol{\tau}_2\end{bmatrix}.\tag{6.45}$$

将 (6.43) 和 (6.44) 代入该方程, 我们就可以求解出关节加速度了

$$\ddot{q}_2=\frac{u_2-\boldsymbol{s}_2^T(\boldsymbol{I}_2^S(\dot{\boldsymbol{\xi}}_1+\dot{\boldsymbol{s}}_2\dot{q}_2)+\boldsymbol{\xi}_2\times\boldsymbol{I}_2^S\boldsymbol{\xi}_2)}{\boldsymbol{s}_2^T\boldsymbol{I}_2^S\boldsymbol{s}_2}.\tag{6.46}$$

根据这一方程, 我们可以立即计算出给定关节力矩 的关节加速度 , 而无需处理上一节 (6.39) 中出现的惯性矩阵.

但是, 只有当链节 2 是最外层链节时, 我们才能使用 (6.46). 如果从链节 2 开始有额外的链节, 如图 6.22 所示, (6.44) 将不再有效.

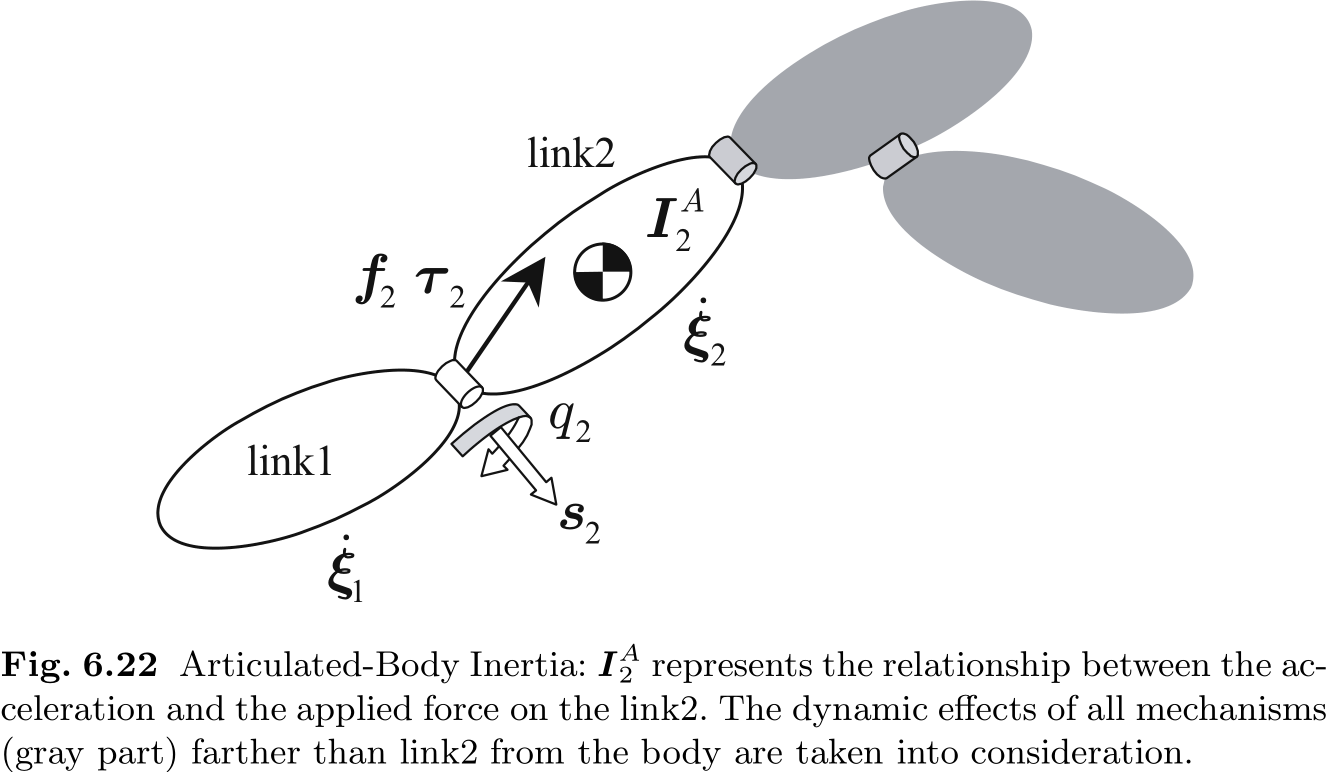
使用 (6.46) 的一种方法是引入一个新的惯性张量 , 它包含比链节 2 更远的额外链节的所有影响, 它满足

$$\begin{bmatrix}\boldsymbol{f}_2\\ \boldsymbol{\tau}_2\end{bmatrix}=\boldsymbol{I}_2^A\dot{\boldsymbol{\xi}}_2+\boldsymbol{b}_2.\tag{6.47}$$

称为铰接体惯性 (articulated-body inertia). 铰接体惯性矩阵表示加速度与作用在相关链节上的力之间的关系. 是偏置力, 包括科里奥利力, 离心力和重力以及作用在比链节 2 更远的结构上的关节力矩.

Featherstone 指出, 铰接体的惯性可以通过递推方程计算得出

$$\boldsymbol{I}_{j}^{A}=\boldsymbol{I}_{j}^{S}+\boldsymbol{I}_{j+1}^{A}-\frac{\boldsymbol{I}_{j+1}^{A}\boldsymbol{s}_{j+1}\boldsymbol{s}_{j+1}^T\boldsymbol{I}_{j+1}^{A}}{\boldsymbol{s}_{j+1}^T\boldsymbol{I}_{j+1}^{A}\boldsymbol{s}_{j+1}}.\tag{6.48}$$

偏置力也可以用类似的公式计算.

假设我们已经计算了铰接体惯性和所有链节的偏置力. 将 (6.47) 和 (6.43) 代入 (6.45), 我们得到

$$\ddot{q}_2=\frac{u_2-\boldsymbol{s}_2^T(\boldsymbol{I}_2^A(\dot{\boldsymbol{\xi}}_1+\dot{\boldsymbol{s}}_2\dot{q}_2)+\boldsymbol{b}_2)}{\boldsymbol{s}_2^T\boldsymbol{I}_2^S\boldsymbol{s}_2}.\tag{6.49}$$

即用给定的关节力矩直接计算关节加速度的方程. 这就是 Featherstone 理论的核心.

总之, 正向动力学的计算可通过以下三个步骤进行.

1. 计算从主体链节到外部链节的所有链节的位置, 朝向和空间速度 (正向运动学) .
2. 计算铰接体惯性和从最外侧链节到主体链节的所有链节的偏置力.
3. 根据 (6.49) 计算关节加速度, 根据 (6.43) 计算从躯干链节到外部链节的链节空间加速度.

由于每一步所需的时间与关节数 成正比, 因此总计算时间也与 成正比. 这种算法被称为具有 阶速度, 或表示为 . 例如, 上一节中的单位向量法就是 , 因为它所需的时间与 的立方成正比. 我们在 Matlab 上实现了 Featherstone 算法. 对于 HRP-2 , 它比单位向量法快约 20 倍.

6.5 本节的背景材料

17 至 18 世纪, 牛顿, 欧拉和其他科学家建立了物体运动的基本理论. 然而, 这并不是研究的终点.

事实上, 大约二十年前, 一位本科生试图仿真一个具有十二自由度的双足机器人, 于是他开始手工计算运动方程. 他花了整整一个暑假的时间, 用了整整一个笔记本来记下计算出的方程. 当时, 有一些商业仿真软件可以处理复杂的机械系统, 但这些软件非常昂贵, 而且专门用于称为工程工作站的计算机, 其价格令人望而却步. 此外, 即使使用这样的软件, 仿真一个简单的双足机器人走几步路也需要几个小时！

本章介绍的高效, 优雅的动态计算方法极大地改变了这种状况. 这些算法是由机器人和航空工程研究人员在 20 世纪 80 年代和 90 年代开发的. 目前, 最先进的技术可以实现实时动力学仿真. 此外, 研究人员仍在努力改进, 他们最近提出了基于并行计算的 算法 [98, 78]. 这些快速动力学仿真的应用不仅限于机器人技术, 还可用于分析太阳能电池板膨胀时的卫星运动, 或在电影和交互式计算机游戏中通过计算机图形将逼真的场景可视化.

6.6 附录

6.6.1 力和力矩的处理

在本节中, 所有运动方程都在世界坐标系中表示, 因此力和力矩必须相对于世界坐标系来书写. 例如, 即使是作用在物体运动中心点上的重力, 我们也必须考虑它绕世界坐标系原点的力矩. 虽然这看起来很复杂, 但我们可以正确计算多刚体之间的相互作用.

将力和力矩转换到世界坐标系的基本规则如下.

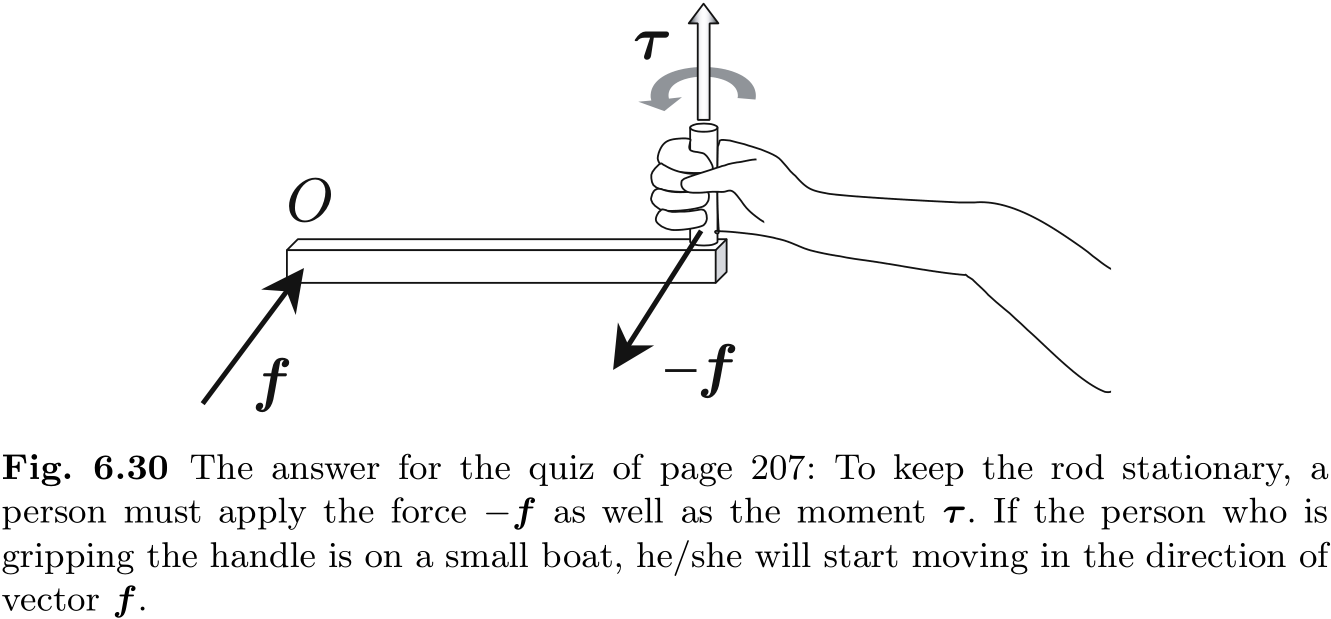
• 规则 1: 作用在点 上的力 相对于世界坐标系转换为力 和力矩 (图 6.23(a)) .
• 规则 2: 作用在点 上的力矩 与相对于世界坐标系的 是相同的 (图 6.23(b)) .

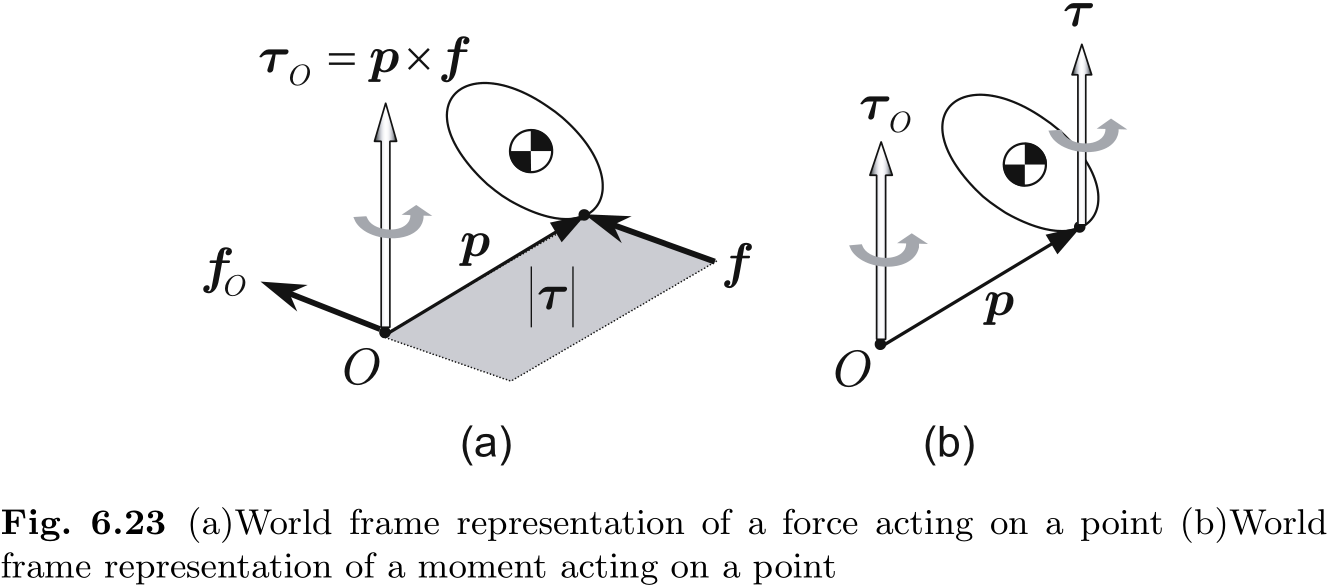
一般来说, 当力 和力矩 同时作用在点 上时, 它们会转换成绕原点的力和力矩 , 其公式为

$$\begin{bmatrix}\boldsymbol{f}_o\\ \boldsymbol{\tau}_o\end{bmatrix}=\begin{bmatrix}\boldsymbol{f}_p\\ \boldsymbol{p}\times\boldsymbol{f}_p+\boldsymbol{\tau}_p\end{bmatrix}.\tag{6.50}$$

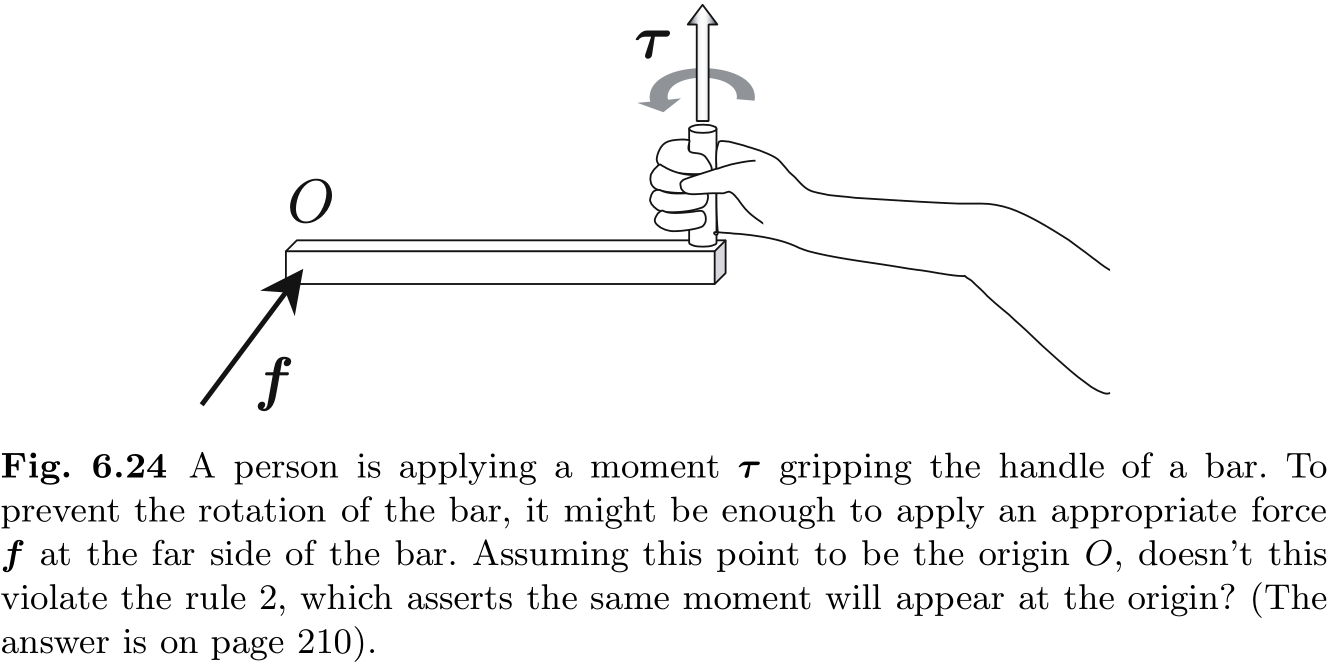
我们可能会认为它们是显而易见的, 但我们往往会在这类计算中犯一个奇怪的错误. 图 6.24 所示的测验可能有助于理解这个问题.

6.6.2 子程序

• 图 6.25 ShowObject.m: 显示对象的动画

  1 2 3 4 5 6 7 8 9

  vert = uLINK(1).R * uLINK(1).vertex; % rotation for k = 1:3 vert(k,:) = vert(k,:) + uLINK(1).p(k); % translation end newplot h = patch('faces',uLINK(1).face','vertices',vert','FaceColor',[0.5 0.5 0.5]); axis equal; view(3); grid on; xlim(AX); ylim(AY); zlim(AZ); text(0.25, -0.25, 0.8, ['time=',num2str(time(n),'%5.3f')]) drawnow

• 图 6.26 MakeRigidBody.m: 设置刚体及其参数

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  function MakeRigidBody(j, wdh, mass) global uLINK uLINK(j).m = mass; % mass uLINK(j).c = [0 0 0]'; % center of mass uLINK(j).I = [ 1/12*(wdh(2)^2 + wdh(3)^2) 0 0; 0 1/12*(wdh(1)^2 + wdh(3)^2)0; 0 0 1/12*(wdh(1)^2 + wdh(2)^2)] * uLINK.m; % inertia tensor uLINK(j).vertex = 0.5*[ -wdh(1) -wdh(2) -wdh(3); -wdh(1) wdh(2) -wdh(3); wdh(1) wdh(2) -wdh(3); wdh(1) -wdh(2) -wdh(3); -wdh(1) -wdh(2) wdh(3); -wdh(1) wdh(2) wdh(3); wdh(1) wdh(2) wdh(3); wdh(1) -wdh(2) wdh(3); ]'; % vertex points uLINK(1).face = [ 1 2 3 4; 2 6 7 3; 4 3 7 8; 1 5 8 4; 1 2 6 5; 5 6 7 8; ]'; % polygons

• 图 6.27 MakeTop.m: 设置陀螺及其参数

  1 2 3 4 5 6 7 8 9 10 11 12 13

  function MakeTop(j, r,a,c) global uLINK [vertex1,face1] = MakeZcylinder([0 0 c]',r,a); % shape of disk [vertex2,face2] = MakeZcylinder([0 0 c]',0.01,2*c); % shape of shaft uLINK(j).vertex = [vertex1 vertex2]; face2 = face2 + size(vertex1,2); uLINK(j).face = [face1 face2]; density = 2.7E+3; % density of aluminum [kg/m^2] uLINK(j).m = pi*r^2*a*density; % mass of the disk [kg] uLINK(j).I = [ (a^2 + 3*r^2)/12 0 0; 0 (a^2 + 3*r^2)/120; 0 0 r^2/2] * uLINK.m; % inertia tensor of the disk uLINK(j).c = [0 0 c]'; % center of mass

• 图 6.28 MakeZcylinder.m: 创建圆柱体形状

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  function [vert,face] = MakeZcylinder(pos, radius,len) a = 10; % regular polygon for circle theta = (0:a-1)/a * 2*pi; x = radius*cos(theta); y = radius*sin(theta); z1 = len/2 * ones(1,a); z2 = -z1; vert= [x x 0 0; y y 0 0; z1 z2 len/2 -len/2]; % vertices for n = 1:3 vert(n,:) = vert(n,:) + pos(n); end face_side = [1:a; a+1:2*a; a+2:2*a a+1; 2:a 1]; face_up = [1:a; 2:a 1]; face_up(3:4,:) = 2*a+1; % index of up center face_down = [a+2:2*a a+1; a+1:2*a]; face_down(3:4,:) = 2*a+2; % index of down center face = [face_side face_up face_down];

• 图 6.29 InvDyn.m: 用单位向量法进行反向动力学计算

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  function ret = InvDyn(j) global uLINK uLINK(1).dvo = [0 0 0]'; uLINK(1).dw = [0 0 0]'; if j >= 1 & j <= 3 uLINK(1).dvo(j) = 1; elseif j >= 4 & j <= 6 uLINK(1).dw(j-3) = 1; end for n = 1:length(uLINK)-1 if n == j-6 uLINK(n+1).ddq = 1; else uLINK(n+1).ddq = 0; end end ForwardAllKinematics(1); [f,tau] = InverseDynamics(1); ret = [f',tau',uLINK(2:end).u]';