本文为书籍 Introduction to Humanoid Robotics 的汉化, 主要借助翻译器 DeepL.

另外, 原书有管贻生教授的译作版本:《仿人机器人》(清华大学出版社, 2007年). 强烈推荐.

---

4 双足行走 (Biped Walking)

"Walk" 一词的意思是什么? 牛津高阶词典给出了简明的定义.

walk:
move along at a moderate pace by lifting up and putting down each foot in turn, so that one foot is on the ground while the other is being lifted (Oxford Advanced Learner's Dictionary, Oxford University Press)

因此, 在行走过程中, 任何时刻都必须至少有一只脚与地面接触. 行走分为两种, 即静态行走和动态行走. 在 "静态行走" 中, 质心的投影在行走过程中从未离开过支撑多边形. 在 "动态行走" 中, 质心的投影会有一段时间离开支撑多边形.

$$\text{行走}\left\{ \begin{array}{l} 静态行走\\ 动态行走 \end{array} \right.$$

大多数玩具机器人使用大脚进行静态行走. 从控制工程的角度来看, 这并不有趣, 因为它相当容易. 然而, 人类的脚相对于质心高度来说太小, 无法进行静态行走. 事实上, 我们在日常生活中都在进行动态行走. 我们习以为常的行走方式可以通过灵巧地控制本质上不稳定的全身平衡来实现. 因此, 双足行走机械超出了传统机械工程的范畴. 正因为如此, 许多研究人员和工程师对双足行走机械和仿人机器人情有独钟.

4.1 如何实现双足行走?

图 4.1 显示了本章将使用的双足行走控制基本框架. 我们使用行走模式生成器来创建行走模式. 在理想情况下, 只需给实际机器人一个行走模式, 就能实现双足行走 (图 4.1(a)) . 为此, 我们必须准备一个精确的机器人模型, 一个能完全按照指令运动的刚性机械和一个完美的水平地面 (一个巨大的表面板) .

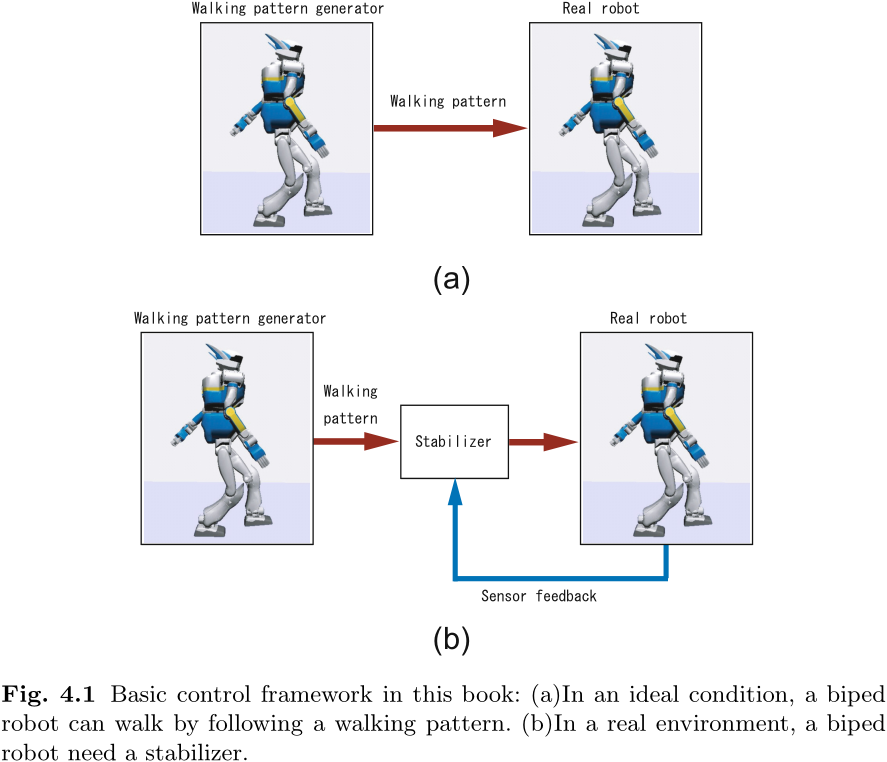
另一方面, 在实际情况中, 一个真人大小的仿人机器人很容易因为地面几毫米的不平整而摔倒. 人形机器人的比例和质量分布往往会迅速放大姿态误差, 使其达到不稳定的程度. 为了抑制这种情况, 我们需要第二个软件, 利用陀螺仪, 加速度计, 力传感器和其他装置来修改行走模式. 这就是所谓的稳定器 (图 4.1(b)) .

本章接下来的内容安排如下. 在第 4.2, 4.3 和 4.4 节中, 我们解释了行走模式生成器, 并在第 4.5 节中解释了稳定器. 在第 4.6 节中, 我们简要介绍了双足行走机器人的研究历史. 在第 4.7 节中, 我们将介绍不受图 4.1 框架限制的各种双足控制方法.

4.2 二维行走模式生成

在本节中, 我们将考虑二维双足行走的基本原理, 并推导出一种行走模式生成算法.

4.2.1 二维倒立摆

近似化是处理复杂系统的有力方法. 在天体力学中, 研究人员将太阳和行星近似为质点, 而它们有自己的内部结构, 他们仍然可以足够精确地计算太阳系的轨道. 在热力学中, 庞大的分子状态 (数量级为 ) 被近似化为温度或熵等几个参数, 这使我们有可能预测热力学现象.

同样, 为了提取双足运动的本质, 我们在对一个由数千个机械和电气部件组成, 具有 30 多个 DOF 的仿人机器人进行近似化训练时做了三个假设. 首先, 我们假设机器人的所有质量都集中在其质心 (CoM) 处. 其次, 我们假设机器人的腿是无质量的, 其顶端通过单个旋转关节与地面接触. 最后, 我们只考虑机器人的前后和上下运动, 忽略横向运动. 换句话说, 我们假设机器人的运动受限于由行走方向轴和垂直轴定义的矢状面. 根据这些假设, 我们将机器人建模为二维倒立摆, 如图 4.2 所示.

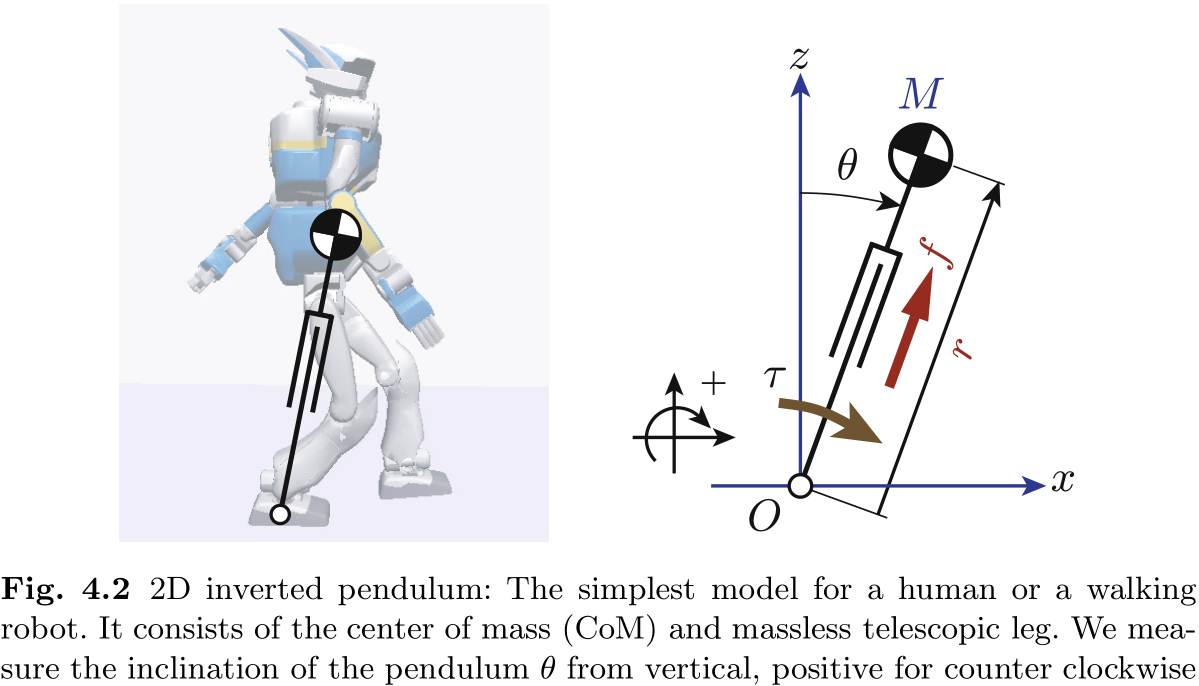
倒立摆的输入是支点处的力矩 和沿腿棱柱关节处的踢力 . 倒立摆的动力学由以下几个微分方程描述

$$r^2\ddot{\theta}+2r\dot{r}\dot{\theta}-gr\sin\theta=\tau/M\\ \ddot{r}-r\dot{\theta}^2+g\cos\theta=f/M.$$

这些方程可以通过拉格朗日方法推导出来. 约瑟夫-路易-拉格朗日 (1736-1813 年) 是出生在意大利的法国数学家. 他是著名的拉格朗日点发现者, 拉格朗日点是最适合放置太空殖民地的区域.

我们可以在给定输入力矩的情况下, 通过对它们进行数值积分来模拟倒立摆的行为.

其中一个重要的限制是, 由于双足机器人的脚非常小, 我们不能使用大的力矩 . 如果行走机器人像高跷一样有点接触, 我们就必须使用

$$\tau=0.\tag{4.1}$$

在这种情况下, 摆几乎总是向下倒, 除非中心点正好位于支点上方. 如图 4.3 所示, 即使是这样一个简单的摆, 我们也可以根据不同的踢力 来选择不同的下落方式.

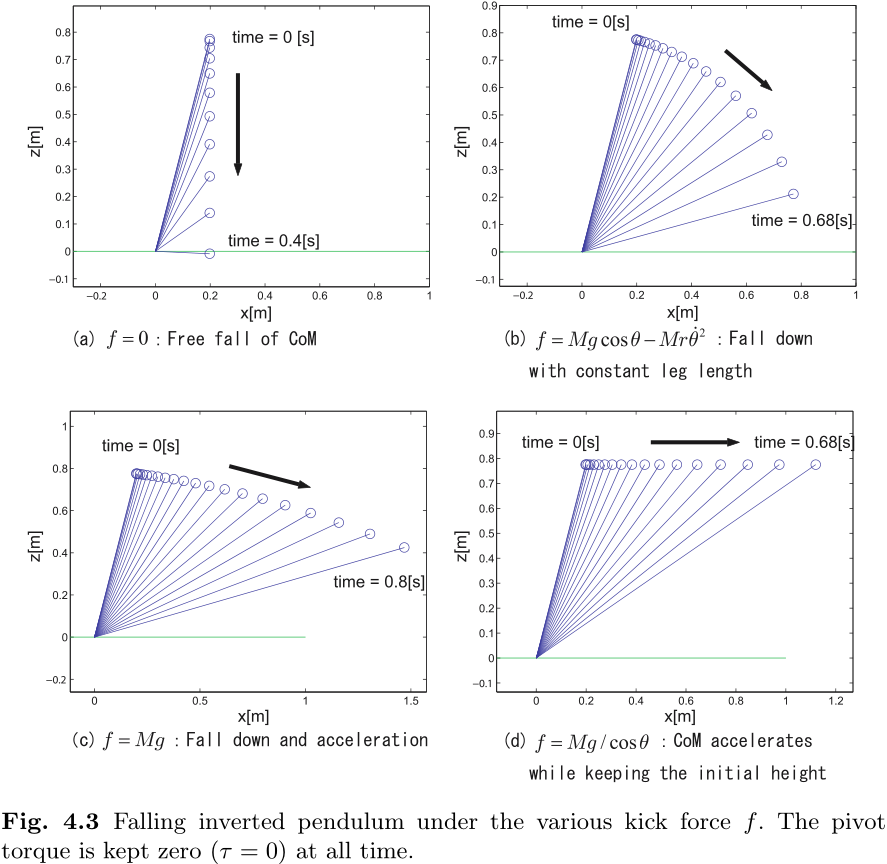
最有趣的情况是图 4.3(d), CoM 在踢力作用下水平移动

$$f=\frac{Mg}{\cos\theta}.\tag{4.2}$$

图 4.4 说明了 CoM 呈现水平运动的原因.

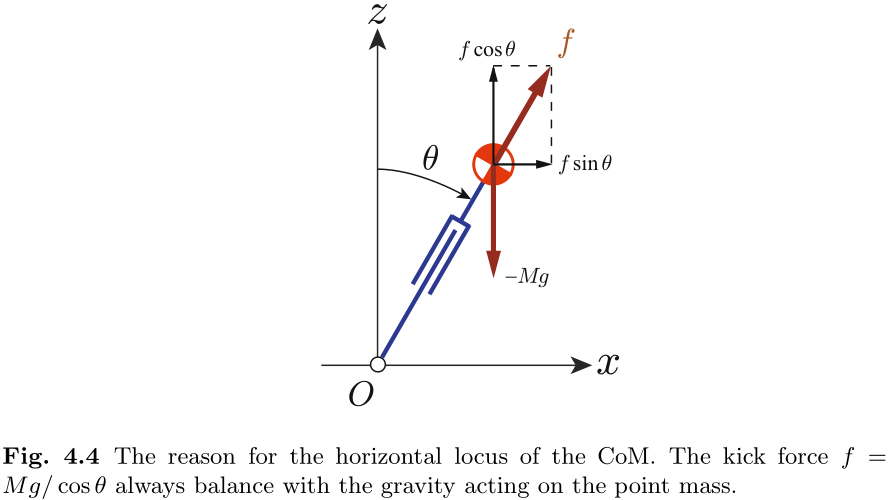
直观地说, 我们可以说, 摆在下落的过程中通过快速伸出摆腿来保持 CoM 高度. 我们称之为线性倒立摆 (Linear Inverted Pendulum) [115].

这是线性倒立摆 (LIP) 的最简单版本. 本章将对这一概念进行延伸. 此外, 线性倒立摆也是零动力学的一个例子, Westervelt 等人的教科书[24]对零动力学进行了讨论.

4.2.2 线性倒立摆的行为

线性倒立摆为我们提供了一种简单的动力学数学处理方法. 让我们研究一下水平运动.

① 水平动力学

通过再次研究图 4.4, 我们可以看到踢力 的水平分量仍然存在, 而垂直分量则被重力抵消. 水平分量会水平加速 CoM, 因此我们可以得出

$$M\ddot{x}=f\sin\theta.\tag{4.3}$$

将 (4.2) 代入, 可得

$$M\ddot{x}=\frac{Mg}{\cos\theta}\sin\theta=Mg\tan\theta=Mg\frac{x}{z},$$

其中, , 给出了倒立摆的 CoM. 通过对上式的重写, 我们可以得到一个关于 CoM 水平动力学的微分方程

$$\ddot{x}=\frac{g}{z}x.\tag{4.4}$$

由于线性倒立摆的 值恒定, 我们可以轻松求解这个常微分方程

$$x(t)=x(0)\cosh(t/T_c)+T_c\dot{x}(0)\sinh(t/T_c)\tag{4.5}$$ $$\dot{x}(t)=x(0)/T_c\sinh(t/T_c)+\dot{x}(0)\cosh(t/T_c)\tag{4.6}$$ $$T_c\equiv\sqrt{z/g}$$

其中, 是时间常数, 取决于 CoM 的高度和重力加速度.

初始位置和速度分别为 , , 它们合称为初始条件. 图 4.5 显示了不同初始条件下的运动.

② 转移时间

在许多情况下, 我们想知道 CoM 从一点到另一点所需的时间. 当给出某一时刻的初始条件 和条件 时, 利用 (4.5) 和 (4.6) 将它们用以下方程连接起来

$$x_1=x_0\cosh(\tau/T_c)+T_c\dot{x}_0\sinh(\tau/T_c)\tag{4.7}$$ $$\dot{x}_1=x_0/T_c\sinh(\tau/T_c)+\dot{x}_0\cosh(\tau/T_c)\tag{4.8}$$

其中, 是 CoM 从 到 的周期.

利用 , 的关系, 这些方程可以改写为

$$x_1=\frac{x_0+T_c\dot{x}_0}{2}e^{\tau/T_c}+\frac{x_0-T_c\dot{x}_0}{2}e^{-\tau/T_c},\tag{4.9}$$ $$\dot{x}_1=\frac{x_0+T_c\dot{x}_0}{2T_c}e^{\tau/T_c}-\frac{x_0-T_c\dot{x}_0}{2T_c}e^{-\tau/T_c}.\tag{4.10}$$

由 可得

$$x_1+T_c\dot{x}_1=(x_0+T_c\dot{x}_0)e^{\tau/T_c}.$$

因此, 的计算公式为

$$\tau=T_c\ln\frac{x_1+T_c\dot{x}_1}{x_0+T_c\dot{x}_0}.\tag{4.11}$$

同样, 我们可以根据 计算出 为

$$\tau=T_c\ln\frac{x_0-T_c\dot{x}_0}{x_1-T_c\dot{x}_1}.\tag{4.12}$$

基本上, (4.11) 和 (4.12) 得到的结果完全相同, 只是在奇异的情况下, 其中一个方程的分子和分母都趋近于零.

4.2.3 轨道能量

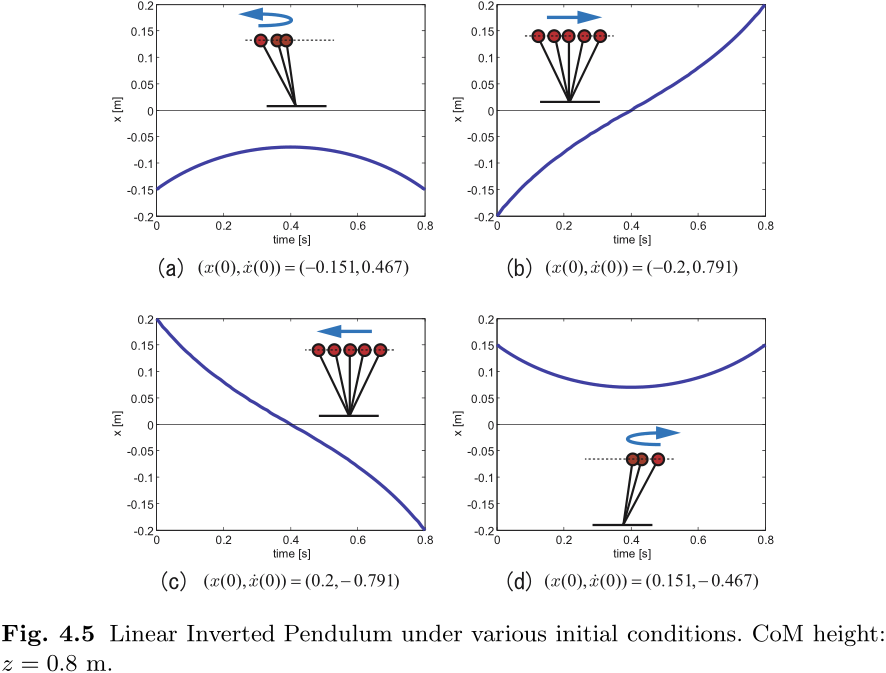
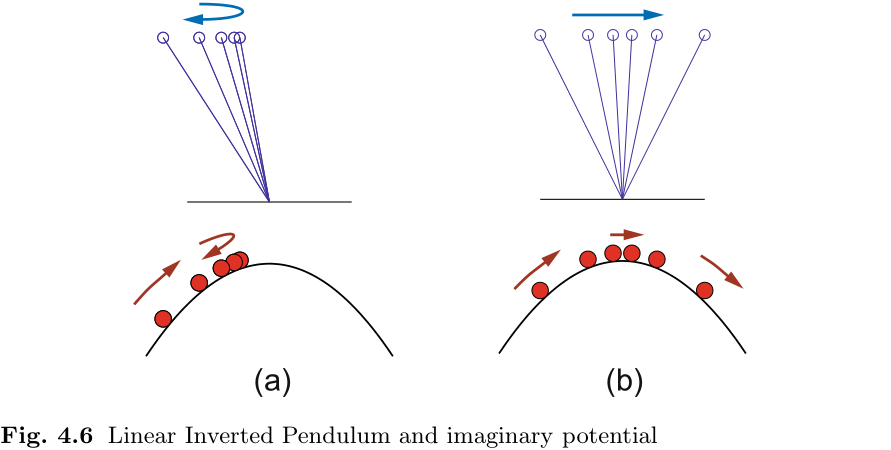
为了直观地理解线性倒立摆的运动, 不妨想象一下图 4.6 所示的势能. 图 4.6(a) 显示了当初始速度不足时 CoM 改变运动方向的情况. 在图 4.6(b) 中, 由于初始速度足够大, CoM 保持原来的运动方向. 在这种情况下, CoM 在势能顶端的速度最小, 此时 CoM 位于踝支点上方.

让我们来计算一下这个虚势与 CoM 运动之间的关系. 我们将 乘以运动方程 (4.4) 的两边, 然后进行积分

$$\begin{align*} \dot{x}\left(\ddot{x}-\frac{g}{z}x\right)&=0\\ \int\left(\ddot{x}\dot{x}-\frac{g}{z}x\dot{x}\right)dt&=\text{constant}. \end{align*}$$

结果如下

$$\frac{1}{2}\dot{x}^2-\frac{g}{2z}x^2=\text{constant}\equiv E.\tag{4.13}$$

左侧第一项是动能, 第二项是虚势能, 如图 4.6 所示. 在计算中, 我们假设单位质量的能量, 这样就可以省略 CoM 的质量.

我们把动能和虚势能之和称为 , 即轨道能量[36]. 方程 (4.13) 表明, 在线性倒立摆的运动中, 轨道能量是守恒的.

在力学中, 这个值被称为运动常数 [36].

在图 4.6(a) 中, CoM 没有到达势能的顶端就发生了回转, 轨道能量为

$$E=-\frac{g}{2z}x^2_{rev},\tag{4.14}$$

其中 是回归时刻 CoM 的水平位置. 在这种情况下, 轨道能量为负或零.

在图 4.6(b) 中, 当 CoM 穿过势顶时, 轨道能量为

$$E=\frac{1}{2}\dot{x}_{top}^2,\tag{4.15}$$

其中, 是 CoM 经过踝支点上方时的速度. 在这种情况下, 轨道能量为正.

假设我们已经得到了倒立摆在某一时刻的 CoM 位置和速度. 通过检查 (4.13) 计算出的轨道能量 的符号, 我们可以立即预测 CoM 是否会通过势能顶端. 如果 E > 0, 我们可以预测 CoM 在势能顶端的速度为

$$|\dot{x}_{top}|=\sqrt{2E}.$$

如果 , 我们可以预测 CoM 回归的位置为

$$|x_{rev}|=\sqrt{-\frac{2zE}{g}}.$$

4.2.4 支撑腿交换

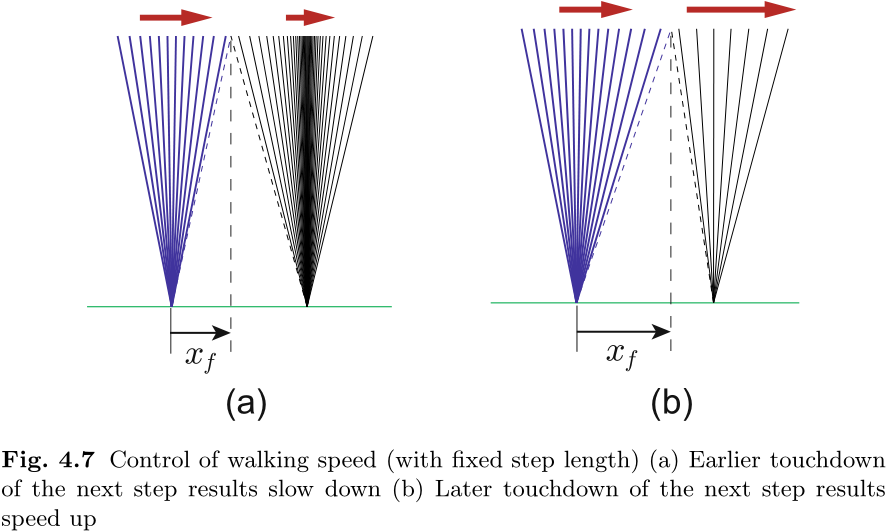
虽然线性倒立摆的运动仅由其初始条件决定, 但我们可以控制其速度, 因为初始条件可以通过触地时间来改变. 如图 4.7 所示, 加速触地的支撑腿交换会降低行走速度, 而延迟触地的支撑交换会加快行走速度. 这与我们的经验相符, 例如, 我们在急刹车时会迅速将腿放在地上.

让我们来弄清楚支撑腿交换和倒立摆运动之间的关系. 图 4.8 显示了支撑腿交换的力矩. 步长为 , CoM 相对于前接触点的位置为 , CoM 在交换瞬间的速度为 . 为简单起见, 我们假设腿部支撑瞬间交换, 因此 既是前一个支撑阶段的最终速度, 也是新支撑阶段的初始速度.

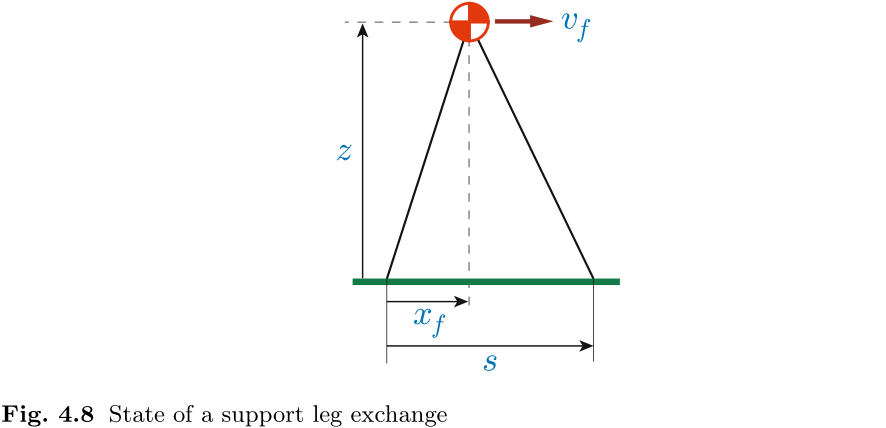
通过将交换前后的轨道能量分别定义为 和 , 我们得出

$$E_1=-\frac{g}{2z}x_f^2+\frac{1}{2}v_f^2,\tag{4.16}$$ $$E_2=-\frac{g}{2z}(x_f-s)^2+\frac{1}{2}v_f^2.\tag{4.17}$$

当给出轨道能量 和 时, 我们可以通过从 (4.16) 和 (4.17) 中消去 来计算必要的交换条件, 从而得到

$$x_f=\frac{z}{gs}(E_2-E_1)+\frac{s}{2}.\tag{4.18}$$

交换瞬间的速度可根据 (4.16) 计算得出

$$v_f=\sqrt{2E_1+\frac{g}{z}x_f^2}.\tag{4.19}$$

4.2.5 规划简单的双足步态

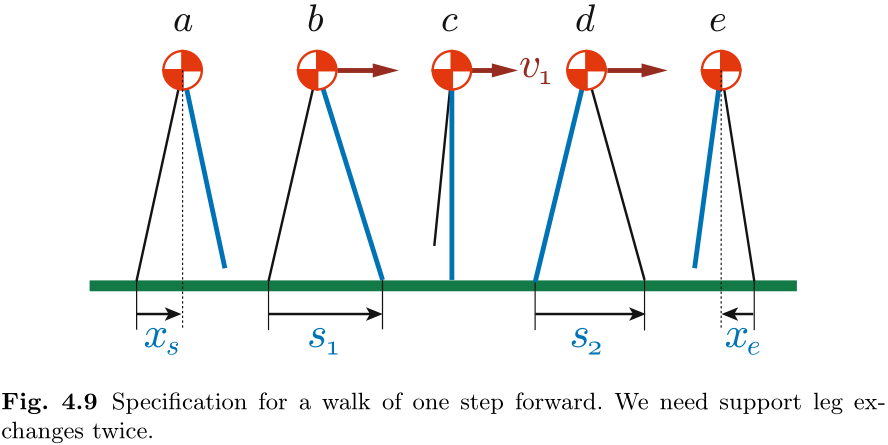
让我们利用前几节的结果设计一个简单的行走模式. 我们假设一个理想的双足机器人在水平面上只走一步就停下来 (图 4.9) . 机器人要交换两次支撑, 必须指定三个轨道能量. 对于开始行走 (ab) , 轨道能量由 CoM 的初始位置指定,

$$E_0=-\frac{g}{2z}x_s^2.$$

对于步骤 (bcd) , 轨道能量由 CoM 经过支撑点时的速度 确定

$$E_1=\frac{1}{2}v_1^2.$$

对于行走终点 (de) , 轨道能量由 CoM 的最终位置确定.

$$E_2=-\frac{g}{2z}x_e^2.$$

利用 (4.18), 可以从 , 得到第一个支撑交换条件 , 从 , 得到第二个支撑交换条件 . 通过控制摆动腿, 使这些交换在正确的时间发生, 就能实现预期的行走运动.

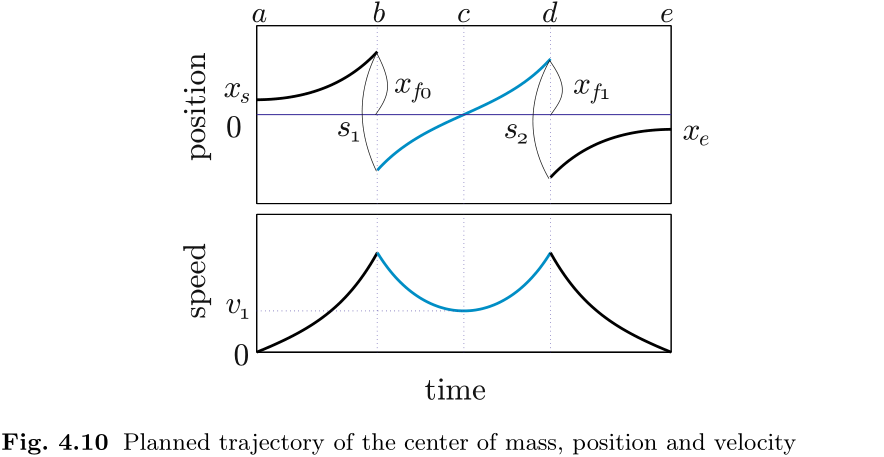
由于每次交换时的速度都由 (4.19) 计算得出, 因此可以得到每一步的完整轨迹. 图 4.10 显示了 CoM 位置和速度的时间曲线. 位置图以每个支撑点为原点, 因此在交换支撑点 的时刻, 位置图会发生跳变, 跳变量表示步长. 速度曲线图描绘了 CoM 速度的动态变化和支撑物交换时的峰值.

4.2.6 拓展至在不平坦的地形上行走

虽然前面介绍的方法仅限于在平地上行走, 但只要稍加改动, 我们也可以用同样的方法在不平坦的地形上行走. 让我们来解释一下.

回到图 4.2 的倒立摆模型, 我们考虑质心在斜线上移动的情况, 如图 4.11 所示, 描述如下

$$z=kx+z_c\tag{4.20}$$

其中, 为直线的倾角, 为直线的 轴交点. 我们将 CoM 沿其移动的直线称为约束线.

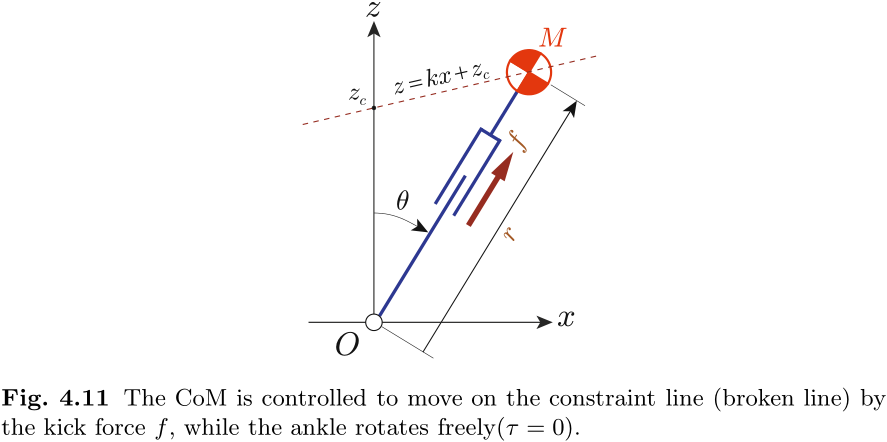
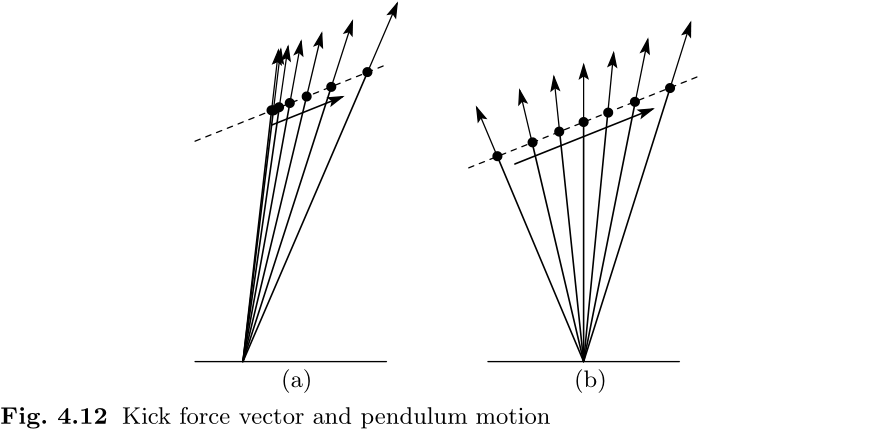
让我们计算一下实现这种运动的踢力 . 首先, 我们将踢力 分解为水平部分 和垂直部分

$$f_x=f\sin\theta=(x/r)f,\tag{4.21}$$ $$f_z=f\cos\theta=(z/r)f.\tag{4.22}$$

要让 CoM 沿约束线移动, 踢力和重力之和必须与约束线平行. 解释如下

$$f_x:f_z-Mg=1:k.\tag{4.23}$$

将 (4.21) 和 (4.22) 代入 (4.23) 并求解 , 可得

$$f=\frac{Mgr}{z-kx}.\tag{4.24}$$

利用约束方程 (4.20) 可以得到一个更简单的方程

$$f=\frac{Mgr}{z_c}.\tag{4.25}$$

因此, 通过施加与腿长 成比例的踢力 , CoM 在约束线上移动 (此外, 我们还需要与约束相匹配的初始条件) . 这种钟摆运动如图 4.12 所示. 图中箭头表示踢力的大小和方向.

让我们来看看在这种控制下 CoM 的动力学特性. 将 (4.25) 代入 (4.21), 并应用 , 即可得到 CoM 的水平动力学方程.

$$\ddot{x}=\frac{g}{z_c}x.\tag{4.26}$$

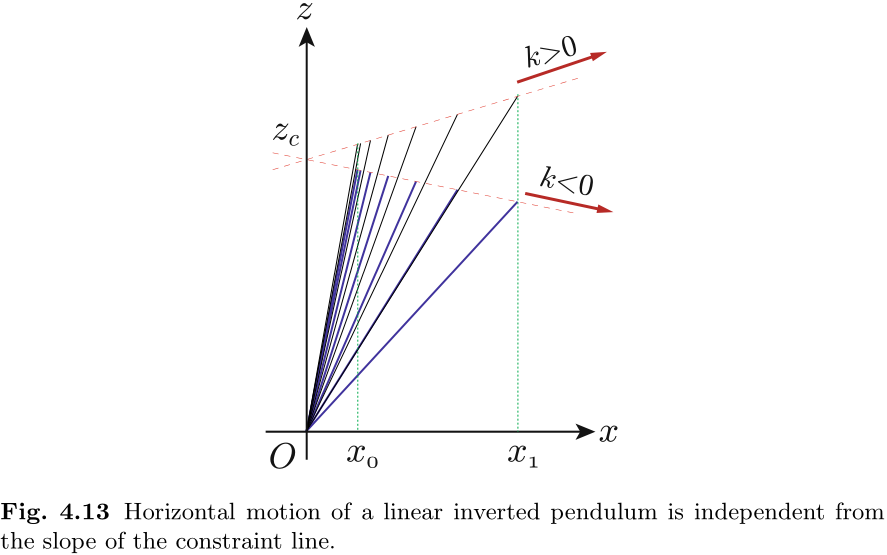
令人惊讶的是, 这与针对 CoM 水平运动得出的 (4.4) 完全相同！为了明确这一结果的含义, 我们在图 4.13 中展示了两个在不同约束线上运动的倒垂线的模拟结果. 两条约束线的斜率不同, 但交点 相同, 垂体从相同的水平位置 开始运动. 人们可能会认为, 在上升线上 (k > 0) 的摆会减速, 而在下降线上 (k < 0) 的摆会加速. 然而, 如图 4.13 所示, 两个摆锤的水平运动完全相同, 并且同时到达 . 这是因为重力效应被踢力抵消, 摆的运动只受 CoM 水平位置的影响.

利用这一事实, 我们可以很容易地设计出在不平坦地形上的行走模式. 图 4.14 显示了一个爬楼梯的规划示例. 首先, 我们设置适当的着陆点 (三角形) , 然后通过连接位于着陆点 高度的点来指定约束线. 通过控制 CoM 沿这些约束线移动, 我们可以得到每一步的 CoM 水平动力学方程.

$$\ddot{x}=\frac{g}{z_c}x.$$

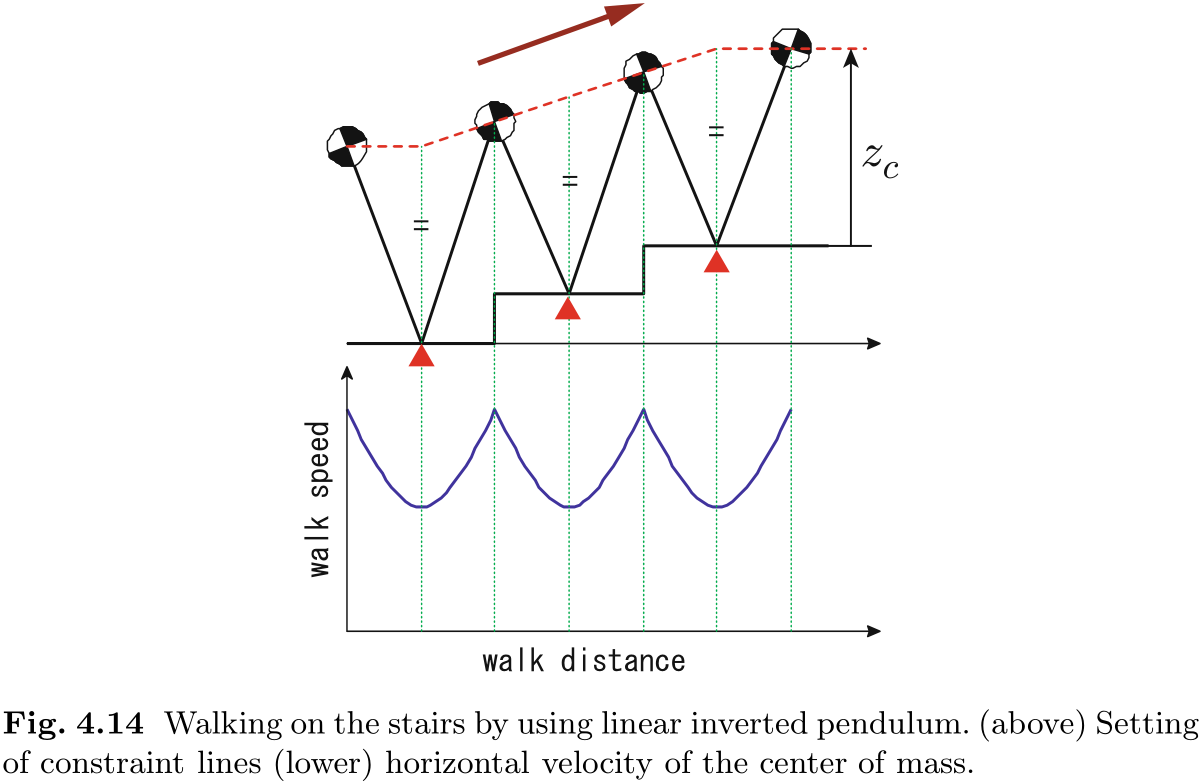
因此, 我们可以采用上一节的方法. 图 4.14 的下图表明, 爬楼梯不会影响 CoM 的水平速度.

通过这些方法, 我们可以轻松制作出各种地面几何形状的行走模式. 作者开发了一种简单的双足机器人 (图 4.15) , 它可以通过实时感应走过楼梯和障碍物 [116].

4.3 三维行走模式生成

在本节中, 我们将线性倒立摆扩展到三维, 并研究其本质. 利用三维线性倒立摆, 描述了三维行走模式的生成.

4.3.1 三维线性倒立摆

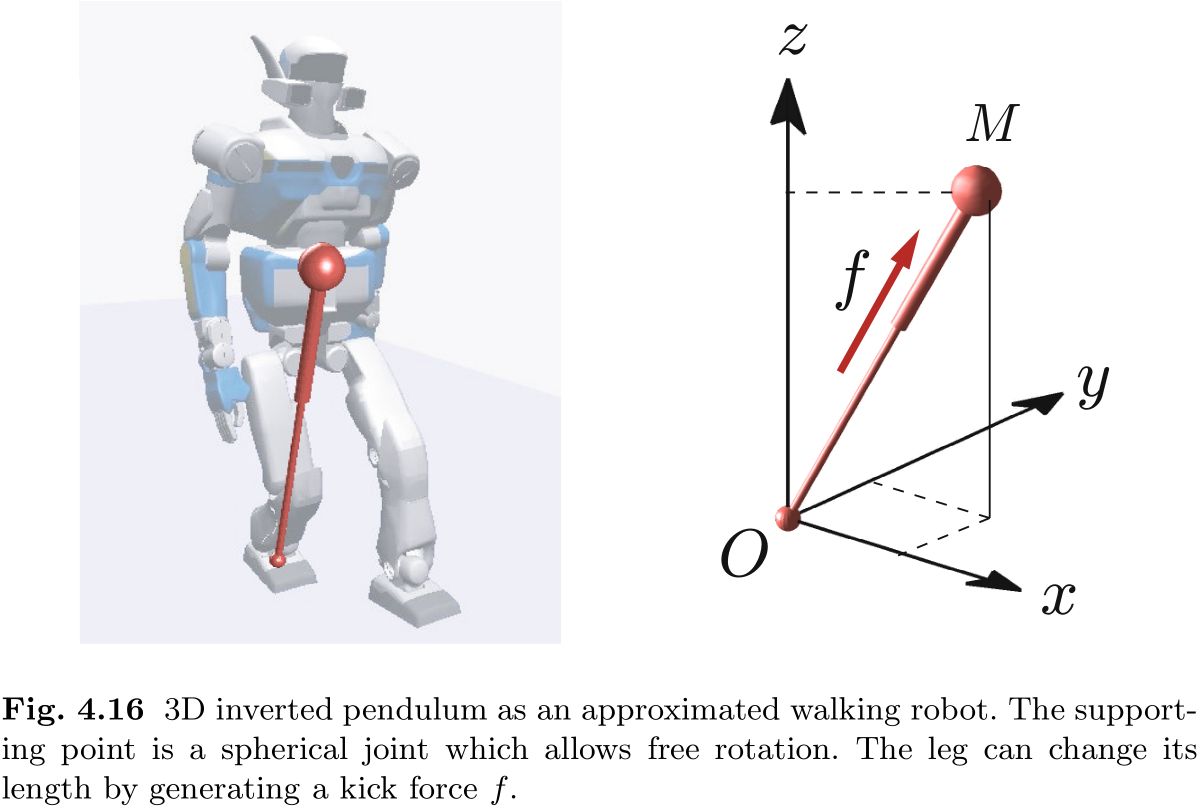
让我们将三维空间中的双足行走机器人近似为图 4.16 中的假想倒立摆, 它由机器人的 CoM 和连接 CoM 与支撑点的无质量腿组成. 我们假定摆锤可以围绕支撑点自由旋转, 腿可以通过踢力 改变长度. 我们可以将踢力 分解为三个分量, 即 , 和 .

$$f_x=(x/r)f\tag{4.27}$$ $$f_y=(y/r)f\tag{4.28}$$ $$f_z=(z/r)f\tag{4.29}$$

其中, 为支撑点与 CoM 之间的距离. 只有踢力和重力作用在 CoM 上, 因此 CoM 的运动方程为

$$M\ddot{x}=(x/r)f,\tag{4.30}$$ $$M\ddot{y}=(y/r)f,\tag{4.31}$$ $$M\ddot{z}=(z/r)f-Mg.\tag{4.32}$$

与处理二维倒立摆时一样, 我们来考虑一下 CoM 的约束. 对于三维倒立摆, 我们引入一个约束平面, 其定义为

$$z=k_xx+k_yy+z_c,\tag{4.33}$$

其中, , 决定坡度, 决定约束平面的高度.

要让 CoM 沿着这个平面移动, 我们需要它的加速度与约束条件的法向量正交. 因此, 我们需要

$$\begin{bmatrix} f(\frac{x}{r})&f(\frac{y}{r})&f(\frac{z}{r})-Mg \end{bmatrix}\begin{bmatrix} -k_x\\ -k_y\\ 1 \end{bmatrix}=0.\tag{4.34}$$

求解 的方程, 并代入 (4.33) 即可得出

$$f=\frac{Mgr}{z_c}.\tag{4.35}$$

通过施加与腿长 成比例的踢力 , 质心在约束平面上移动. 图 4.17 显示了这一运动的图像.

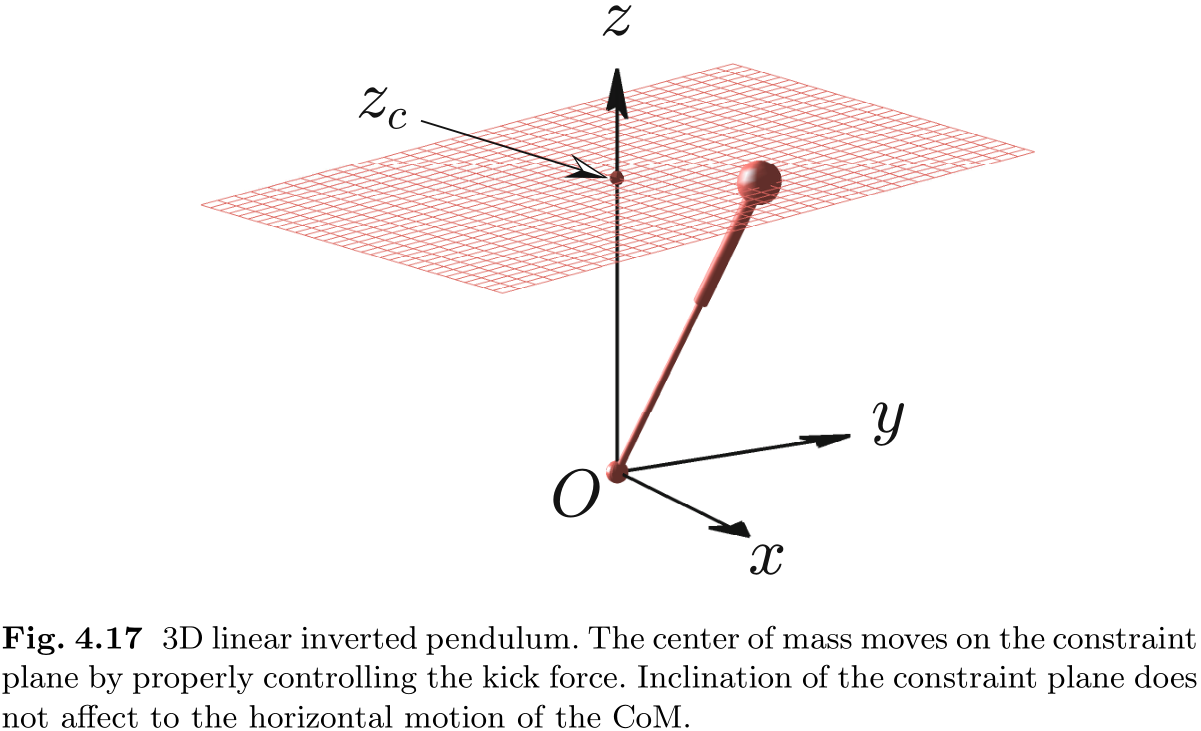
从 (4.30) 和 (4.31) 可以推导出 CoM 的水平动力学方程, 将 (4.35) 中的踢力代入即可得到

$$\ddot{x}=\frac{g}{z_c}x,\tag{4.36}$$ $$\ddot{y}=\frac{g}{z_c}y.\tag{4.37}$$

这些都是线性方程, 约束平面的交点 是唯一的参数. 约束平面的倾斜参数 , 不会影响 CoM 的水平运动, 因为它们不在 (4.36) 和 (4.37) 中. 我们称这种摆为三维线性倒立摆.

三维线性倒立摆最初由 Hara, Yokogawa 和 Sadao [59] 发现. Kajita, Matsumoto 和 Saigo [118] 对其进行了扩展, 将踝关节力矩考虑在内.

4.3.2 三维线性倒立摆的性质

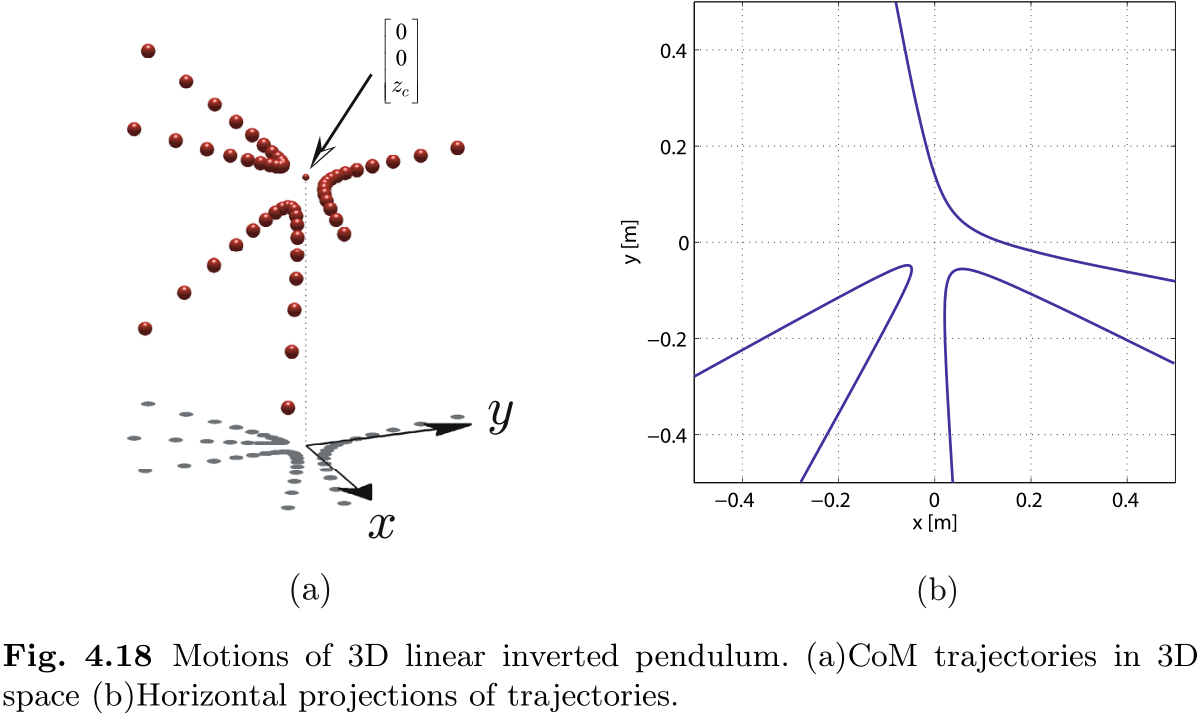
三维线性倒立摆虽然是两个二维线性倒立摆的组合, 但其本质更为有趣. 图 4.18 显示了三维线性倒立摆的三个轨迹, 其约束平面具有相同的 轴交点. 我们可以观察到以 轴交点 为焦点的令人印象深刻的彗星状轨迹. 我们可以忽略约束平面的倾斜度, 将这些三维轨迹的动态视为在 平面上的投影 (图 4.18(b)) .

LIP 的轨迹不同于绕太阳运行的彗星轨迹. 更恰当的比喻是卢瑟福散射实验中的粒子轨迹, 该实验证明了原子核的存在. 正如下文所示, 这的确是一个非常好的类比.

① 开普勒第二定律

根据天体力学的类比, 让我们来检验一下开普勒第二定律: 行星的速度是恒定的. 掠面速度 是单位时间内原点和 CoM 的连线所扫过的面积, 其值为

$$v_{area}=\frac{1}{2}(x\dot{y}-\dot{x}y).\tag{4.38}$$

我们可以对三维线性倒立摆的掠面速度时间导数进行如下检验

$$\begin{align*} \frac{d}{dt}(v_{area})&=\frac{1}{2}(\dot{x}\dot{y}+x\ddot{y}-\ddot{x}y-\dot{x}\dot{y})\\ &=\frac{1}{2}(x\ddot{y}-\ddot{x}y)\quad\leftarrow(\text{带入方程(4.36)和(4.37)})\\ &=\frac{1}{2}\left(x\frac{g}{z_h}y-\frac{g}{z_h}xy\right)\\ &=0. \end{align*}$$

因此, 三维线性倒立摆的掠面速度是恒定的.

一般来说, 在中心力场中的任何运动的掠面速度都是守恒的. 它以不同的方式表示角动量守恒.

② 参照系旋转

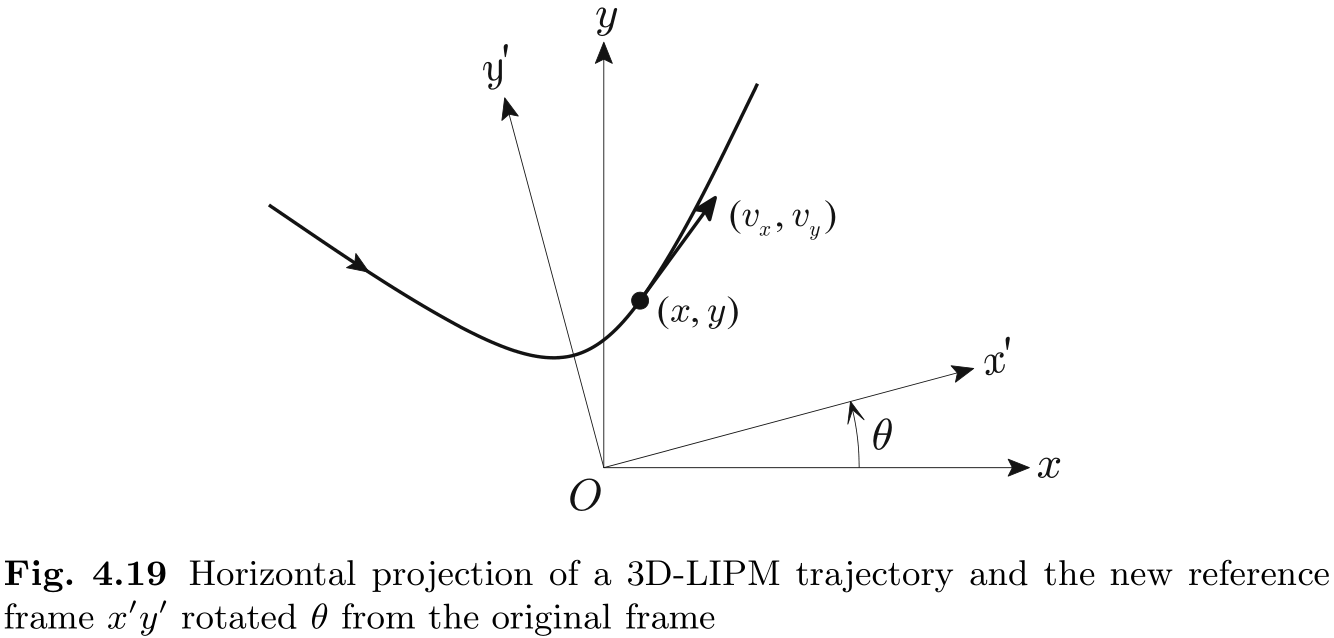
接下来, 我们考虑从原始参照系 到旋转 的新参照系 的坐标变换, 如图 4.19 所示. 变换为

$$x=cx'-sy',\tag{4.39}$$ $$y=sx'+cy',\tag{4.40}$$ $$c\equiv\cos\theta,s\equiv\sin\theta.$$

让我们确认三维线性倒立摆的方程 (4.36) 和 (4.37) 在新参照系 中仍然有效. 代入上述方程给出的坐标变换, 我们可以得到

$$c\ddot{x}'-s\ddot{y}'=\frac{g}{z_h}(cx'-sy'),\tag{4.41}$$ $$s\ddot{x}'+c\ddot{y}'=\frac{g}{z_h}(sx'+cy').\tag{4.42}$$

根据 和 , 我们可以得到在 参照系下的动力学方程, 即

$$\begin{align*} \ddot{x}'&=\frac{g}{z_c}x',\\ \ddot{y}'&=\frac{g}{z_c}y'. \end{align*}$$

对于任何给定的旋转角度 , 这种变换都是可能的. 因此, 我们已经证实, 三维线性倒立摆动力学总是可以分离成两个正交分量, 而不受参照系方向的影响.

在重力或静电力作用下的运动与距离的平方成反比, 不能这样处理.

③ 三维线性倒立摆轨迹的几何

我们可以利用图 4.19 的变换和轨道能量计算出轨迹的几何形状. 新坐标系沿 轴的轨道能量为

$$E_x'=-\frac{g}{2z_c}(cx+sy)^2+\frac{1}{2}(c\dot{x}+s\dot{y})^2.\tag{4.43}$$

当 或 与轨迹的对称轴相对应时, 轨道能量 将达到极值. 从

$$\frac{\partial E_x'}{\partial\theta}=-A\cos2\theta+\frac{B}{2}\sin2\theta=0\tag{4.44}$$ $$\begin{align*} A&\equiv(g/z_c)xy-\dot{x}\dot{y}\\ B&\equiv(g/z_c)(x^2-y^2)-(\dot{x}^2-\dot{y}^2) \end{align*}$$

我们可以计算出表示轨迹对称轴的 .

$$\theta=\left\{\begin{align*} &(1/2)\tan^{-1}(2A/B) &(\text{if }B\ne0)\\ &\pi/4 &(\text{if }A\ne0,B=0) \end{align*}\right.\tag{4.45}$$

在 的情况下, 轨迹变成了一条朝向原点的直线或一条从原点出发的直线, 而这条直线本身就是一条对称轴.

假设我们已经选择了符合对称轴的 轴. 在这种情况下, 轨道能量 必须取 的极值. 将 代入 (4.44) , 我们得到

$$(g/z_c)xy-\dot{x}\dot{y}=0.$$

将第二项转移到右边后, 我们将方程两边平方, 得到

$$(g/z_c)^2x^2y^2=\dot{x}^2\dot{y}^2.$$

我们将根据轨道能量的定义推导出的以下两个等式代入其中

$$\dot{x}^2=2E_x+\frac{g}{z_c}x^2\qquad\dot{y}^2=2E_y+\frac{g}{z_c}y^2$$

得出表示三维线性倒立摆轨迹几何形式的方程, 该方程为

$$\frac{g}{2z_cE_x}x^2+\frac{g}{2z_cE_y}y^2+1=0.\tag{4.46}$$

这是一个双曲线方程, 因为 中的一个是负数, 另一个是正数.

在卢瑟福散射或旅行者一号和二号等航天器的摆动轨迹中可以观察到双曲线轨迹. 在基本粒子, 行星空间和双足运动中发现类似轨迹, 我感到非常兴奋. 难道不是吗?

4.3.3 三维行走模式生成

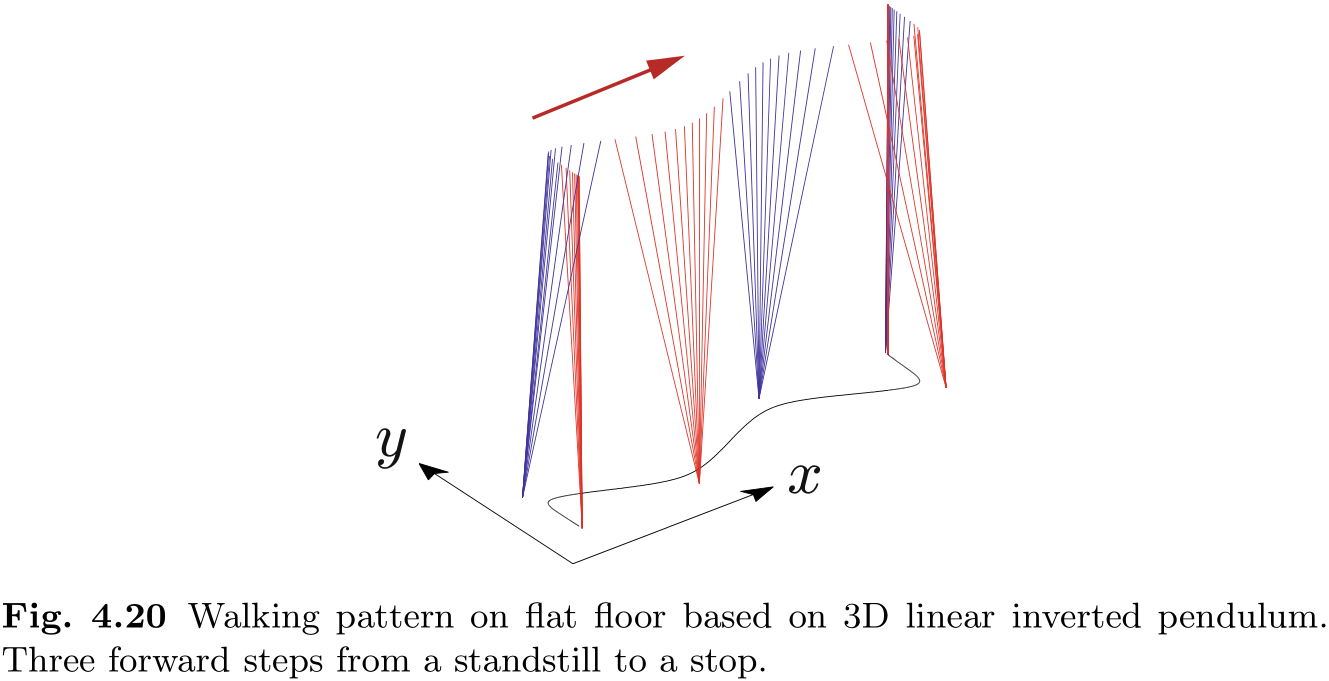
图 4.20 展示了一个基于三维线性倒立摆的行走模式示例. 通过设置适当的约束平面, 我们可以在楼梯或不平的地面上应用相同的模式.

对于三维行走, 我们需要在 和 方向上同时进行支撑交换, 因此我们不能使用第 4.2.5 节中阐述的行走模式生成方法, 该方法需要任意的支撑交换时间. 在下面的讨论中, 我们考虑以恒定的支撑交换速度行走, 并用 表示每一步的支撑周期.

① 行走基元

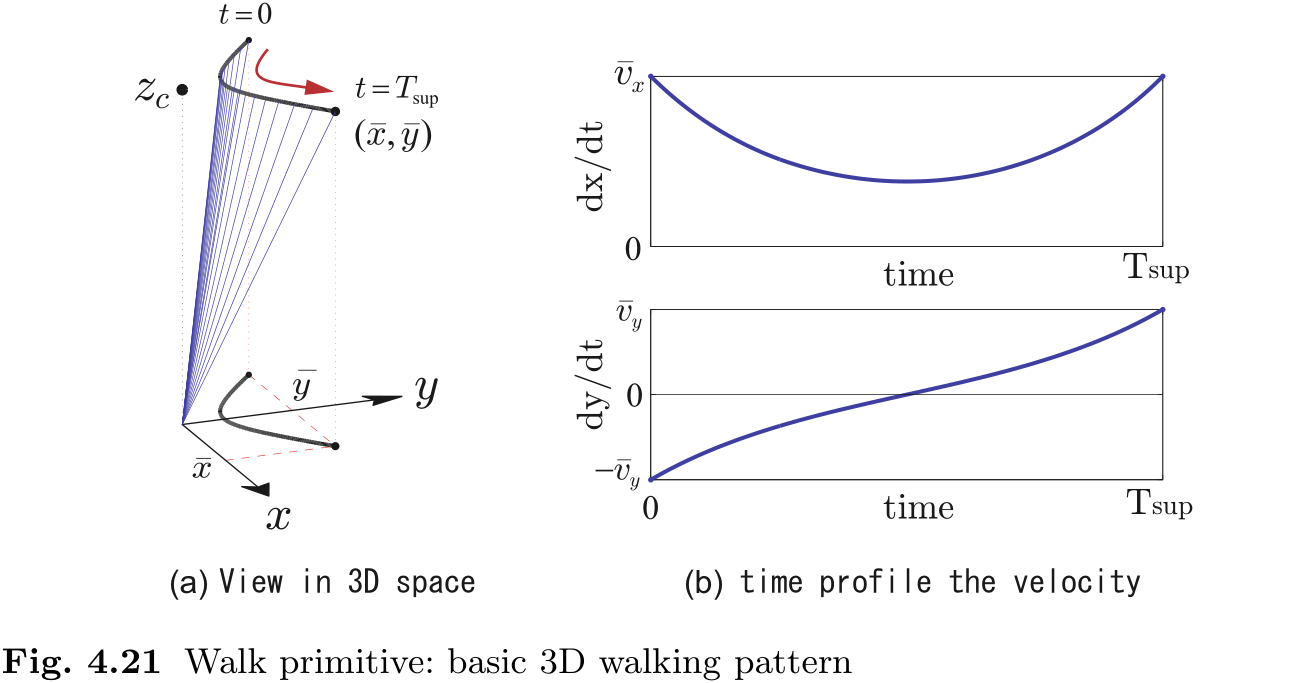
让我们定义一段三维线性倒立摆轨迹, 如图 4.21 所示, 该轨迹绕 轴对称, 周期为 . 如前所述, 图 4.21(a) 是双曲线的一部分. 我们称这一段轨迹为行走基元 (walk primitive) .

当给定支持时间 和约束平面 的交点时, 由于步行基元是对称的, 因此它的终点位置 是唯一确定的. 终点速度 的计算公式如下.

利用行走基元的对称性, 沿 轴的初始条件为 , 终点位置为 . 根据线性倒立摆的解析解 (4.5), 我们可以得出

$$\bar{x}=-\bar{x}C+T_c\bar{v}_xS,\tag{4.47}$$

其中

$$T_c\equiv\sqrt{\frac{z_c}{g}},\quad C\equiv\cosh\frac{T_{sup}}{T_c},\quad S\equiv\sinh\frac{T_{sup}}{T_c}.$$

求解 (4.47) 的末端速度 得到

$$\bar{v}_x=\bar{x}(C+1)/(T_cS).\tag{4.48}$$

同样, 对于行走原点的 分量, 初始条件为 , 终点位置为 , 因此我们得到的终点速度为

$$\begin{align*} \bar{y}&=\bar{y}C+T_c(-\bar{v}_y)S,\\ \bar{v}_y&=\bar{y}(C-1)/(T_cS). \end{align*}\tag{4.49}$$

通过行走基元, 我们可以轻松制作出行走轨迹. 例如, 通过连接相同的行走基元, 并在每次接触后反转 分量的符号, 就能产生步长为 的直线行走.

② 行走参数

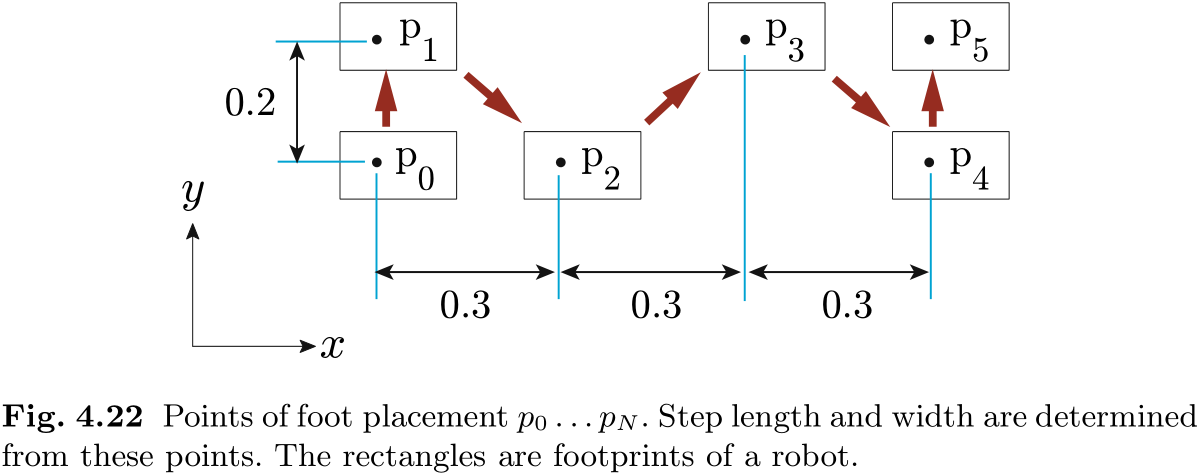
在爬楼梯或躲避障碍物等实际情况下, 经常需要直接指定脚的位置. 图 4.22 展示了一个简单的脚部位置示例, 可以用以下数据作为步长和步宽来表示.

其中, 为沿行走方向的步长, 为横向的步宽. 我们称这些数据为行走参数, 因为它编码了图 4.22 中的脚部位置. 用上标 表示第 步的数据, 则第 个落脚点 可表示为

$$\begin{bmatrix} p_x^{(n)}\\ p_y^{(n)} \end{bmatrix}=\begin{bmatrix} p_x^{(n-1)}+s_x^{(n)}\\ p_y^{(n-1)}-(-1)^ns_y^{(n)} \end{bmatrix},\tag{4.50}$$

其中 是第一只支撑脚的位置, 在本例中是右脚. 如果第一只支撑脚是左脚, 我们必须在等式中用 代替 .

第 步的行走基元可按以下方式确定

$$\begin{bmatrix} \bar{x}^{(n)}\\ \bar{y}^{(n)} \end{bmatrix}=\begin{bmatrix} s_x^{(n+1)}/2\\ (-1)^ns_y^{(n+1)}/2 \end{bmatrix}.\tag{4.51}$$

请注意, 第 步的行走原始步长由第 步的步长和步幅决定. 这对于正确协调脚的位置和行走动作是必要的.

行走基元的末端速度由 (4.48) 和 (4.49) 计算得出

$$\begin{bmatrix} \bar{v}_x^{(n)}\\ \bar{v}_y^{(n)} \end{bmatrix}=\begin{bmatrix} (C+1)/(T_cS)\bar{x}^{(n)}\\ (C-1)/(T_cS)\bar{y}^{(n)} \end{bmatrix}.\tag{4.52}$$

用这种方法确定的一系列行走基元在一组步伐的开始和结束处是不连续的. 下一节将阐述获得连续且可实现的行走模式的方法.

③ 修改脚部位置

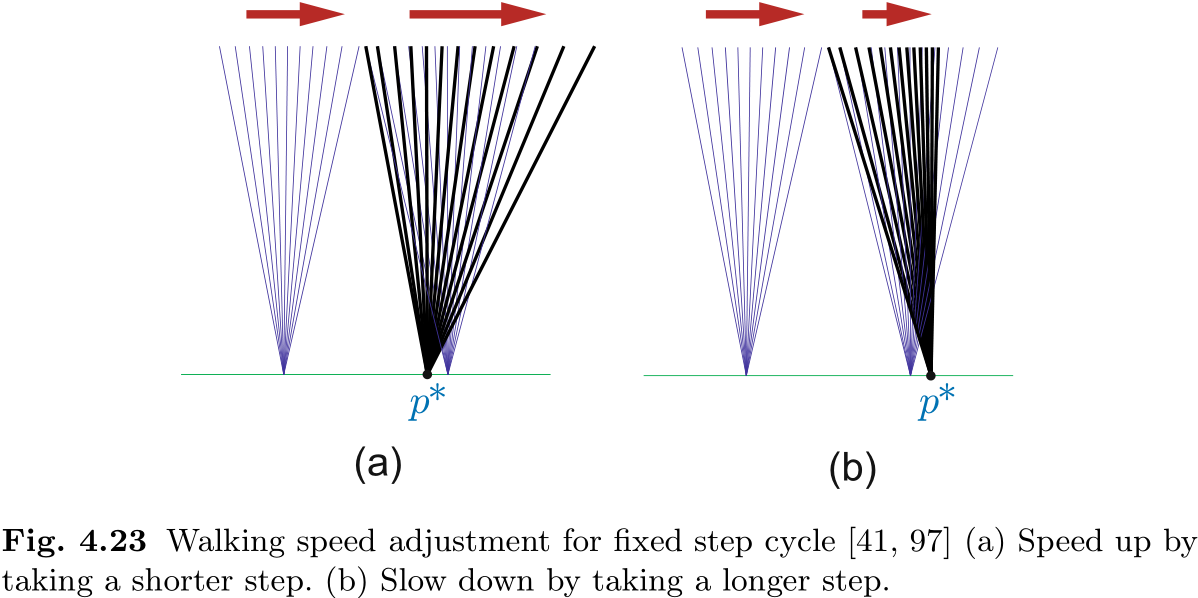
对于以固定步周期行走的机器人, 我们可以通过调整脚的位置来控制其速度. 其直观的解释如图 4.23 所示.

在图 4.7 (第 114 页) 的控制方法中, 步长是固定的, 行走速度则通过修改触地时间来控制.

我们将修改后的脚部位置记为 , 并计算其对行走运动的影响. 图 4.24 展示了一个相对于地面固定参照系的线性倒立摆,

$$\ddot{x}=\frac{g}{z_c}(x-p_x^*).\tag{4.53}$$

我们只讨论沿 轴的运动, 但沿 轴的运动也会得到同样的结果.

其解析解为

$$x(t)=\left(x_i^{(n)}-p_x^*\right)\cosh(t/T_c)+T_c\dot{x}_i^{(n)}\sinh(t/T_c)+p_x^*,\tag{4.54}$$ $$\dot{x}(t)=\frac{x_i^{(n)}-p_x^*}{T_c}\sinh(t/T_c)+\dot{x}_i^{(n)}\cosh(t/T_c),\tag{4.55}$$

其中, 为第 步开始时的初始条件.

因此, 脚的位置 与第 步的最终状态之间的关系为

$$\begin{bmatrix} x_f^{(n)}\\ \dot{x}_f^{(n)} \end{bmatrix}=\begin{bmatrix} C & T_cS\\ S/T_c & C \end{bmatrix}\begin{bmatrix} x_i^{(n)}\\ \dot{x}_i^{(n)} \end{bmatrix}+\begin{bmatrix} 1-C\\ -S/T_c \end{bmatrix}p_x^*.\tag{4.56}$$

作为目标状态, 我们使用地面帧中呈现的行走基元的最终状态

$$\begin{bmatrix} x^d\\ \dot{x}^d \end{bmatrix}=\begin{bmatrix} p_x^{(n)}+\bar{x}^{(n)}\\ \bar{v}_x^{(n)} \end{bmatrix}.\tag{4.57}$$

让我们计算最终状态最接近目标 的脚的位置. 评估函数可定义为

$$N\equiv a\left(x^d-x_f^{(n)}\right)^2+b\left(\dot{x}^d-\dot{x}_f^{(n)}\right)^2\tag{4.58}$$

其中 为正权重. 将 (4.56) 代入评价函数, 并使用 , 我们就能得到使 最小化的脚部位置

$$\begin{align*} p_x^*= &-\frac{a(C-1)}{D}\left(x^d-Cx_i^{(n)}-T_cS\dot{x}_i^{(n)}\right)\\ &-\frac{bS}{T_cD}\left(\dot{x}^d-\frac{S}{T_c}x_i^{(n)}-C\dot{x}_i^{(n)}\right)\\ D\equiv &\space a(C-1)^2+b(S/T_c)^2. \end{align*}\tag{4.59}$$

行走模式的生成方法可以组织成一个算法, 如图 4.25 所示.

• 图 4.25 基于 3D-LIP 的行走模式生成算法
  • 步骤 1: 设置支撑周期 和行走参数 . 设置 CoM 的初始位置 和初始脚的位置 ;
  • 步骤 2: ;
  • 步骤 3: 积分从 到 的线性倒立摆方程 (4.53) (以及 轴方程) ;
  • 步骤 4: ;
  • 步骤 5: 利用 (4.50) 计算下一个落脚点 ;
  • 步骤 6: 利用 (4.51) 和 (4.52) 设置下一个行走基元 ;
  • 步骤 7: 根据 (4.57) 计算目标状态 , 根据相应公式计算目标状态 ;
  • 步骤 8: 根据 (4.59) (以及 分量) 计算修改后的脚位 ;
  • 步骤 9: 转至步骤 3.

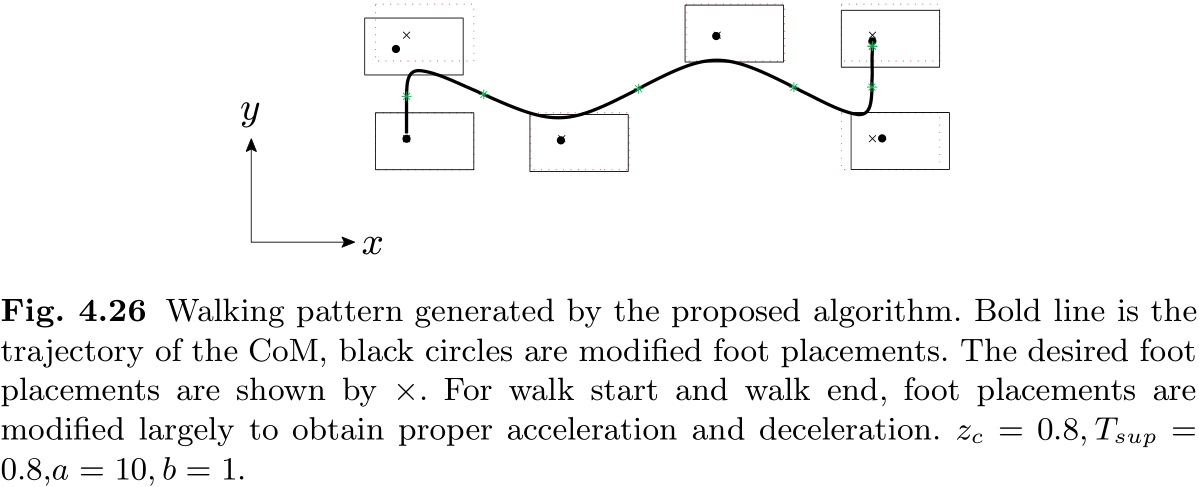
图 4.26 显示了根据图 4.22 的行走参数生成的行走模式. 我们可以观察到, 在行走开始时, 脚步略微后退以获得加速度, 而在行走结束时, 脚步略微加宽以获得减速度. 由于需要对脚部位置进行这样的调整, 因此这种方法无法实现行走参数指定的精确脚部位置. 不过, 由于 (4.59) 可以保证误差趋于零, 因此机器人可以在稳定行走时采取指定的脚部位置.

对于对角线行走, 我们每走一步都要改变 .

图 4.27 显示了这组行走参数产生的模式. 如果我们将这组参数中的所有 设为零, 就可以实现纯侧向行走.

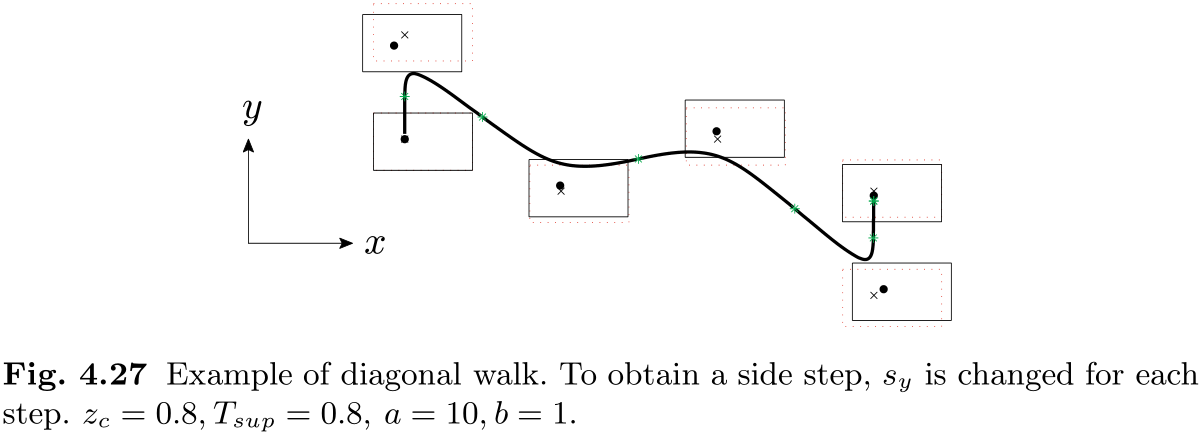
④ 改变行走方向

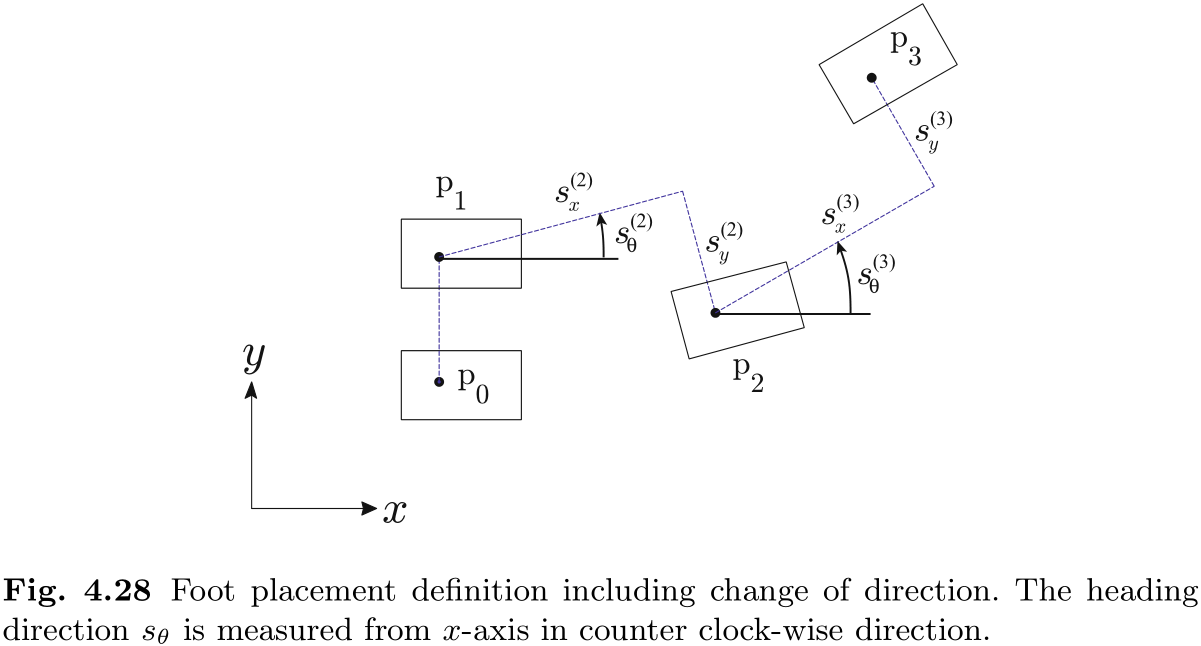
为了改变行走方向, 我们需要在行走参数中添加朝向信息. 如图 4.28 所示, 一步的方向变化用 表示.

这个定义比我们现在使用的方法要简单一些. 例如, 这种方法不能在原地产生步进式转弯. 至于如何找到更好的定义, 就需要读者自己去探索了.

第 步的脚部位置 由以下公式确定

$$\begin{bmatrix} p_x^{(n)}\\ p_y^{(n)} \end{bmatrix}=\begin{bmatrix} p_x^{(n-1)}\\ p_y^{(n-1)} \end{bmatrix}+\begin{bmatrix} \cos s_\theta^{(n)} & -\sin s_\theta^{(n)}\\ \sin s_\theta^{(n)} & \cos s_\theta^{(n)} \end{bmatrix}\begin{bmatrix} s_x^{(n)}\\ -(-1)^ns_y^{(n)} \end{bmatrix}.\tag{4.60}$$

第 n 步的行走基元为

$$\begin{bmatrix} \bar{x}^{(n)}\\ \bar{x}^{(n)} \end{bmatrix}=\begin{bmatrix} \cos s_\theta^{(n+1)} & -\sin s_\theta^{(n+1)}\\ \sin s_\theta^{(n+1)} & \cos s_\theta^{(n+1)} \end{bmatrix}\begin{bmatrix} s_x^{(n+1)}/2\\ (-1)^ns_y^{(n+1)}/2 \end{bmatrix}.\tag{4.61}$$

行走基元的速度计算公式也是

$$\begin{bmatrix} \bar{v}_x^{(n)}\\ \bar{v}_y^{(n)} \end{bmatrix}=\begin{bmatrix} \cos s_\theta^{(n+1)} & -\sin s_\theta^{(n+1)}\\ \sin s_\theta^{(n+1)} & \cos s_\theta^{(n+1)} \end{bmatrix}\begin{bmatrix} (1+C)/(T_cS)\bar{x}^{(n)}\\ (C-1)/(T_cS)\bar{y}^{(n)} \end{bmatrix}.\tag{4.62}$$

在行走模式生成算法步骤 5 中使用 (4.60) 代替 (4.50) , 在步骤 6 中使用 (4.61) 和 (4.62) 代替 (4.51) 和 (4.51) , 就可以生成具有任意方向控制的行走模式.

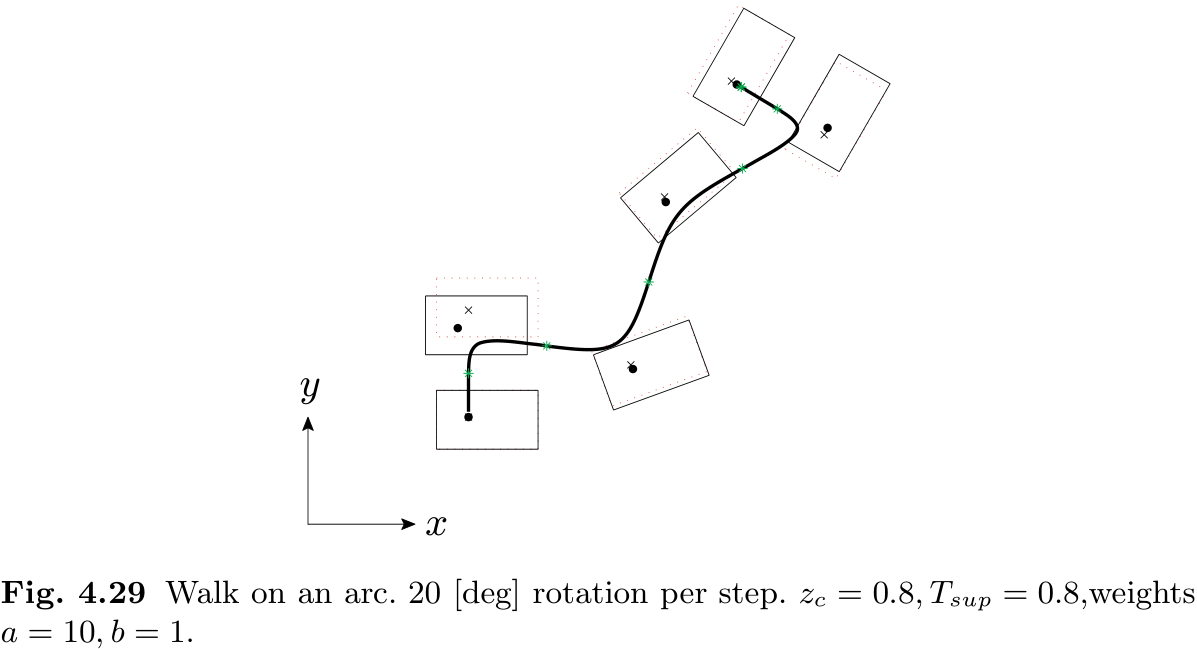
例如, 要在弧线上行走, 我们可以使用以下参数, 规定每一步旋转 20 [deg].

图 4.29 显示了根据该行走参数生成的行走轨迹.

4.3.4 引入双支撑阶段

到目前为止, 我们一直假设倒立摆模型的支撑腿是瞬时交换的. 然而, 这种突然的支撑腿交换会导致水平加速度从最大值跳到最小值, 如图 4.30(a) 所示. 因此, 机器人可能会受到巨大的冲击, 并有可能损坏.

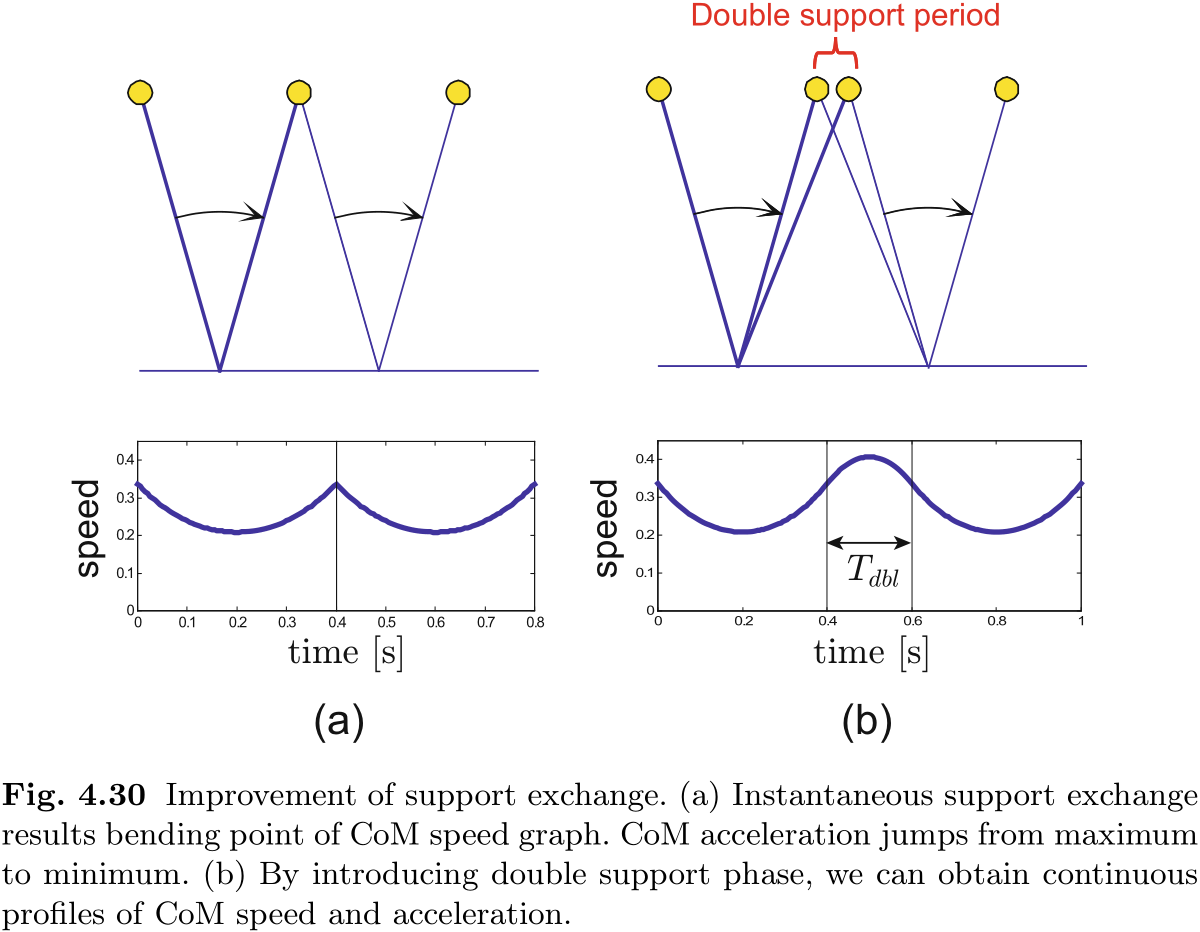
为了获得适合真实机器人的更平滑的行走模式, 在交换支撑腿的瞬间插入了一个具有预定周期 的双支撑阶段.

我们需要的是没有斜率突变的平滑速度曲线. 通过这种运动, 我们可以避免加速度的不连续变化, 从而使 ZMP 从前支撑脚平稳地转移到新支撑脚. 为此, 我们使用三阶多项式生成速度曲线, 从而可以指定双支撑周期开始和结束时的速度和加速度. 因此, CoM 的位置由四阶多项式描述 (图 4.30(b))

$$x(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4.\tag{4.63}$$

系数 取决于交换支撑腿瞬间 CoM 的位置, 速度和加速度.

引入双支撑后, 机器人的步长会大于计划步长. 这可以通过提前按比例减少行走基元来弥补. 图 4.31 显示了双支撑阶段的行走轨迹示例.

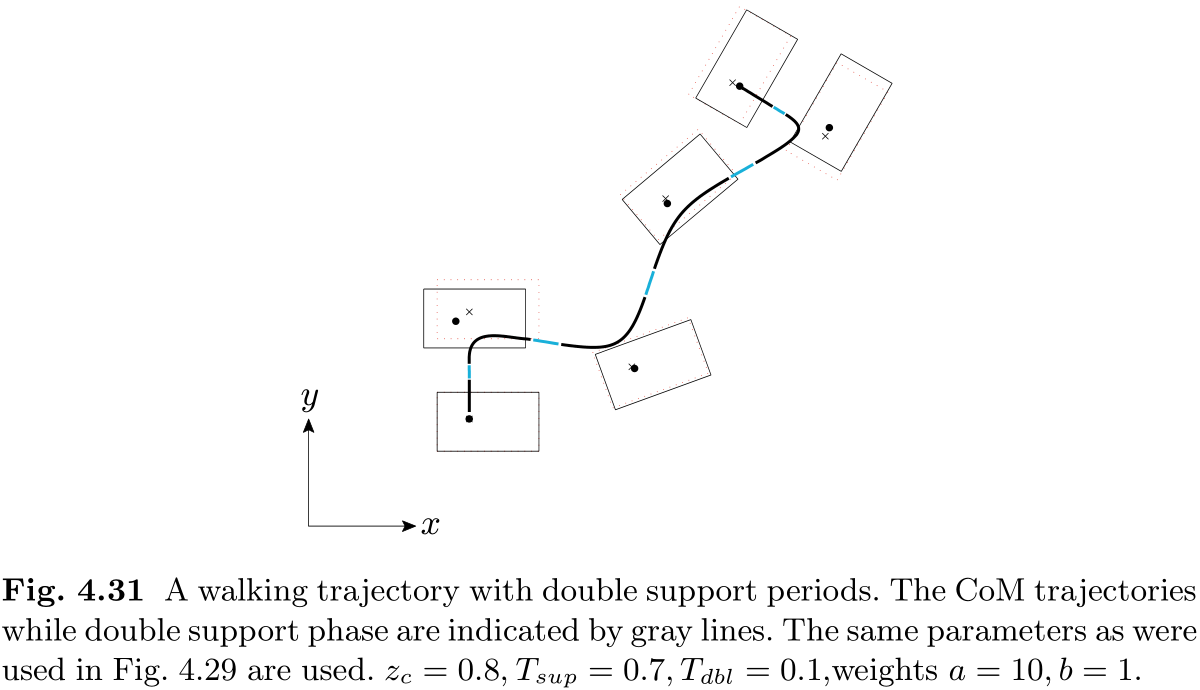
值得注意的是, 虽然较长的双支撑时间会使支撑交换更顺畅, 但也需要更快的摆动腿运动, 这是不可取的. 因此, 我们在确定 时需要权衡利弊.

4.3.5 从线性倒立摆到多体模型

利用线性倒立摆生成行走模式的最简单方法是让骨盆链节跟随 LIP 的 CoM 运动. 首先, 使用多体模型计算 CoM 的实际位置, 并确定其相对于骨盆参照系的位置. 之后, 假定 CoM 相对于骨盆的相对位置保持不变, 则直接根据线性倒立摆确定骨盆链节的位置. 此外, 我们还必须计算摆动脚的轨迹, 使其在指定的触地时间到达所需的脚部位置.

一旦我们确定了骨盆和双脚的运动轨迹, 就可以按照第 2 章中的解释, 通过逆运动学方法获得腿部关节角度.

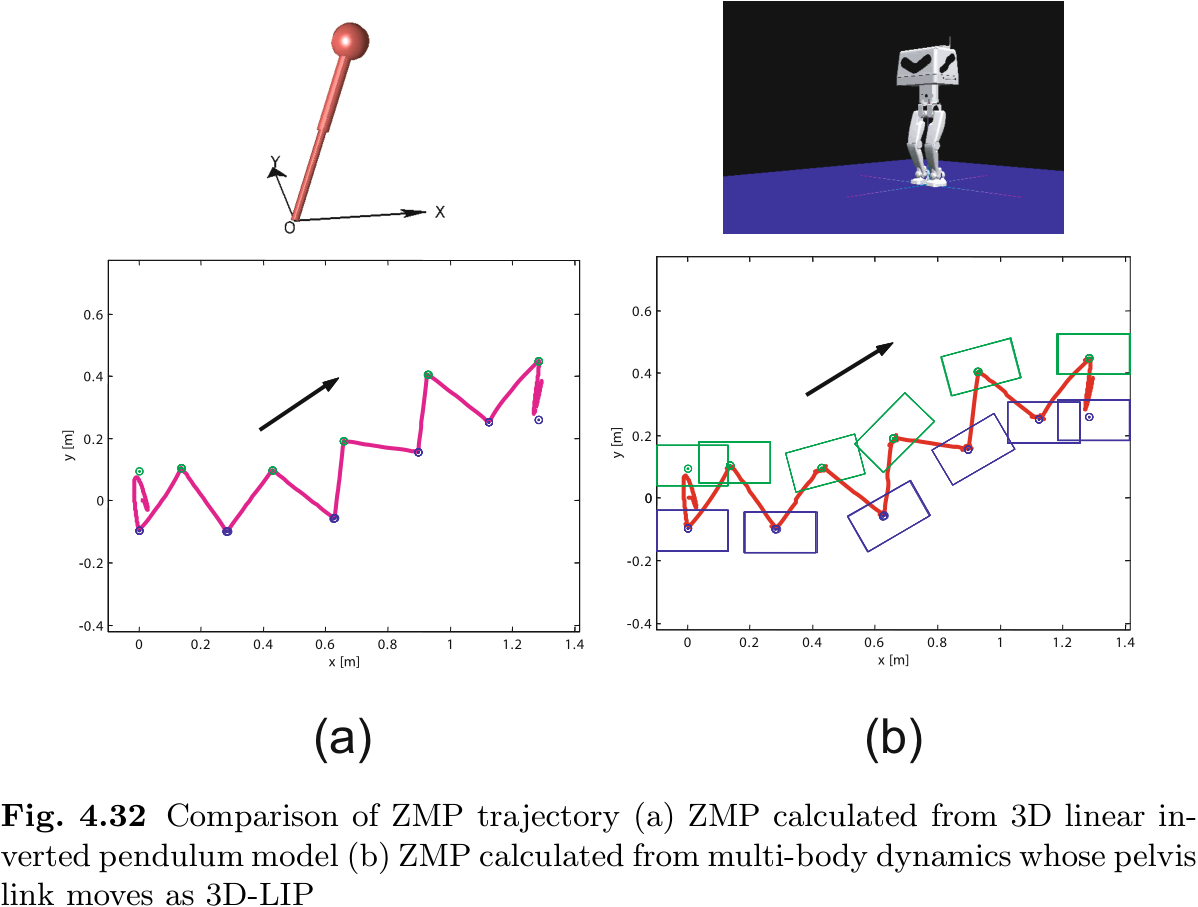
这种方法基于一个假设, 即机器人的多体动力学可以用一个简单的倒立摆来近似, 其有效性可以通过使用前一章所述的 ZMP 来确认. 通过使用多体模型计算 ZMP, 我们可以评估在线性倒立摆中被忽略的摆动腿反作用力和 CoM 位置误差的影响. 图 4.32 显示了两个 ZMP, 一个基于线性倒立摆, 另一个基于多体动力学及其模式生成. 两个 ZMP 都非常接近, 因此我们可以得出结论, 在这种情况下, 多体动力学可以简化为简单的倒立摆.

4.3.6 实施示例

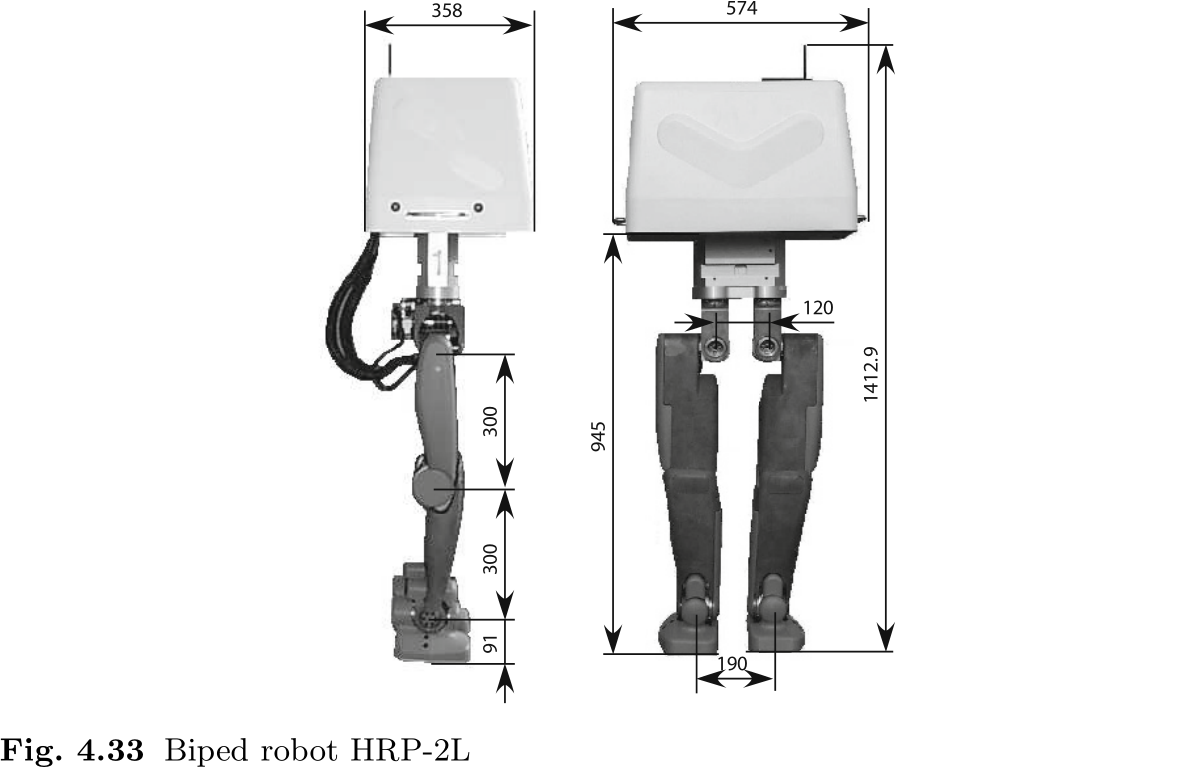
让我们来看看所提出的行走模式生成的实现. 图 4.33 显示了 "仿人机器人项目" (HRP) 开发的双足机器人 HRP-2L. 该机器人是为了评估人形机器人 HRP-2 的腿部而制造的, HRP-2 是该项目的最终目标. 每条腿都有六个自由度, 机器人的身体部分配备了基于奔腾 II 933MHz 的板载计算机.

图 4.25 中的算法可以生成至少两个未来步数的行走模式. 因此, 我们可以建立一个行走控制系统, 通过操纵杆指定未来两步的行走参数 来实时修改步数. 图 4.34 显示了我们的实时行走控制实验快照.

4.4 基于 ZMP 的行走模式生成

4.4.1 Cart-Table 模型

让我们考虑一下图 4.35 所示的新模型. 在这里, 质量为 M 的小车在质量小得可以忽略不计的桌子上行驶. 虽然桌脚太小, 无法让小车在桌边保持平衡, 但如果小车以一定的加速度运行, 桌脚仍能保持瞬时平衡. 我们称之为 Cart-Table 模型.

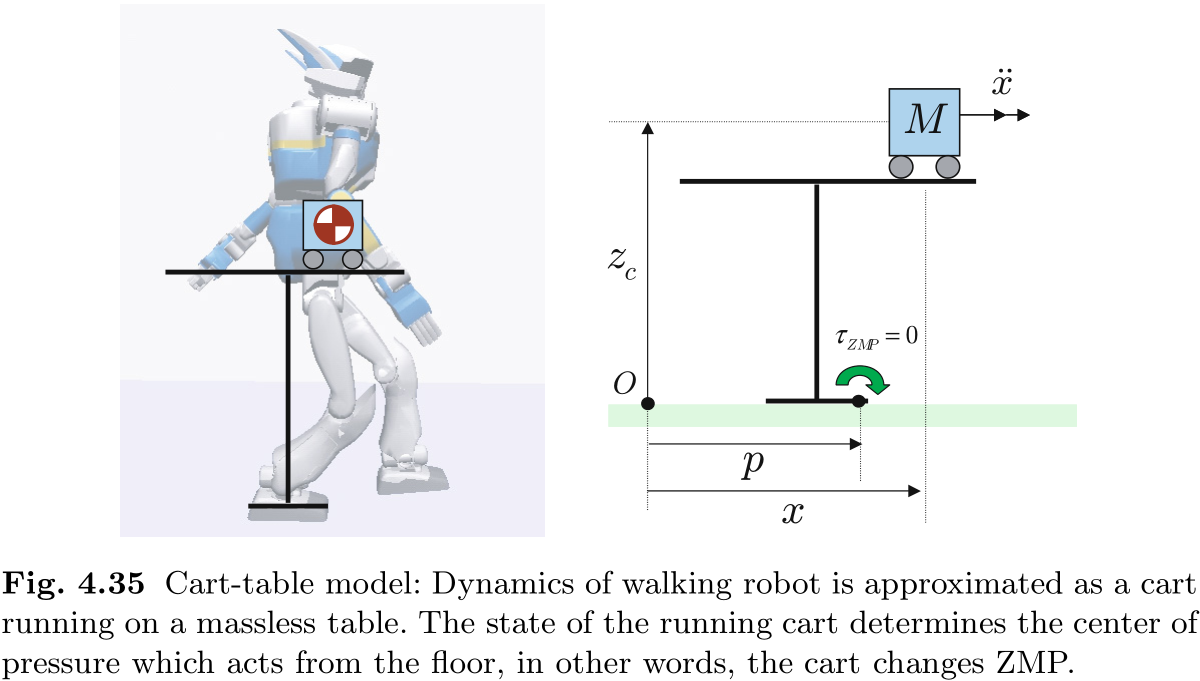
由于 Cart-Table 模型对应于第 3.5.2 节中高度不变的单个质点, 因此 ZMP 的计算公式为

$$p=x-\frac{z_c}{g}\ddot{x}.\tag{4.64}$$

我们称这个方程为 ZMP 方程.

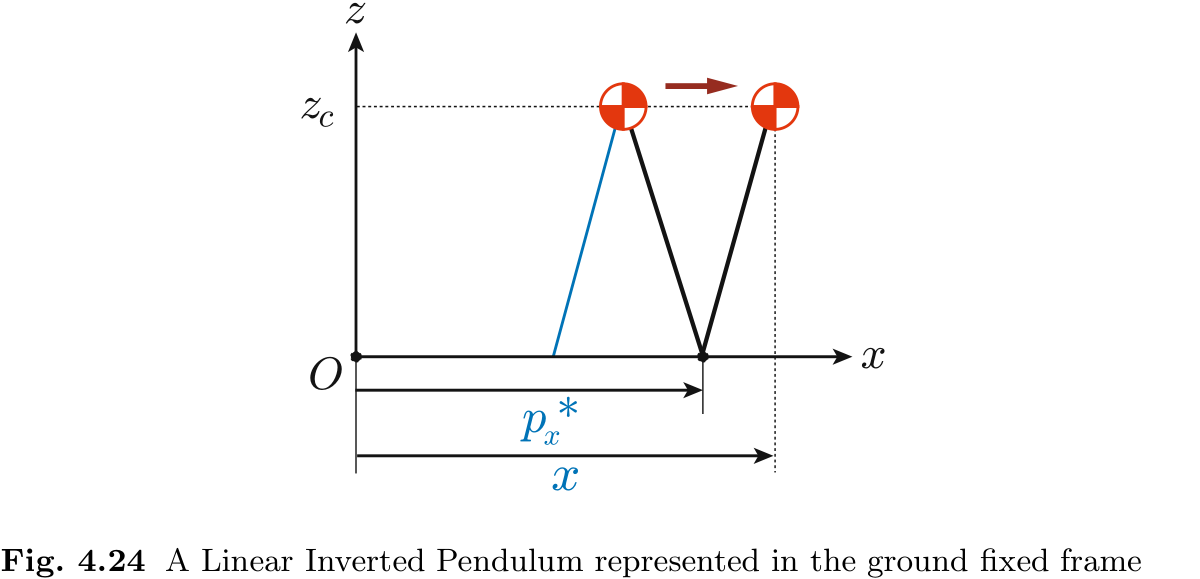
另一方面, 线性倒立摆的方程如下 (图 4.24)

$$\ddot{x}=\frac{g}{z_c}(x-p).\tag{4.65}$$

将 视为 ZMP, 而不是之前的脚部位置点, 我们就可以统一处理施加踝关节力矩的机器人和处于双支撑阶段的机器人 [134]. 此外, 我们还可以看到, (4.64) 和 (4.65) 是具有不同观点的相同方程.

图 4.36 比较了线性倒立摆模型和 cart-table 模型. 在线性倒立摆模型中, CoM 运动由 ZMP 产生 (图 4.36(a)) , 而在 cart-table 模型中, ZMP 由 CoM 运动产生 (图 4.36(b)) . 因此, 这两个模型具有相反的输入-输出因果关系.

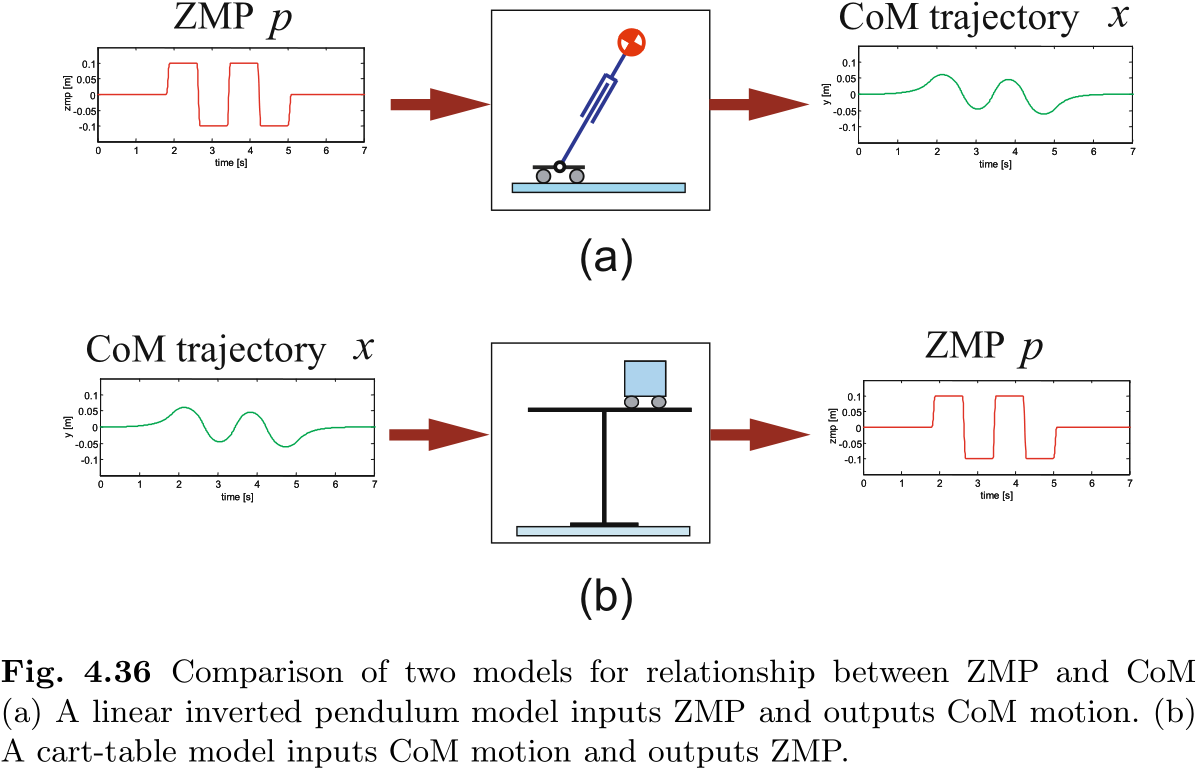
如前所述, 基于线性倒立摆的方法假定了图 4.36 (a) 中的输入输出关系, 并通过以下过程计算出行走模式.

$$\text{(指定目标 CoM 运动)}\Rightarrow\text{(计算适当的 ZMP)}$$

在这种情况下, 很难按预期规划 ZMP. 事实上, 我们已经按照上一节的方法修改了 ZMP (支撑脚位置) .

现在, 让我们考虑一下基于 cart-table 模型的行走模式生成. 在这种情况下, 假设存在图 4.36(b) 中的因果关系, 我们可以通过以下方式计算行走模式.

$$\text{(指定目标 ZMP 运动轨迹)}\Rightarrow\text{(计算适当的 CoM 运动)}$$

要实现给定的 ZMP 轨迹, 可能存在无限多的 CoM 运动, 但几乎所有运动都会产生分歧. 图 4.36(b) 可视为一种保证可执行解的机制.

这样, 我们就能得到实现指定 ZMP 轨迹的行走模式. 我们称这种方法为基于 ZMP 的行走模式生成法.

4.4.2 离线行走模式生成

Vukobratović 和 Stepanenko 在 1972 年发表的论文[90] 中首次提出了基于 ZMP 的行走模式生成方法, 但他们的算法需要耗费大量计算时间. 随后, Takanishi 等人提出了一种实用方法, 即通过 FFT 将目标 ZMP 模式转换为傅里叶级数, 在频域内求解 ZMP 方程 (4.64), 并通过反 FFT 得到 CoM 轨迹[11]. 基于这种方法的模式发生器在仿人机器人项目的早期阶段发挥了特别重要的作用.

后来, Takanishi 的方法被扩展用于处理实时模式生成 [40].

在本节中, 我们将介绍 Nishiwaki 等人最近提出的一种快速高效算法[114].

Nagasaka [93] 提出了另一种快速高效的方法.

让我们以采样时间 对 ZMP 方程进行离散化. 为此, 加速度 近似为

$$\ddot{x}_i=\frac{x_{i-1}-2x_i+x_{i+1}}{\Delta t^2},\tag{4.66}$$

其中 . 利用这一近似值, 离散化的 ZMP 方程为

$$\begin{align*} p_i&=ax_{i-1}+bx_i+cx_{i+1},\\ a_i&\equiv-z_c/(g\Delta t^2),\\ b_i&\equiv2z_c/(g\Delta t^2)+1,\\ c_i&\equiv-z_c/(g\Delta t^2). \end{align*}\tag{4.67}$$

将方程 (4.67) 放在指定周期 的一列中, 并将其表示为一个单一的矩阵方程, 得出

$$\begin{bmatrix} p_1'\\ p2\\ \vdots\\ p_{N-1}\\ p_N' \end{bmatrix}=\begin{bmatrix} a_1+b_1 & c_1 & 0 & & & & \\ a_2 & b_2 & c_2 & \ddots & & & \\ & & & \ddots & & & \\ & & & \ddots & a_{N-1} & b_{N-1} & c_{N-1}\\ & & & & 0 & a_N & b_N+c_N \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_{N-1}\\ x_N \end{bmatrix},\tag{4.68}$$

其中, 通过使用初始速度 和最终速度 来指定

$$p_1'=p_1+a_1v_1\Delta t,\qquad p_N'=p_N-c_Nv_N\Delta t.$$

将 (4.68) 重写为

$$\boldsymbol{p}=\boldsymbol{A}\boldsymbol{x}$$

并给出解的表示

$$\boldsymbol{x}=\boldsymbol{A}^{-1}\boldsymbol{p}.\tag{4.69}$$

虽然 是一个巨大的正方形矩阵, 有几千列和几千行, 但由于它是一个三对角矩阵, 除了主对角线和上下相邻的对角线外, 其他元素都是零, 因此存在一种计算逆的高效算法 [136].

根据此 CoM 轨迹, 我们可以利用第 4.3.5 节中的方法生成多体模型的行走模式. 然后, 我们就可以计算出多体模型的 ZMP 轨迹.

$$\boldsymbol{p}^*=\text{RealZMP}(\boldsymbol{x}).\tag{4.70}$$

函数 RealZMP() 根据多体模型计算 ZMP, $\boldsymbol{p}^\boldsymbol{p}^-\boldsymbol{p}^d$ 包含 cart-table 模型与多体模型之间的差异信息. 再利用 (4.69), 我们可以计算出补偿 ZMP 误差的 CoM 变量

$$\Delta\boldsymbol{x}=\boldsymbol{A}^{-1}(\boldsymbol{p}^*-\boldsymbol{p}^d).$$

CoM 轨迹更新为

$$\boldsymbol{x}:=\boldsymbol{x}-\Delta\boldsymbol{x}.$$

回到 (4.70), 我们可以重复同样的过程, 直到 ZMP 误差变得足够小.

这是一种非常高效的算法. 根据 Nishiwaki 等人的研究[73], 使用双 Pentium II 750MHz 的仿人机器人 H7 [113], 生成 32 DOF 的行走模式三步 (3.2 秒) 仅需 140 [ms]. 他们实现了操纵杆控制的实时行走, 方法是在每个步周期生成三个未来步, 并将它们正确连接起来.

4.4.3 在线行走模式生成

在本节中, 我们将介绍目前用于仿人机器人 HRP-2 的模式生成方法.

① ZMP 跟踪控制

如图 4.37 所示, 将 cart-table 模型作为一个动力系统, 可以想象一个通过反馈控制实现目标 ZMP 跟踪的伺服系统.

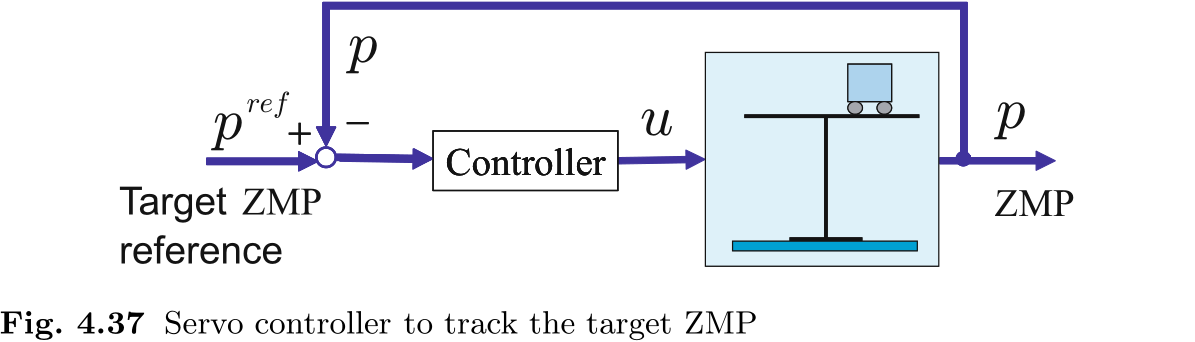
我们将推车加速度的导数 (jerk) 定义为系统输入, 在标准的现代控制理论框架内处理 cart-table 模型

$$u\equiv\dddot{x}.$$

利用这一输入, 我们可以将 ZMP 方程 (4.64) 重写为以下状态空间表示

$$\begin{align*} &\frac{d}{dt}\begin{bmatrix}x\\ \dot{x}\\ \ddot{x}\end{bmatrix}=\begin{bmatrix}0&1&0\\0&0&1\\0&0&0\end{bmatrix}\begin{bmatrix}x\\ \dot{x}\\ \ddot{x}\end{bmatrix}+\begin{bmatrix}0\\0\\1\end{bmatrix}u\\ &p=\begin{bmatrix}1&0&-\frac{z_c}{g}\end{bmatrix}\begin{bmatrix}x\\ \dot{x}\\ \ddot{x}\end{bmatrix}. \end{align*}\tag{4.71}$$

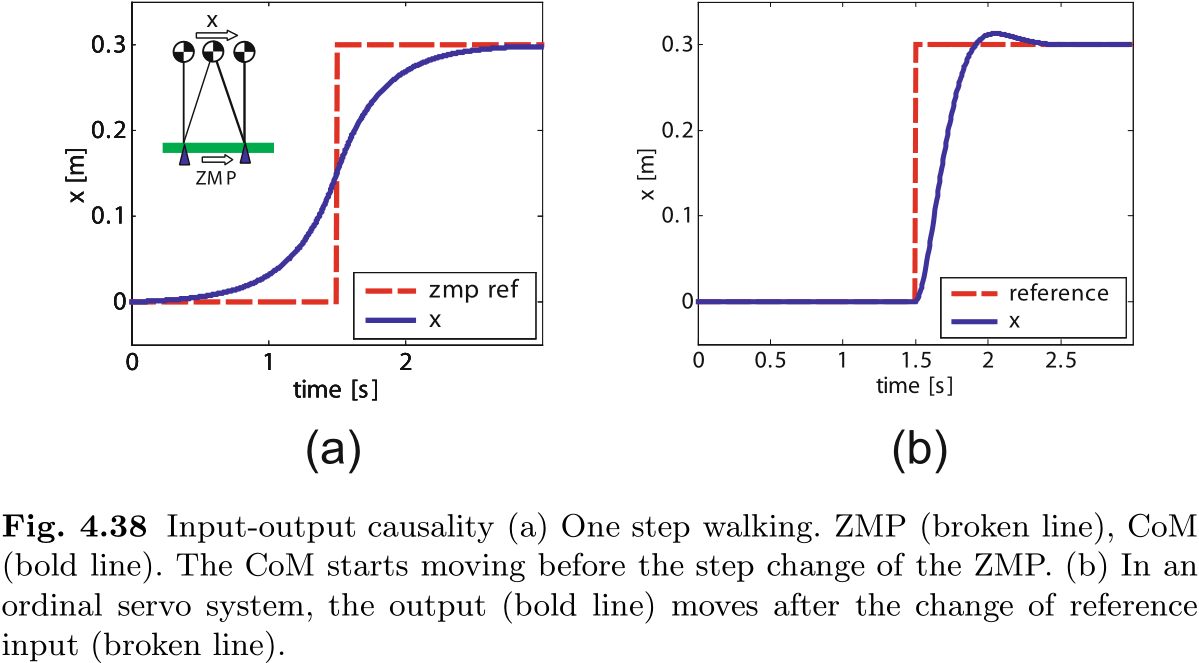
从这个方程出发, 现代控制理论为我们提供了设计控制器的系统方法 [55]. 但是, 我们无法通过这种控制器获得合适的行走模式. 举例来说, 假设图 4.38(a) 中的行走动作要求机器人向前行走 30 厘米. 目标 ZMP 在 1.5 秒时发生阶梯状变化, 但前后保持不变. 请注意, CoM 运动开始于 ZMP 变化之前. 这意味着在图 4.37 的系统中, 小车必须在输入变化之前移动. 另一方面, 在普通伺服系统中, 如图 4.37(b) 所示, 参考点变化后输出运动会有一定的延迟, 这就是正常的因果关系. 在双足行走模式生成过程中, 未来的信息必须回到过去并对过去产生影响！

② 预览控制系统

虽然我们需要未来的信息, 但我们不必开发时间机器. 例如, 在驾驶汽车时, 我们总是在监控前方的道路, 并利用有关汽车未来位置的信息进行转向. 这可以说是利用未来信息实现平稳驾驶. 为了理解使用这些未来信息的重要性, 请想象一下在高速公路上高速行驶时, 挡风玻璃的上半部分被遮挡住, 只能看到前方几米远的地方.

顺便提一下, James P. Hogans的《Thrice upon a Time》 (Baen Books) 中描绘了一种逼真的时间机器技术, 可以利用粒子物理学向过去发送信息. 这是一部科幻小说杰作.

利用未来信息的方法被称为预览控制 [128, 82, 86, 130]. 让我们介绍一种基于该理论的控制器设计.

首先, 我们用 的采样时间对 (4.71) 的连续时间系统进行离散化, 从而设计出一个数字控制器

$$\left\{\begin{align*} &\boldsymbol{x}_{k+1}=\boldsymbol{A}\boldsymbol{x}_k+\boldsymbol{b}_{u_k}\\ &p_k=\boldsymbol{c}\boldsymbol{x}_k \end{align*}\right.\tag{4.72}$$

其中

$$\begin{align*} \boldsymbol{x}_k&\equiv[x(k\Delta t)\enspace\dot{x}(k\Delta t)\enspace\ddot{x}(k\Delta t)]^T,\\ u_k&\equiv u(k\Delta t),\\ p_k&\equiv p(k\Delta t), \end{align*}$$

且

$$\begin{align*} \boldsymbol{A}&\equiv\begin{bmatrix}1&\Delta t&\Delta t^2/2\\0&1&\Delta t\\0&0&1\end{bmatrix},\quad\boldsymbol{b}\equiv\begin{bmatrix}\Delta t^3/6\\ \Delta t^2/2\\ \Delta t\end{bmatrix},\\ \boldsymbol{c}&\equiv[1\enspace0\enspace-z_c/g]. \end{align*}$$

为了让系统输出 尽可能接近目标 ZMP , 我们考虑的问题是使以下性能指标最小化

$$J=\sum_{j=1}^\infty\left[Q(p_j^{ref}-p_j)^2+Ru_j^2\right],\tag{4.73}$$

其中 为正权重. 这就是跟踪控制问题. 根据预览控制理论, 性能指标 可通过以下输入最小化, 该输入使用的是 步以内的未来目标参考[54].

$$u_k=-\boldsymbol{K}x_k+[f_1,f_2,\dots,f_N]\begin{bmatrix}p_{k+1}^{ref}\\ \vdots\\ p_{k+N}^{ref}\end{bmatrix},\tag{4.74}$$

其中

$$\begin{align*} \boldsymbol{K}&\equiv(R+\boldsymbol{b}^T\boldsymbol{P}\boldsymbol{b})^{-1}\boldsymbol{b}^T\boldsymbol{P}\boldsymbol{A},\\ f_i&\equiv(R+\boldsymbol{b}^T\boldsymbol{P}\boldsymbol{b})^{-1}\boldsymbol{b}^T(\boldsymbol{A}-\boldsymbol{b}\boldsymbol{K})^{T*(i-1)}\boldsymbol{c}^TQ. \end{align*}\tag{4.75}$$

矩阵 是以下公式的解

$$\boldsymbol{P}=\boldsymbol{A}^T\boldsymbol{P}\boldsymbol{A}+\boldsymbol{c}^TQ\boldsymbol{c}-\boldsymbol{A}^T\boldsymbol{P}\boldsymbol{b}(R+\boldsymbol{b}^T\boldsymbol{P}\boldsymbol{b})^{-1}\boldsymbol{b}^T\boldsymbol{P}\boldsymbol{A}\tag{4.76}$$

这就是所谓的 Riccati 方程.

您不必担心这个复杂的矩阵方程. 只要使用 Matlab 控制系统工具箱或 GNU Octave 的 dlqr 命令, 就能立即得到 和 的数值解.

通过观察 (4.74), 我们可以发现, 预览控制器由状态反馈 (右侧第一项) 和未来 步目标参考值与权重 之间的内积前馈 (第二项) 组成.

③ 改进预览控制器

我们观察到, 在由 (4.74) 生成的长距离行走模式中, ZMP 存在偏移跟踪误差. 为了解决这个问题, 我们将 (4.72) 改写成以下扩展形式:

$$\left\{\begin{align*} &\boldsymbol{x}_{k+1}^*=\tilde{\boldsymbol{A}}\boldsymbol{x}_k^*+\tilde{\boldsymbol{b}}\Delta_{u_k}\\ &p_k=\tilde{\boldsymbol{c}}\boldsymbol{x}_k^* \end{align*}\right.\tag{4.77}$$

其中, 新的输入和状态向量取为

$$\begin{align*} \Delta u_k &\equiv u_k-u_{k-1},\quad\Delta\boldsymbol{x}_k\equiv\boldsymbol{x}_k-\boldsymbol{x}_{k-1},\\ \boldsymbol{x}_k^* &\equiv\begin{bmatrix}p_k\\ \Delta\boldsymbol{x}_k\end{bmatrix}. \end{align*}$$

矩阵为

$$\begin{align*} \tilde{\boldsymbol{A}} &\equiv \begin{bmatrix}1&\boldsymbol{c}\boldsymbol{A}\\ \boldsymbol{0}&\boldsymbol{A}\end{bmatrix},\quad\tilde{\boldsymbol{b}}\equiv\begin{bmatrix}\boldsymbol{c}\boldsymbol{b}\\ \boldsymbol{b}\end{bmatrix},\\ \tilde{\boldsymbol{c}} &\equiv\begin{bmatrix}1&0&0&0\end{bmatrix}. \end{align*}$$

让我们为 (4.77) 系统设计一个控制器, 以最小化以下性能指标

$$J=\sum_{j=k}^\infty\left[Q(p_j^{ref}-p_j)^2+R\Delta u_j^2\right].\tag{4.78}$$

预览控制器为

$$\Delta u_k=-\tilde{\boldsymbol{K}}\boldsymbol{x}_k^*+\sum_{j=1}^N\tilde{f}_jp_{k+j}^{ref}\tag{4.79}$$

其中, 是将 和 代入 (4.75) 和 (4.76) 得到的增益. 通过对 , 我们就可以得到 (4.72) 原系统的预览控制器:

$$\begin{align*} u_k=-K_s\sum_{i=0}^k(p_j^{ref}-p_j)-K_x\boldsymbol{x}_k+\sum_{j=1}^Ng_jp_{k+j}^{ref}\\ \begin{bmatrix}K_s\\ \boldsymbol{K}_x\end{bmatrix}\equiv\tilde{\boldsymbol{K}},\quad g_j:=\sum_{i=j}^{N+j}\tilde{f}_i. \end{align*}\tag{4.80}$$

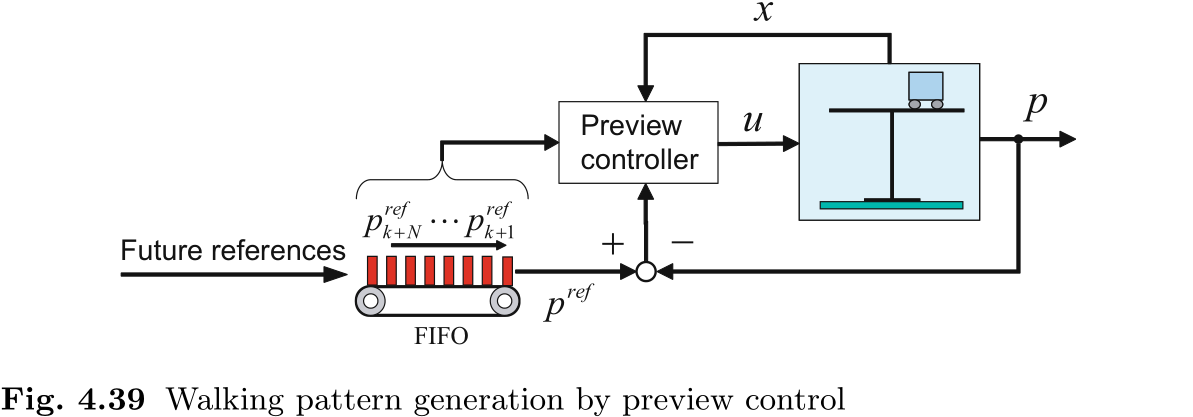
基于预览控制的模式生成框图如图 4.39 所示. 未来的目标 ZMP 参考值存储在一个 FIFO (先进先出) 缓冲器中, 可视化为传送带, 其输出值被视为当前参考值. 预览控制器利用先进先出缓冲器上的 ZMP 参考值和小车状态计算控制输入. 小车状态 是模式生成的结果, 即满足目标 ZMP 的 CoM 运动.

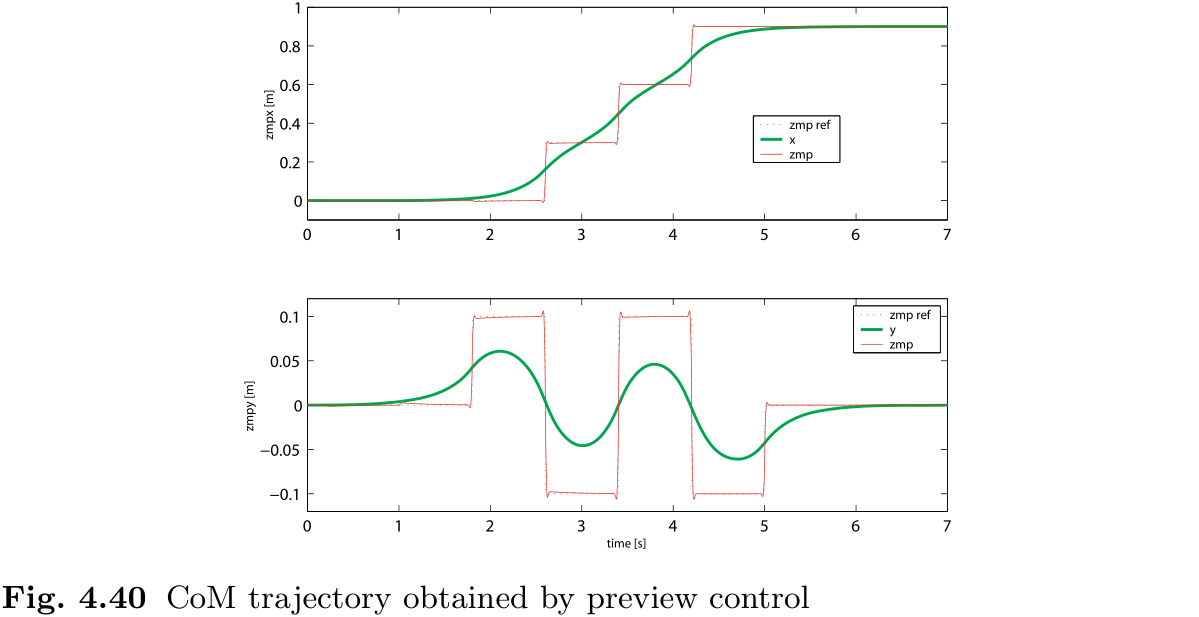
图 4.40 所示为利用所提方法计算出的 CoM 运动轨迹和生成的 ZMP. 上图为沿行走方向的运动轨迹, 下图为横向运动轨迹, 我们可以看到分别为步态目标 ZMP 和脉冲态目标 ZMP 生成了合适的 CoM 运动轨迹. 计算中使用的预览增益如图 4.41 所示. 由于该图中预览增益在 1.6 秒时变得很小, 可以忽略不计, 因此我们可以得出结论, 超过 1.6 秒的未来信息不会对控制性能产生任何影响.

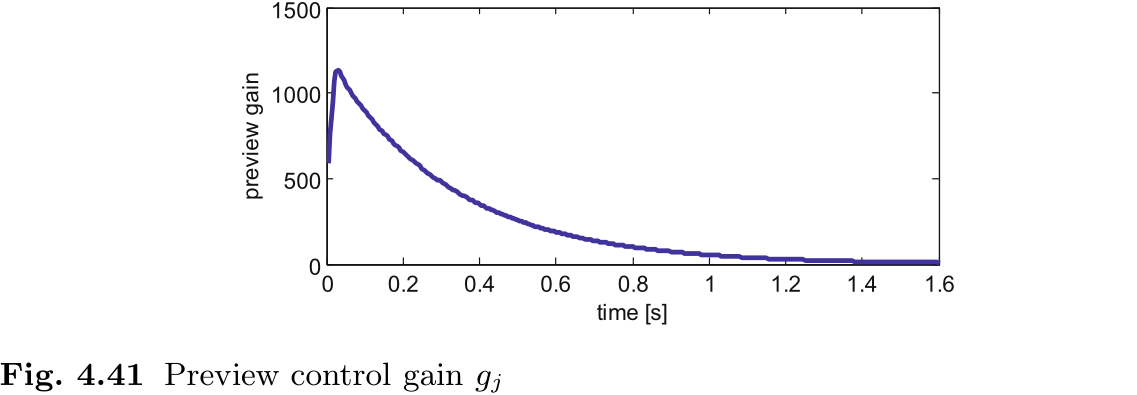
图 4.42 显示了使用上述方法在螺旋楼梯上的行走模式.

4.4.4 基于预览控制的动力学滤波器

① 动力学滤波器的结构

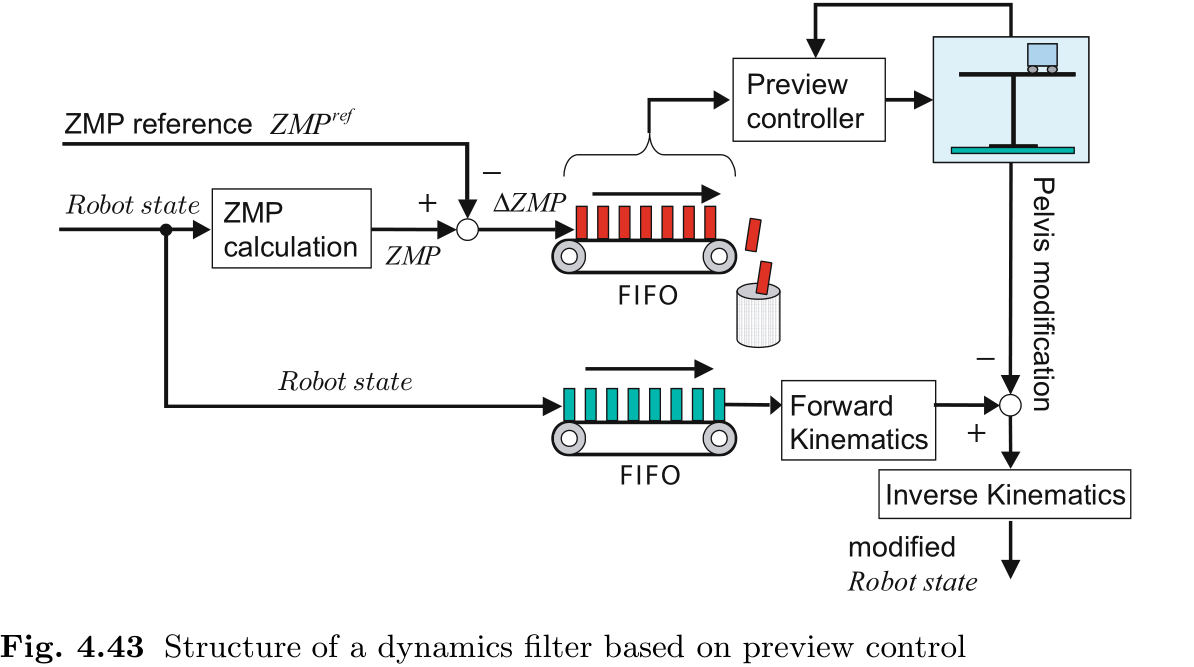
由于基于预览控制的模式生成依赖于推车表模型, 因此无法保证简化模型无法表示的运动的稳定性, 例如, 行走时上半身姿势的显著变化. 不过, 在这种情况下, 我们可以使用 cart-table 模型作为目标运动周围的误差系统, 并通过再次使用预览控制来计算对 CoM 轨迹的修改, 以补偿 ZMP 误差.

图 4.43 显示了系统的整个结构. 输入是目标 ZMP () 和机器人的整个状态 Robot state, 其中包括所有关节的角度和速度, 骨盆参数, 速度和角速度. 我们可以根据这些输入计算 ZMP 误差 (ZMP) , 并将其放入 FIFO 缓冲区. 同时将机器人状态放入另一个 FIFO. 经过一定的时间延迟后, 从 FIFO 输出端读取 ZMP, 我们就可以在 FIFO 缓冲器上得到相对于延迟时刻的未来 ZMP 误差. 因此, 我们可以通过预览控制计算出适当的 CoM 补偿. 通过对延迟的机器人状态进行 CoM 补偿, 我们可以获得改进的关节轨迹, 从而更好地满足目标 ZMP 参考值. 一般来说, 图 4.43 中的系统称为动力学滤波器. 动力学滤波器可将给定的运动模式转换为满足所需特性的改进运动模式 [93].

② 动力学滤波器的评估

举例来说, 让我们制作一个模式, HRP-2 在行走过程中做一个下蹲动作, 之后恢复正常行走, 如图 4.44 所示. 首先, 我们在假定 CoM 高度不变的行走模式中添加一个下蹲动作, 得到的 ZMP 轨迹如图 4.45(a) 所示. 可以看到, ZMP (粗线) 接近支撑多边形 (虚线) 的边界, 行走模式的稳定余量非常小. 因此, 在动力学模拟中, 机器人在下蹲运动后会立即倒下.

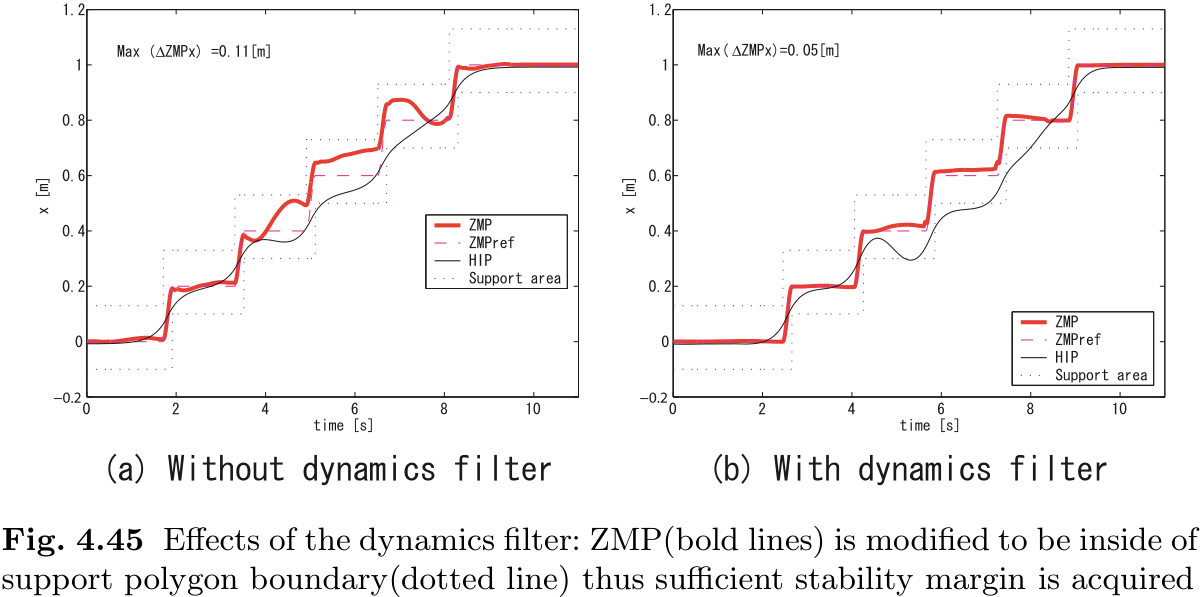
通过图 4.43 中的动力学滤波器对行走模式进行修改, 我们得到了图 4.45(b) 的模式. 我们使用了延迟时间为 0.8 秒的先进先出缓冲器和不带积分器的预览控制器 (见 (4.74)) . 采用动力学滤波器后, ZMP 的最大绝对误差由原来的 0.11 米降至 0.05 米. 由于新的行走模式具有足够的稳定性余量, 机器人可以在动力学模拟中成功行走.

修改后的行走模式如图 4.44 所示. 通过应用所提出的动力学滤波器, 我们可以得到一个可实现的行走模式, 尽管原始模式在很大程度上偏离了简单的 cart-table 模型动力学.

4.4.5 高级模式生成器

预览控制法并不是在线生成行走模式的唯一方法. 作为实用方法之一, Harada 等人提出使用 ZMP 方程的解析解 [60]. 后来, Morisawa 等人对其进行了改进, 使模式生成更高效, 反应更灵敏 [85]. 这些方法被用于实现 HRP-2 的反应式行走.

预览控制属于模型预测控制 (MPC) 的一般方案, 它通过优化未来轨迹来计算控制输入. 基于 MPC, Wieber 提出了一种无需规定 ZMP 的行走模式生成方法 [137,9]. 通过这种方法, 可以根据给定的支撑多边形轮廓同时生成 ZMP 和 CoM 轨迹.

4.5 稳定器

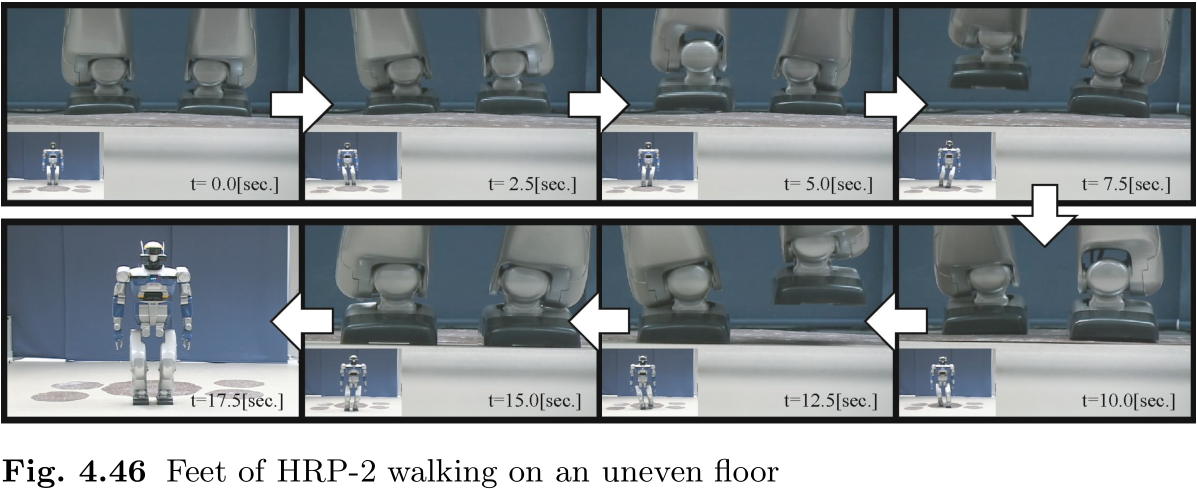
图 4.46 显示了 HRP-2 在不平地面上行走的快照. 正如本章开头所解释的那样, 在包含未建模误差和地面不平的真实环境中, 双足机器人按照事先准备好的模式行走时, 参考状态和实际状态之间的误差会迅速演变, 并在几步之内摔倒. 为了抑制误差的发展, 并保证沿着指定的行走模式行走, 我们使用了稳定器.

4.5.1 稳定控制原理

在本节中, 我们将介绍用于构建稳定器的基本原理. 为了简化说明, 我们将解释一种围绕静止状态进行稳定的方法. 由于稳定器的作用是吸收参考行走模式周围的微小误差, 因此我们不应该因为这种方法而失去一般性.

① 踝关节力矩控制

我们可以通过将整个机器人建模为一个简单的倒立摆, 利用支撑腿的踝关节力矩来稳定整个身体的平衡或姿势.
踝关节力矩 与线性倒立摆的关系为

$$\ddot{x}=\frac{g}{z_c}x+\frac{1}{Mz_c}\tau.\tag{4.81}$$

稳定该摆的最简单反馈定律如下:

$$\tau=-k_px-k_d\dot{x},\tag{4.82}$$

其中, 是针对给定响应频率 和阻尼系数 确定的反馈增益

$$k_p\equiv M(z_c\omega_n^2+g),\quad k_d\equiv2Mz_c\zeta\omega_n.$$

虽然这一控制法则看起来很简单, 但实施起来却很困难. 首先, 对于大多数配备高减速齿轮的行走机器人来说, 脚踝力矩的精确控制是一个极其困难的问题. 此外, 为了实现稳定行走, 我们需要对反馈增益和力矩限制器进行微调, 以抑制因脚踝力矩过大而导致的脚趾/脚跟抬起.

20 世纪 80 年代和 90 年代开发的许多双足机器人都采用了这种方法, 例如 Takanishi 等人的 WL-10RD 机器人[10], Miyazaki 和 Arimoto 的 Idaten II 机器人[109, 32], Sano 和 Furuhso 的 Kenkyaku-2 机器人[46] 以及 Kajita 和 Tani 的 Meltran II 机器人[116].

② 通过调整脚的位置进行控制

基于倒立摆模型的第二种方法是修改脚的位置以实现稳定. 对于这种控制, 我们可以采用与第 4.3.3 节中解释的行走速度控制相同的原理 (见第 129 页图 4.23) . 通过修改脚的位置来实现稳定的机器人不在少数, 例如 Shimoyama 和 Miura 开发的高跷步行器 BIPER-3 [41], 以及 Raibert 和他的同事开发的一系列跳跃机器人 [97].

③ 通过 CoM 加速实现 ZMP 控制

让我们考虑一下基于 cart-table 模型的稳定方法. 在这种情况下, 我们必须测量 ZMP 来设计反馈控制器, 假设 ZMP 传感器的时间常数为 , 则 ZMP 方程为

$$p=\frac{1}{1+sT}\left(x-\frac{z_c}{g}\ddot{x}\right).\tag{4.83}$$

以小车加速度 为输入的状态空间表示为

$$\frac{d}{dt}\begin{bmatrix} p\\x\\ \dot{x} \end{bmatrix}=\begin{bmatrix} -1/T&1/T&0\\0&0&1\\0&0&0 \end{bmatrix}\begin{bmatrix} p\\x\\ \dot{x} \end{bmatrix}+\begin{bmatrix} -z_c/(gT)\\0\\1 \end{bmatrix}\ddot{x}.\tag{4.84}$$

我们可以设计一个状态反馈定律来稳定这个系统, 即

$$\ddot{x}=-k_1p-k_2x-k_3\dot{x}.\tag{4.85}$$

反馈增益 可通过极点放置或 LQ 最佳控制等标准控制理论确定. Nagasaka, Inaba 和 Inoue [70] 将此控制法则作为*躯干位置顺应控制引入. 该控制法则对具有高刚度脚的行走机器人非常有效, 并被用于稳定仿人机器人 H5 和 H7[113]. Choi, Kim 和 You [139] 提出了一种更简单但有效的控制器.

*在最初的工作中, 他们使用了不同的程序来推导等效控制律. Napoleon 等人根据零动力控制理论对他们的控制法则进行了另一种解释 [94].

作为一种替代方法, Okada, Furuta 和 Tomiyama 提出了一种通过动态改变采样时间来控制 CoM 加速度的稳定方法, 并用于控制双足机器人 MK.3 和仿人机器人 morph3 [143].

④ 通过胯部关节控制身体姿势

对于大多数行走机器人来说, 我们希望在行走过程中身体保持直立姿势. 最简单的方法是旋转胯部 (臀部) 关节, 使身体根据姿势传感器的读数保持所需的状态. 即使是点接触脚也能做到这一点, 因为胯关节周围的力矩是由地面摩擦力产生的. 这种控制在 Raibert 的跳跃机器人 [97] 和 Kumagai 等人开发的仿人机器人 [84] 中得以实现.

⑤ 模型 ZMP 控制

作为一种新颖的身体姿态控制方法, Hirose, Takenaka 等人提出了一种 ZMP 控制模型. 根据他们的解释, 其工作原理为

当真实机器人的身体比模型更向前倾斜时, 模型身体的加速度比计划轨迹更大. 这就改变了目标惯性力, 目标 ZMP 就会比原来的 ZMP 更加向后, 从而使真实机器人产生姿态恢复[83, 62].

让我们使用图 4.47 中的 cart-table 模型来考虑这种模型 ZMP 控制的物理意义. 我们假设台脚有一个可自由旋转的关节, 可使台面相对于垂直位置倾斜 角. 推车加速度 相当于车身加速度.

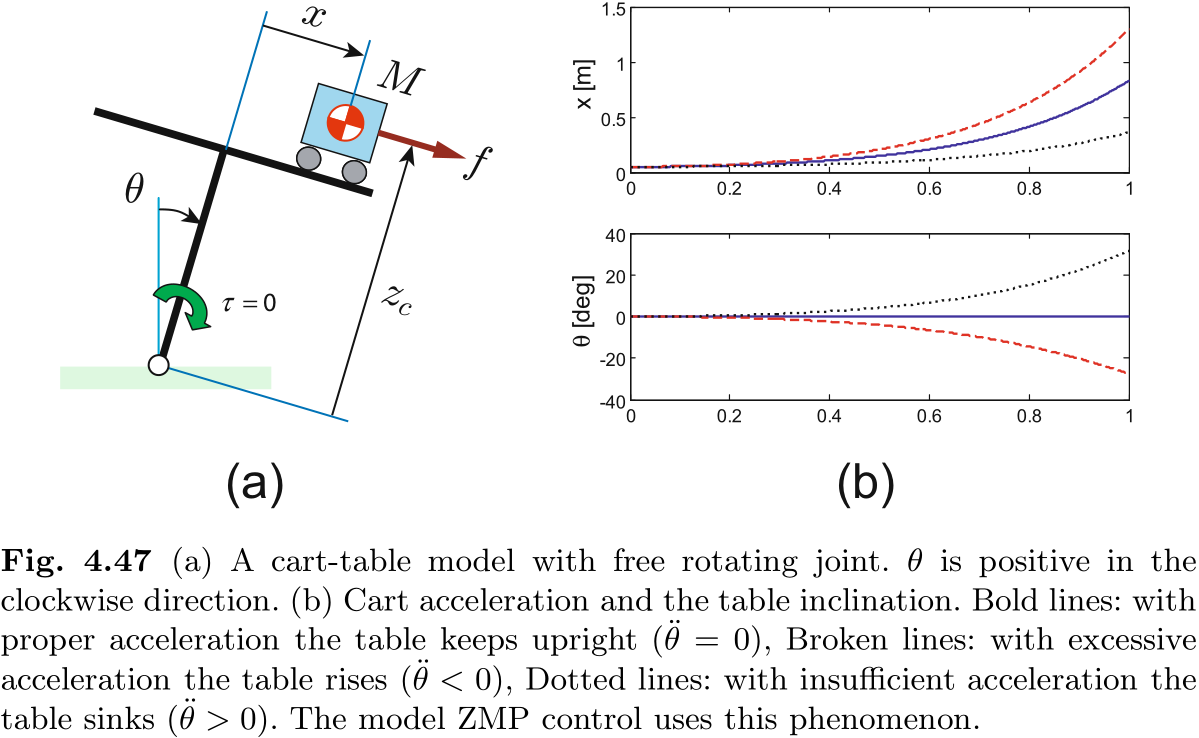
用拉格朗日方法得到的运动方程为

$$\left\{\begin{align*} &(x^2+z_c^2)\ddot{\theta}+\ddot{x}z_c-g(z_c\sin\theta+x\cos\theta)+2x\dot{x}\dot{\theta}=\tau/M\\ &\ddot{x}+\ddot{z}_c-\dot{\theta}^2x+g\sin\theta=f/M \end{align*}\right.\tag{4.86}$$

其中, 是作用于桌脚的力矩, 是小车在桌面上的加速力. 将第一个方程绕 线性化, 即 , 并代入 , 可得

$$(x^2+z_c^2)\ddot{\theta}=gx+gz_c\theta-z_c\ddot{x}.\tag{4.87}$$

接下来, 假设小车的目标位置 是由以下动力学参数生成的

$$\ddot{x}_d=\frac{g}{z_c}(x_d-p_d),\tag{4.88}$$

其中 为目标 ZMP. 直观地说, 当目标 ZMP 置于后方 () 时, 小车加速度大; 当目标 ZMP 置于前方 () 时, 小车加速度小. 由于 (4.88) 只是一个产生加速度的模型, 因此可以将目标 ZMP 指定在支撑多边形的外侧.

现在, 假设我们可以随心所欲地控制小车的加速度. 将 和 (4.88) 代入 (4.87) 即可得到

$$\ddot{\theta}=\frac{gz_c}{x_d^2+z_c^2}\theta+\frac{g}{x_d^2+z_c^2}p_d.\tag{4.89}$$

从这一结果可以看出, 工作台倾斜度 可由目标 ZMP 控制, 其动态变化由小车位置和重力加速度决定.

⑥ 关节反向驱动的冲击吸收

通过嵌入关节力矩传感器并将参考位置作为力矩测量的函数, 我们可以实现一个虚拟弹簧减震系统. Takanishi 等人利用这种系统吸收了触地冲击时的振动 [10]. 此外, 当一个关节的减速比很小时 (约为 1/1 至 1/50) , 它就会受到来自环境的外力的反向驱动, 因此位置控制系统本身就像一个弹簧阻尼器. Furusho 等人开发的双足机器人 Kenkyaku 1 就是利用这种方式进行行走控制的[47]. Sorao, Murakami 和 Ohnishi 提出了利用阻抗控制器在支撑物交换时吸收冲击力的方法, 该方法依赖于干扰观测器的无传感器力矩测量[75].

⑦ 通过 LQ 控制实现稳定

行走机器人可以建模为一个多输入多输出 (MIMO) 系统, 其输入向量为关节力矩 , 输出为所有链节的状态. 让我们定义一个由所有链节的姿态和速度变量组成的状态向量 , 并将 到 的运动方程线性化. 通过直接应用 LQ 控制理论, 我们可以得到以下状态反馈定律

$$\boldsymbol{u}=-\boldsymbol{K}\boldsymbol{x},$$

其中 是反馈增益, 对于关节数 而言是一个巨大的 矩阵. Mita 等人[133] 将这种方法应用于 6 DOF 双足机器人 CW-2 和 Yoshino [145] 开发的 12 DOF 双足机器人. 特别是后者的研究报告指出, 机器人可以成功地以 3 [km] 的速度行走.

4.5.2 本田仿人机器人的稳定控制

结合上述多种控制原理, 就能构建出实用的稳定控制系统. 让我们回顾一下这样一个成功的实施方案.

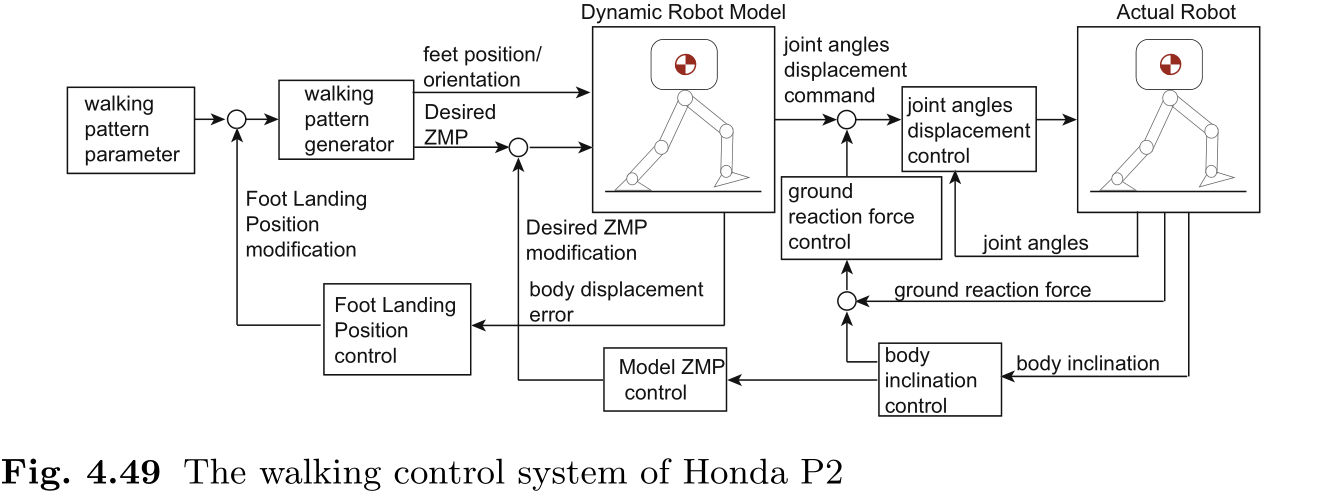
图 4.48 是本田汽车有限公司开发的仿人机器人 P2, 于 1996 年正式发布. 其控制系统即使在印刷时也已达到最先进的水平, 其技术也已被充分披露 [83, 62]. P2 的行走控制系统如图 4.49 所示. 从身体倾斜度到地面反作用力的反馈路径与 ① 中描述的踝关节力矩控制相对应. 值得注意的是, P2 脚部插入的被动顺应元件使这一控制更容易实现. 当机器人机身过度倾斜时, 模型 ZMP 控制器 ⑤ 将发挥作用解决这一问题. 由此产生的水平位移误差则由脚着地位置控制 ② 进行修正. 正如我们所看到的, P2 的稳健行走控制由多种控制方案的巧妙组合提供支持.

4.5.3 高级稳定器

最近, 我们提出了一种基于 LIPM 状态空间模型和 ZMP 控制滞后的新型稳定器 [117]. 通过这种稳定器, 我们的新型仿人机器人 HRP-4C 可以在一定程度的不平地面上行走, 还能在脚趾支撑的情况下进行类似人类的行走 [69]. 该稳定器的关键问题之一是适当设置状态反馈增益, Sugihara [125] 对此进行了讨论. 另一个重要问题是所需 ZMP 的分布. Hyon [42] 讨论了基于总地力分布的相关稳定概念.

行走过程中的巨大干扰, 例如踢到身体, 会立即导致机器人偏离预先规划的轨迹, 从而摔倒. 在这种情况下, 如果机器人能将偏离状态作为初始条件, 重新规划行走模式, 就能避免摔倒. 通过正确实施这一概念, 可以实现非常稳健的行走 [72, 85, 51].

正如我们在第 4.5.1 节中所讨论的, 自适应改变脚的位置是实现稳定的基本策略. Pratt 等人定义了捕捉点, 即机器人在地面上迈出一步就能实现完全停止的点[50]. 基于捕捉点概念, Englsberger 等人提出了一个用于实时生成行走模式和稳定的简单框架 [44].

4.6 动态双足行走技术的先驱

让我们回顾一下动态双足行走控制的研究历史. 自机器人研究诞生之初, 双足行走就被公认为是一项难度最高的挑战. 最早的硬件开发研究始于 1966 年早稻田大学的 Ichiro Kato 和 1968 年牛津大学的 D.C. Witt[68, 19]. 正如我们在第 1 章中介绍的那样, 1973 年, Ichiro Kato 和他的同事们制造出了世界上第一个仿人机器人 WABOT-1, 它有两只胳膊和两条腿, 由计算机控制. 虽然这是一项了不起的成就, 但 WABOT-1 只能进行静态行走. 大约在 1980 年, 日本掀起了一股实现动态双足行走的研究热潮, 许多日本研究人员积极开发相关理论和机器人硬件. 我们可以在 [Special Issue: Biped Walking Robot, the journal of Robotics Society of Japan, Vol.1, No.3.] 中看到这些活动. 1986 年, 已经出现了许多可以进行动态行走的双足机器人, 如图 4.50 所示[27].

同年, 本田技研工业株式会社的一组研究人员开始了一项双足行走机器人的秘密项目. 在沉寂了 10 年之后, 他们的努力终于结出了硕果, 人形机器人 P2 诞生了. 人形机器人 P2 以其出色的硬件和行走控制技术突然出现, 让在此之前一直致力于双足行走控制的研究人员感到非常沮丧. 与此同时, 它也激励了许多研究人员, 展示了仿人机器人的巨大可能性. 这为启动日本国家研发项目--仿人机器人项目 (1998-2002 年) 提供了动力.

据估计, 与大学相比, 本田公司在此期间投入的资金和人力是大学的 100 倍以上. 由于当时的机器人界对双足机器人大多持否定态度, 本田人的长远眼光值得尊敬！

看惯了 ASIMO 或 QRIO 的人可能会认为图 4.50 中的机器人很原始. 然而, 那些在当时简陋的计算机和薄弱的致动器条件下开发出这些机器人的研究人员才是双足行走技术的真正先驱. 事实上, 大部分双足行走的建模和控制技术都是在那个时代才开发出来的. 此外, 我很难相信本田的研究项目是独立于 1986 年已经发表的许多研究成果之外的. 科学技术的进步不是一个天才一夜之间就能完成的. 没有独立于遗产之外的辉煌突破. 因此, 真正的进步只能通过许多研究人员的合作, 超越研究所, 超越国家, 进行开放式的思想交流来实现.

4.7 其他双足控制方法

在本节中, 我们将介绍双足机器人和基于完全不同于上述概念的控制方法.

4.7.1 被动式动态行走

被动动态步行器是一种仅利用势能就能在浅坡上行走的装置. Tad McGeer 对其动力学进行了深入分析, 并设计出一种带有自由膝关节的二维步行器, 无需任何驱动或控制, 就能像人一样行走, 令人惊叹[131, 132]. 在这一概念的基础上, Collins, Wisse 和 Ruina 又实现了三维被动行走器[111]. 被动动态行走吸引了许多研究人员, 他们都在寻找双足运动的基本性质. 有研究分析了其混沌行为 [14, 74] 和鲁棒稳定性 [141].

在 McGeer 的原始论文[131]中, 他提出了一种 "动力" 被动式步行器, 通过添加小型致动器, 它可以在平地或上坡时行走. 这就是所谓的半被动动态助行器. 目前已有一些理论著作[7, 29, 91], Hobbelen 和 Wisse [21] 以及 Narioka, Tsugawa 和 Hosoda [71] 等人开发了成功的实施方案. Collins, Ruina, Tedrake 和 Wisse 评估了他们成功研制的半被动式步行器的功耗, 估计其中一个机器人的效率比本田的 ASIMO 高出约十倍[110].

4.7.2 非线性振荡器和中央模式发生器

一些研究人员认为, 双足行走不应该是经过分析规划的, 而必须是系统与环境之间的反馈和动态互动所产生的非线性振荡的结果.

Katoh 和 Mori 制造了一种高跷型双足机器人 BIPMAN2, 该机器人使用基于耦合范德波尔方程的非线性振荡器产生的稳定极限循环. 该机器人可向前迈出一个动态步幅 [100].

Taga 等人利用分布式非线性振荡器 (中央模式发生器: CPG) 模拟了人类的肌生系统, 发现模拟的机器人可以自然地产生行走或奔跑动作, 并对干扰具有鲁棒性 [126].

受 Taga 工作的启发, Hase 等人模拟了由分层 CPG 系统控制的详细三维人体模型, 并演示了稳定的三维行走和跑步[61]. 他们还使用爬山算法来优化 CPG 参数以获得各种性能指标, 并报告说成功获得了具有类人特性的行走模式.

最近, Hyon, Morimoto 和 Kawato 展示了他们的人形机器人基于 CPG 的动态行走 [107].

4.7.3 学习与进化计算

最激进的方法可能是制造一个能够自我学习或进化行走的机器人. Doya 制造了一个简单的双足机器人, 它由三个链节和一个硬件自学习系统组成. 该系统随机生成一种行走模式, 并使用爬山算法进行学习, 该算法以实际行走距离作为性能指标[57]. 结果, 机器人可以获得各种行走模式, 包括跳跃步态和翻滚步态, 这在意料之外. de Garis 设计了一种基于神经网络的行走控制系统, 其权重由遗传算法调整, 并模拟了双足行走的进化过程[20].

Tedrake 等人设计了一种三维半被动式步行器, 配备四个致动器, 其运动可通过在线强化学习获得. 据报道, 该机器人可在大约二十分钟内学会适合各种地面条件的行走模式[106].