本文为书籍 Introduction to Humanoid Robotics 的汉化, 主要借助翻译器 DeepL.
另外, 原书有管贻生教授的译作版本:《仿人机器人》(清华大学出版社, 2007年). 强烈推荐.
3 零力矩点与动力学 (ZMP and Dynamics)
本节的主要内容是机器人的物理学, 而上一章的主要内容是几何学.
我们首先展示了一种测量 ZMP 的方法, ZMP 是仿人机器人的一个重要物理量. 然后, 我们展示了针对仿人机器人的给定运动计算 ZMP 的方法. 最后, 我们解释了关于 ZMP 的某些错误以及无法使用 ZMP 处理的情况.
3.1 ZMP 和地面反作用力
工业机器人的底座固定在地面上, 而仿人机器人的脚底并不固定, 只是与地面接触. 因此, 虽然工业机器人可以在关节活动范围内自由移动, 但仿人机器人却必须在保持脚底与地面接触的困难条件下移动. 在这里, 给定一个仿人机器人的运动, 我们需要判断脚底和地面之间是否能保持接触. 此外, 我们还需要规划一个保持脚底与地面接触的仿人机器人运动. 我们通常使用 ZMP 来实现这些目的.
3.1.1 ZMP 概述
① ZMP 的定义
1972 年, Vukobratović 和 Stepanenko 在关于仿人机器人控制的论文开头定义了零力矩点 (ZMP) . 有关 ZMP 的所有论述都从这里开始.
我们可以在书 [81] 中找到相同的定义. 后来, Vukobratović 和 Borovac [88] 讨论了 ZMP 定义的一些微妙之处.
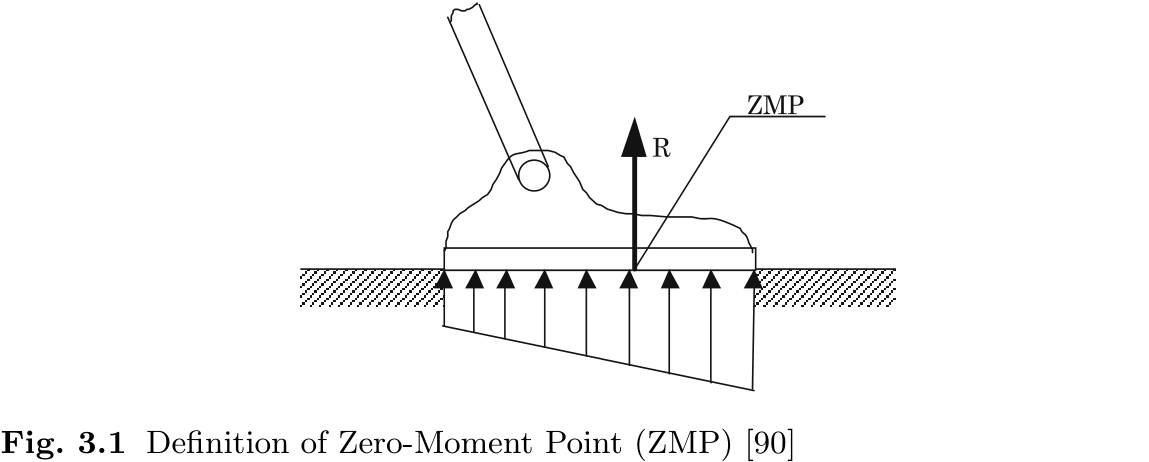
图 3.1 给出了整个脚部的力分布示例. 由于整个表面的载荷符号相同, 因此可以将其简化为合力
② ZMP 和支撑多边形

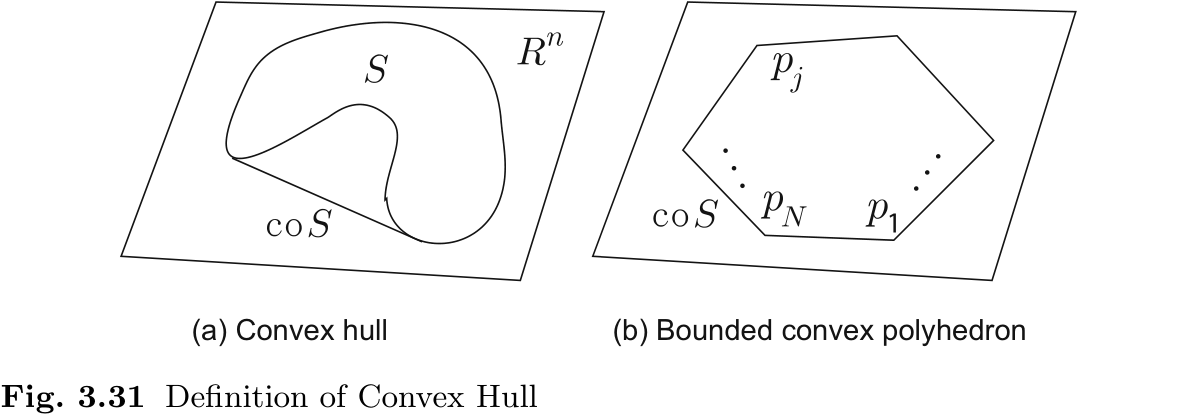
我们将解释与 ZMP 有关的另一个重要概念--支撑多边形. 如图 3.2 所示, 让我们考虑使用弹性绳编织带包围机器人与地面之间所有接触点所形成的区域. 我们称这一区域为支撑多边形. 在数学上, 支撑多边形被定义为一个凸包, 它是包括所有接触点的最小凸集. 本章附录将解释凸集和凸包的定义.
我们不作详细讨论, 而是首先说明 ZMP 与支撑多边形之间简单而重要的关系, 即
✨ ZMP 始终存在于支撑多边形内.
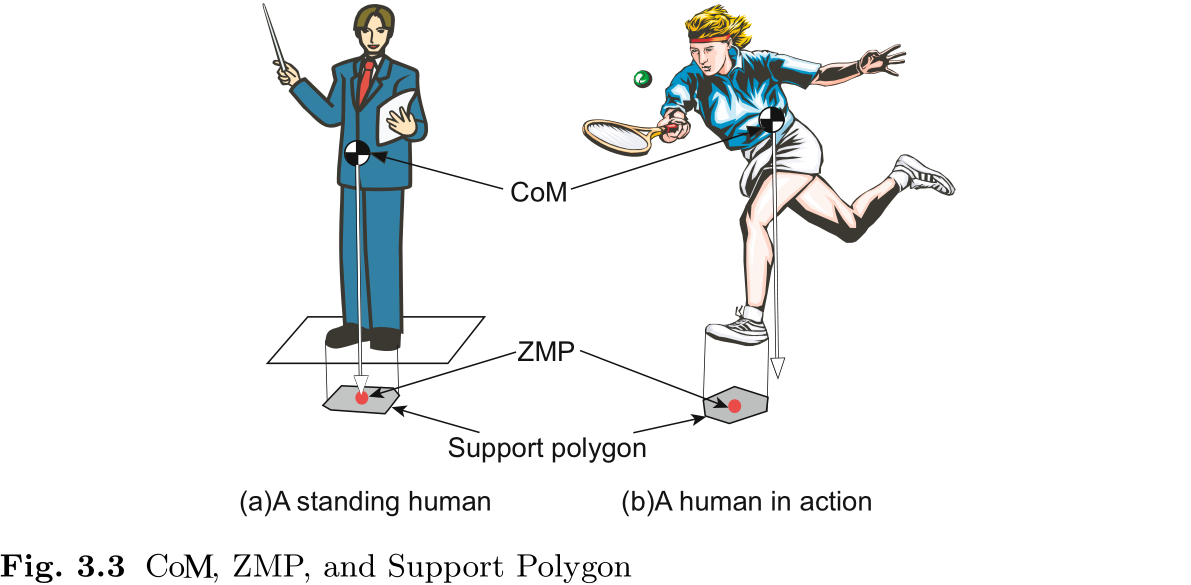
这里, Vukobratović 最初的说法是 "存在于脚的边界内的点". 为了更具体地说明这一点, 请看图 3.3, 图中说明了人站在地面上时质心 (CoM) , ZMP 和支撑多边形之间的关系. 我们将 CoM 的地面投影称为 CoM 的重力线与地面的交点. 如图 3.3(a) 所示, 当人站在地面上时, ZMP 与 CoM 的地面投影重合. 在这种情况下, 如果 CoM 的地面投影严格位于支撑多边形的内部, 人就能保持平衡. 另一方面, 当人如图 3.3(b) 所示动态移动时, CoM 的地面投影可能存在于支撑多边形之外. 但是, ZMP 从不存在于支撑多边形之外. 下面我们将解释 ZMP 始终包含在支撑多边形中的原因.
3.1.2 2D 分析
① 2D 中的 ZMP
在图 3.1 中, 虽然只显示了地面反作用力的垂直分量, 但由于地面和脚底之间的摩擦力, 地面反作用力的水平分量也是存在的.
在图 3.4(a) 和 (b) 中, 我们分别显示了鞋底单位长度上地面反作用力的垂直分量
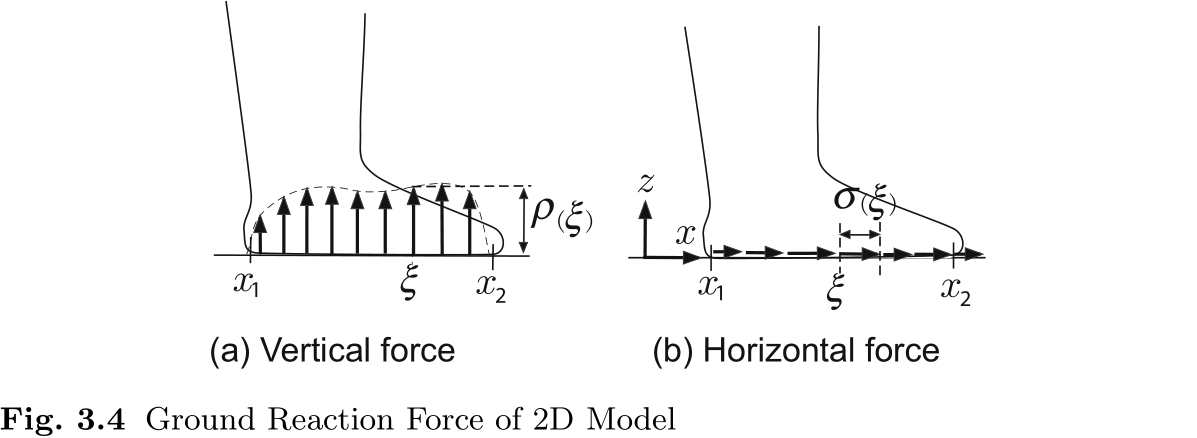
让我们用鞋底某一点上的等效应力和力矩来代替分布在鞋底上的力. 鞋底
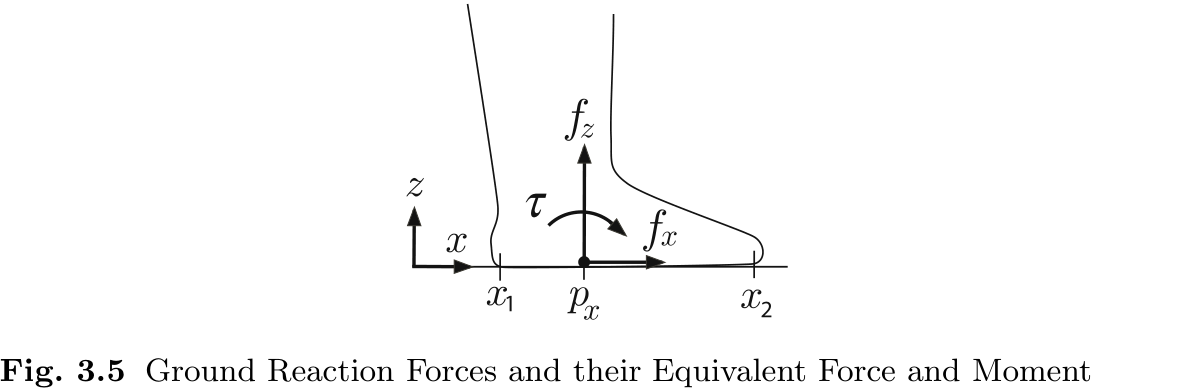
针对 (3.3) 中的力矩, 让我们考虑力矩变为零的点
这里,
② 2D 中的 ZMP 区域
一般来说, 除非在鞋底安装磁铁或吸盘, 否则地面反作用力的垂直分量不会变为负值,
将这一关系代入 (3.4), 我们得到
公式 (3.5) 意味着 ZMP 包含在鞋底与地面的接触区域中, 而不存在于接触区域之外.
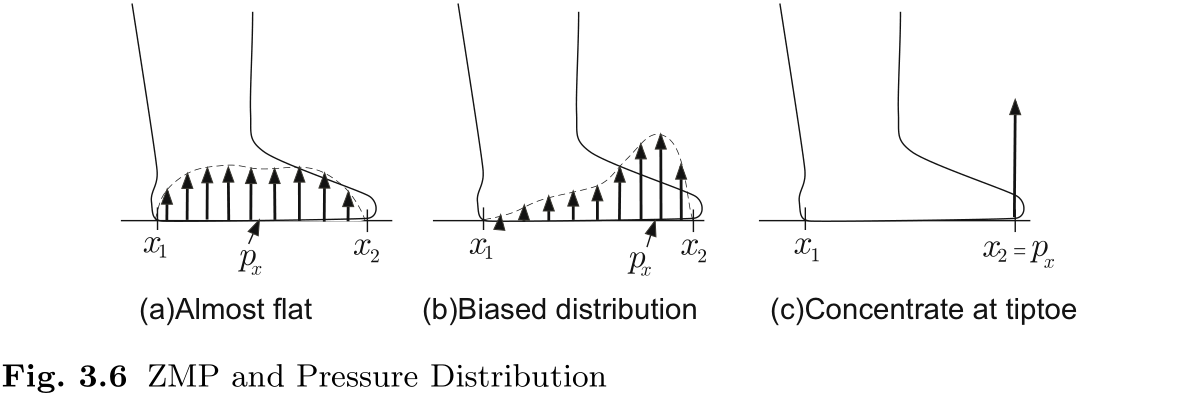
图 3.6 显示了压力分布与 ZMP 位置之间的关系. 如 (a) 所示, 当反作用力几乎平均分布于鞋底时, ZMP 存在于鞋底中心. 另一方面, 如 (b) 所示, 当压力分布向鞋底前部倾斜时, ZMP 存在于鞋底前部. 此外, 如图 (c) 所示, 当脚趾处的一个点支撑所有反作用力时, ZMP 也存在于脚趾处. 在这种情况下, 由于鞋底与地面之间的表面接触不再得到保证, 因此只需对机器人施加轻微的外部干扰, 脚就会开始围绕脚趾旋转. 为了减少仿人机器人移动时摔倒的危险, 最好让 ZMP 位于支撑多边形内部, 同时与边缘保持一定的距离.
3.1.3 3D 分析
现在, 我们将 ZMP 的概念扩展到三维情况.
① 3D 中的地面反作用力
让我们来看看机器人在三维空间中从平地移动时所受到的地面反作用力. 地面反作用力的水平分量和垂直分量分别如图 3.7(a) 和 (b) 所示. 在实际情况中, 这两个分量的总和会同时作用在机器人身上.
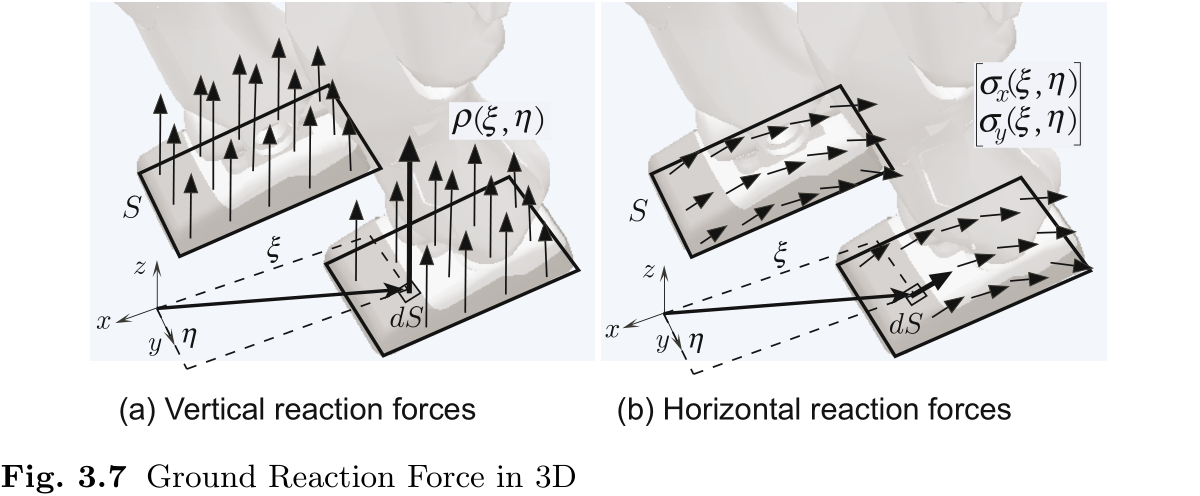
设
其中,
与二维情况一样, 假设
对于 (3.8) 和 (3.9), 地面反力垂直分量的力矩变为零的点可表示为
由于
另一方面, 让我们考虑地面反作用力水平分量的影响. 设
水平地面反作用力对地表某点
这些公式意味着水平地面反作用力产生了力矩的垂直分量.
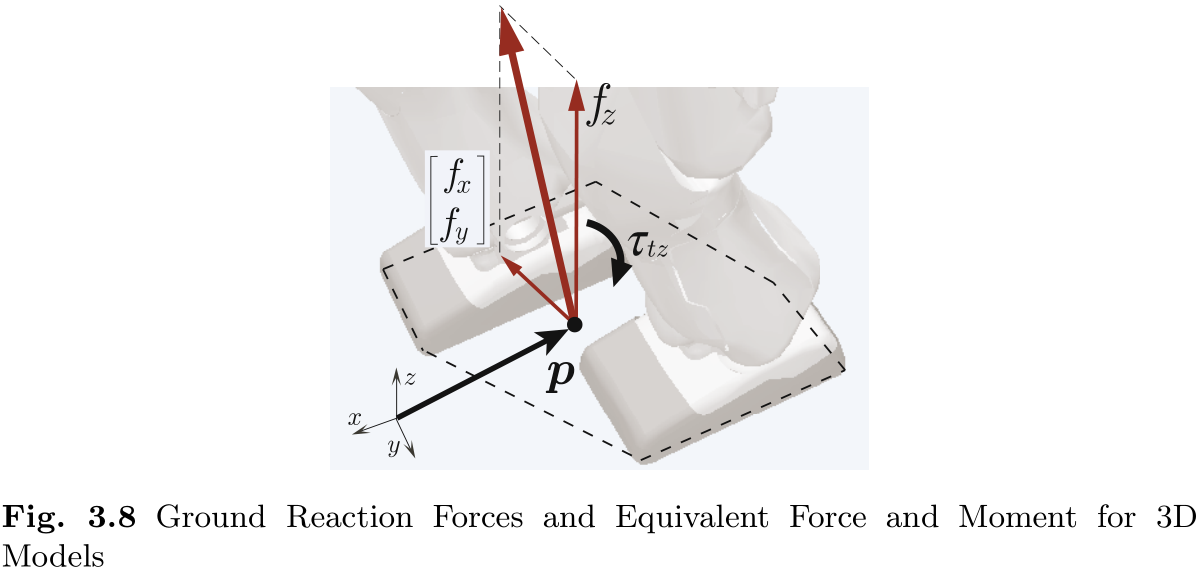
从上面的讨论中我们可以看出, 如图 3.8 所示, 分布在鞋底表面的地面反作用力可以用以下力来代替
以及关于 ZMP 点
当机器人移动时,
② 3D 中的 ZMP 区域
让我们定义三维情况下的 ZMP 区域. 为简单起见, 我们考虑作用于离散点
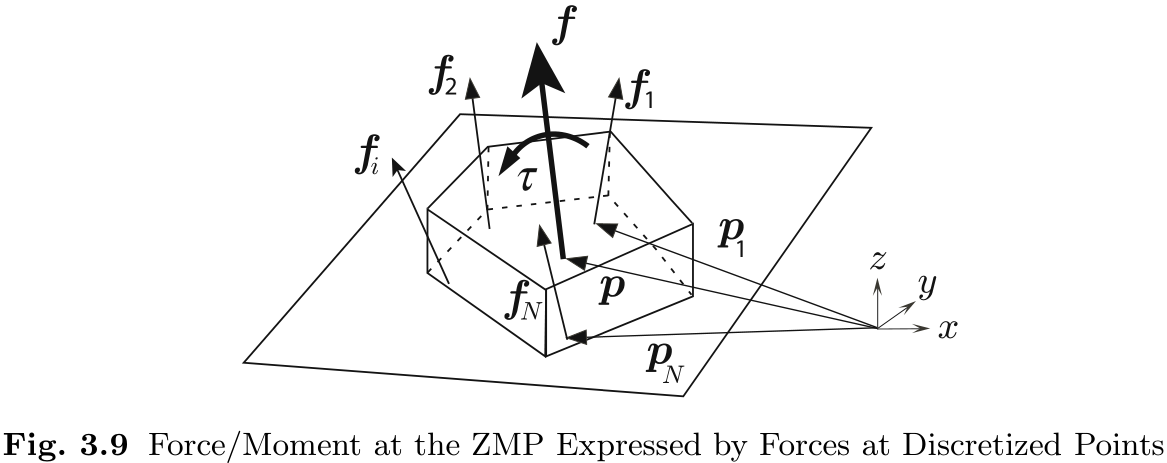
接下来, 分散的
将 (3.18) 中的第一个和第二个元素设为零, 就可以得到 ZMP 的位置. 由此得出
对于底部没有磁铁或吸盘的普通仿人机器人, 地面反作用力的垂直分量在所有离散点上都为零, 即
这里引入新变量
通过使用
将 (3.21) 和 (3.22) 与第 3.6 节中凸包的定义 (3.90) 进行比较, 我们可以发现 ZMP 包含在集合
3.2 测量 ZMP
本节将介绍使用连接在仿人机器人脚部的多个传感器测量 ZMP 位置的方法. 对于双足行走机器人来说, 要测量 ZMP 的位置, 我们应该考虑两种情况, 即: (1) 每只脚的 ZMP, 考虑其中一只脚与地面之间的反作用力; (2) ZMP 考虑两只脚与地面之间的反作用力. 在双支撑阶段, 这两个 ZMP 会发生变化.
3.2.1 一般性讨论
让我们来看看图 3.10 所示的模型. 在这个模型中, 有两个刚体相互接触, 其中一个刚体还与地面接触. 一个刚体对另一个刚体施加的力和力矩是在多个点测量的. 该模型模拟仿人机器人的脚. 当机器人移动, 脚部受力于地面时, 脚部的力/力矩传感器就会产生输出. 利用这些传感器信息, 可以测量 ZMP 的位置.
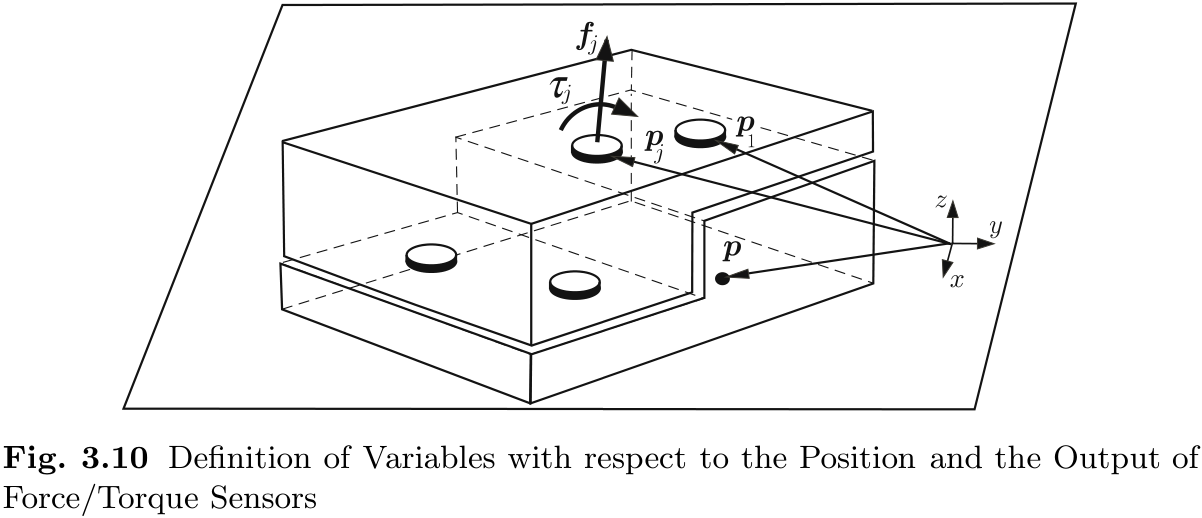
假设在
将 (3.23) 的
其中
方程 (3.24) 和 (3.25) 是测量 ZMP 位置的基础.
当脚不接触地面时, 由于 (3.24) 和 (3.25) 的分母为零, 因此无法确定 ZMP 位置. 因此, 在测量 ZMP 时, 我们必须引入一个阈值, 当分母小于阈值时, 设置
.
3.2.2 每只脚的 ZMP
首先, 我们以单脚与地面的接触为重点, 测量 ZMP.
① 使用 6 轴力/力矩传感器进行测量
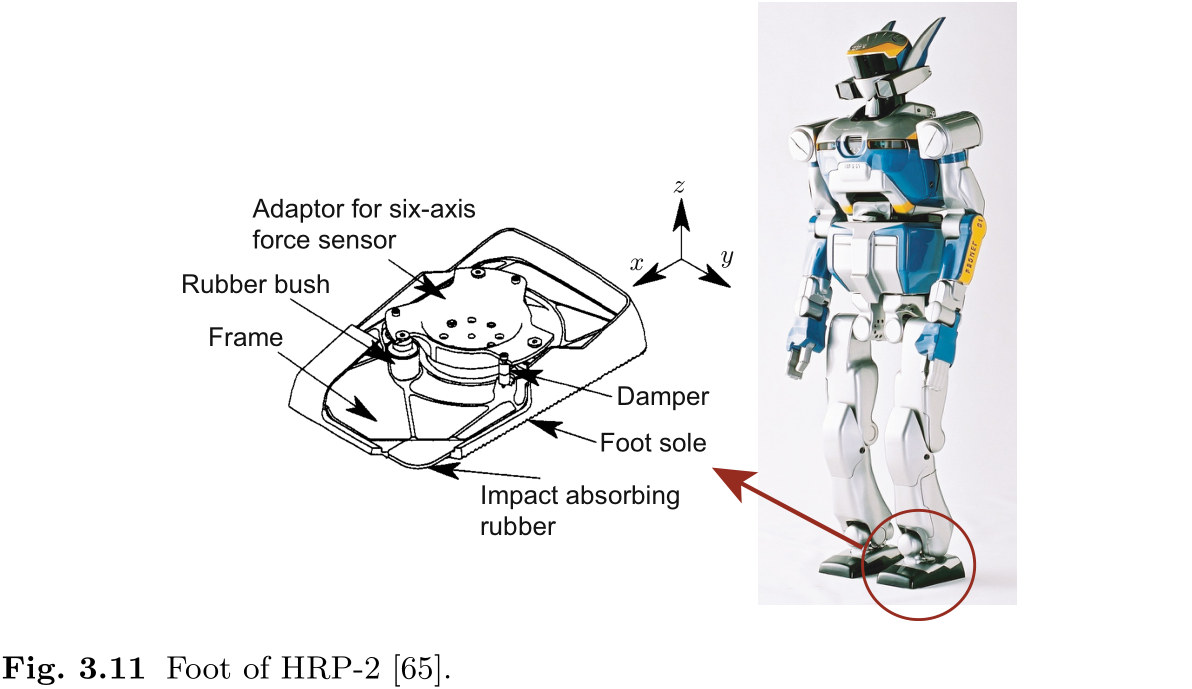
图 3.11 显示了仿人机器人 HRP-2 的脚[65]. 施加在脚底的地面反作用力通过橡胶衬套和阻尼器传递到传感器支架. 传感器支架上安装有一个 6 轴力/力矩传感器, 力通过该传感器传递到机器人的脚踝. 橡胶衬套和阻尼器的设置是为了防止较大的冲击力传递给机器人. 由于它们的位移很小, 我们在计算 ZMP 时不考虑位移.
6 轴力/力矩传感器可同时测量从机器人外部施加的力
从 6 轴力/扭矩传感器的测量数据中获取 ZMP, 我们在 (3.24) 和 (3.25) 中设置

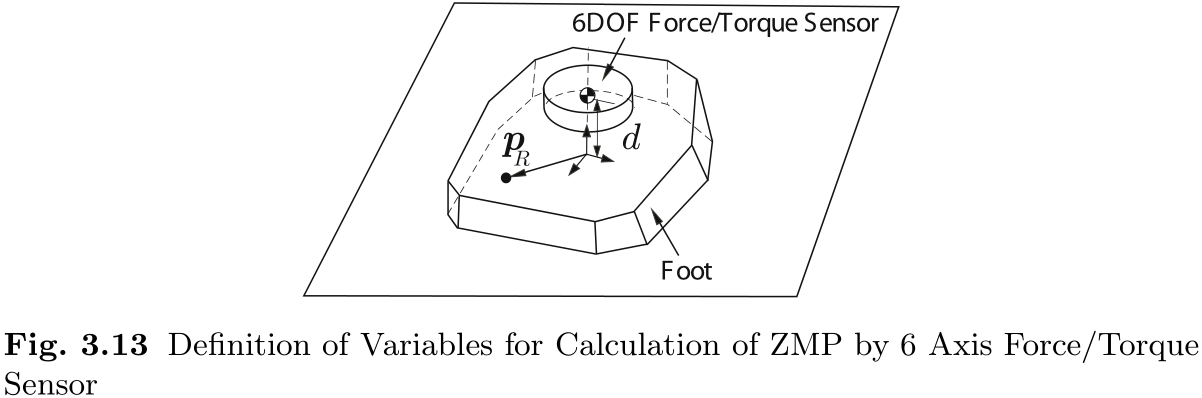
如图 3.13 所示, 假设 ZMP 在左右脚的位置分别为
其中
② 通过多个力传感器测量 ZMP
接下来, 我们将介绍使用多个力传感器测量 ZMP 的方法. 图 3.14 展示了仿人机器人 H5 [70]. 为了使脚部轻便, 我们使用了 12 个力传感寄存器: FSR 和由两个铝平面夹住的 sorbothane 来测量 ZMP (图 3.14(b)) . 由于电阻随外力变化, FSR 可用作一维力传感器来测量地面反作用力的垂直分量.
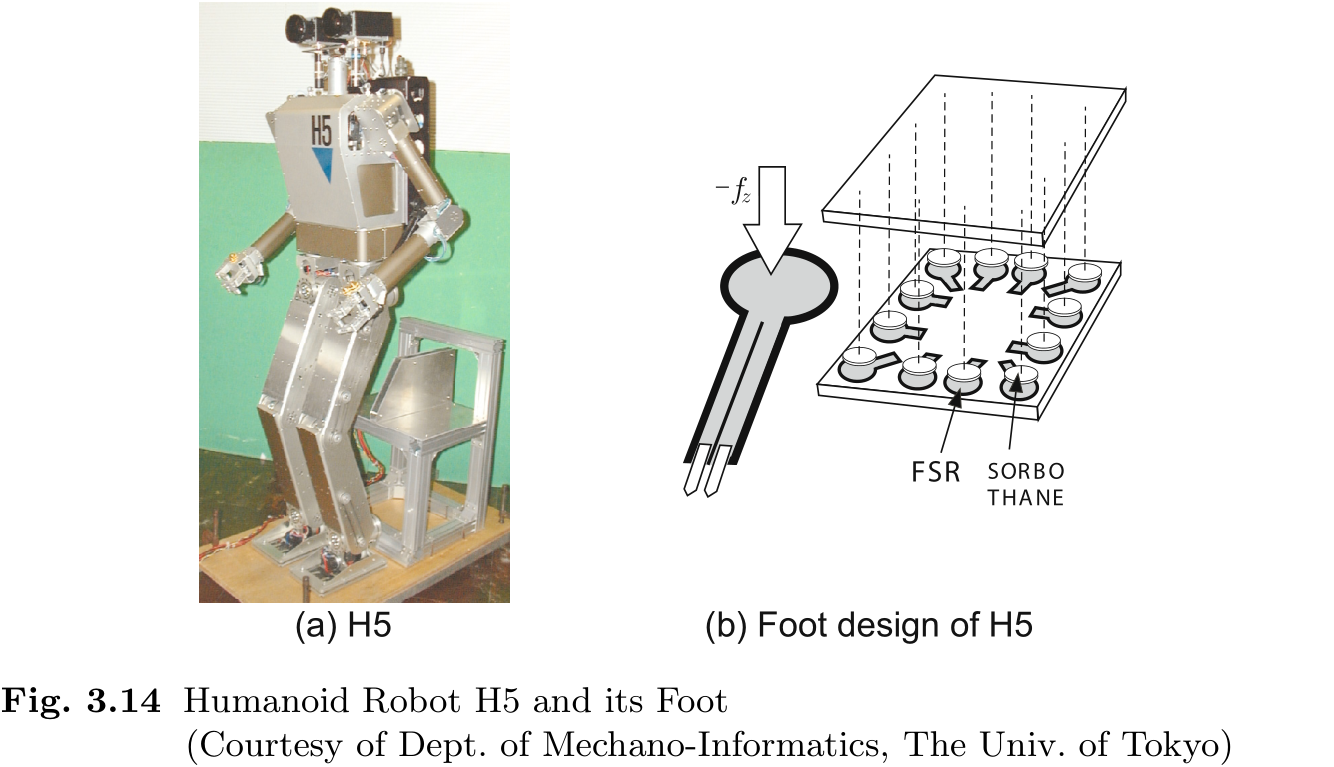
为了测量 ZMP, 在 (3.24) 和 (3.25) 中将力的
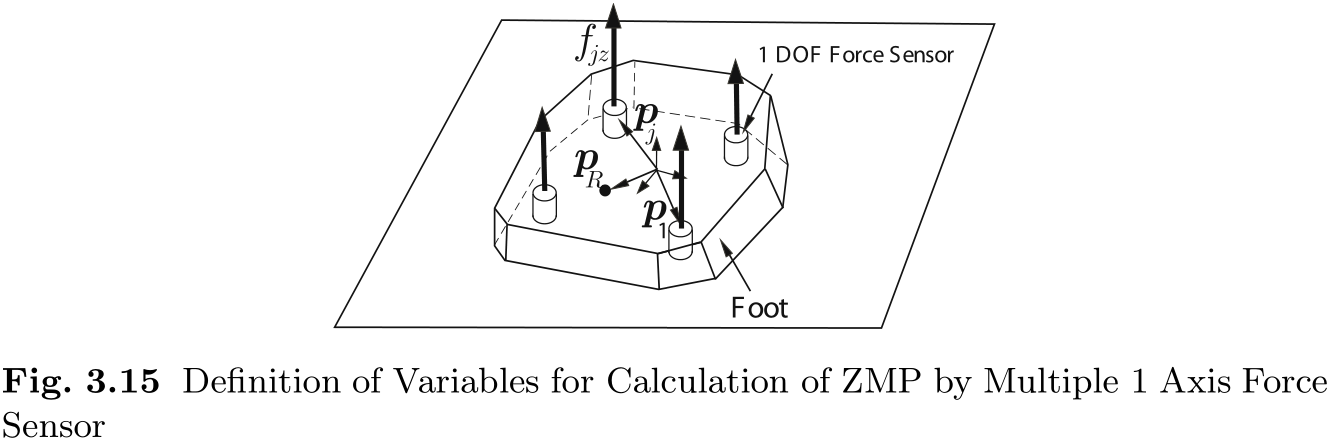
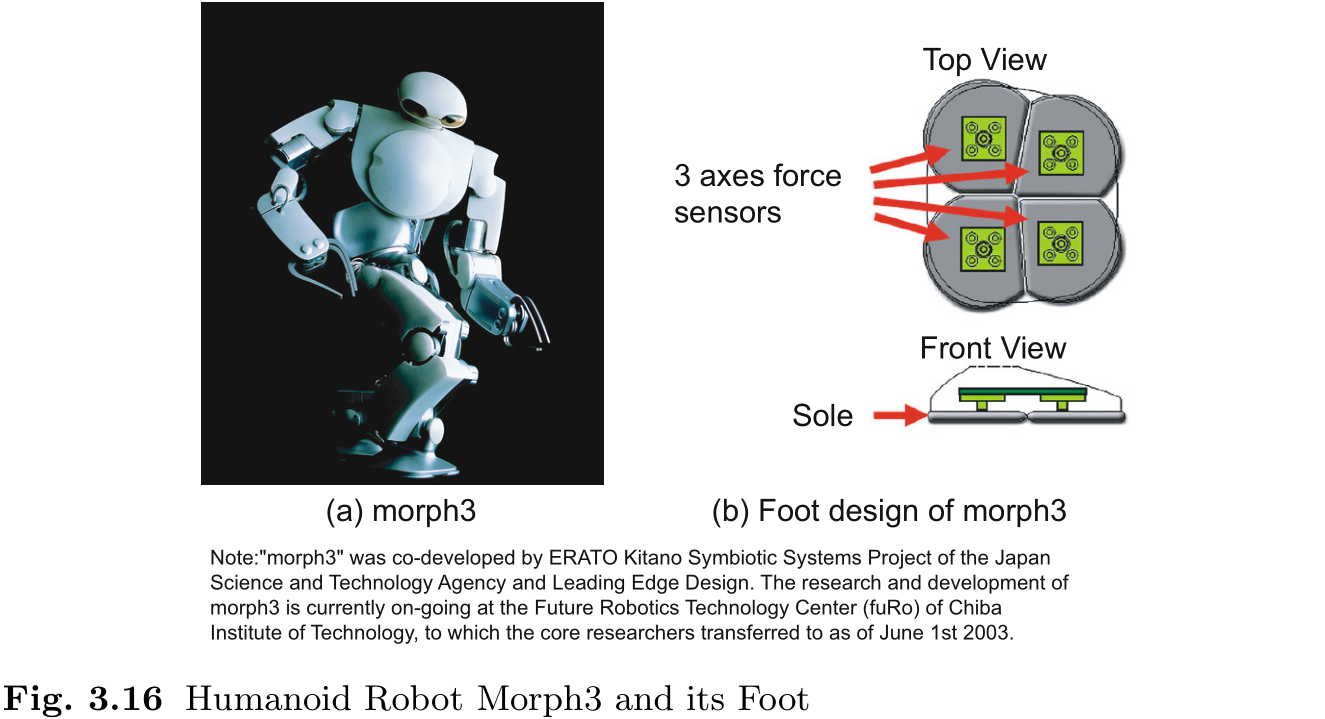
图 3.16 展示了仿人机器人 Morph3 及其脚[129, 120]. Morph3 使用连接在每只脚上的四个三轴力传感器测量 ZMP (图 3.16(b)) . 三轴力传感器测量的是施加在脚底的分为四个部分的三维力. 通过使用该测量系统, 我们可以获得接触点的测量结果. 为了计算每个脚的 ZMP, 将 (3.24) 和 (3.25) 中的力矩元素
3.2.3 双脚接触的 ZMP
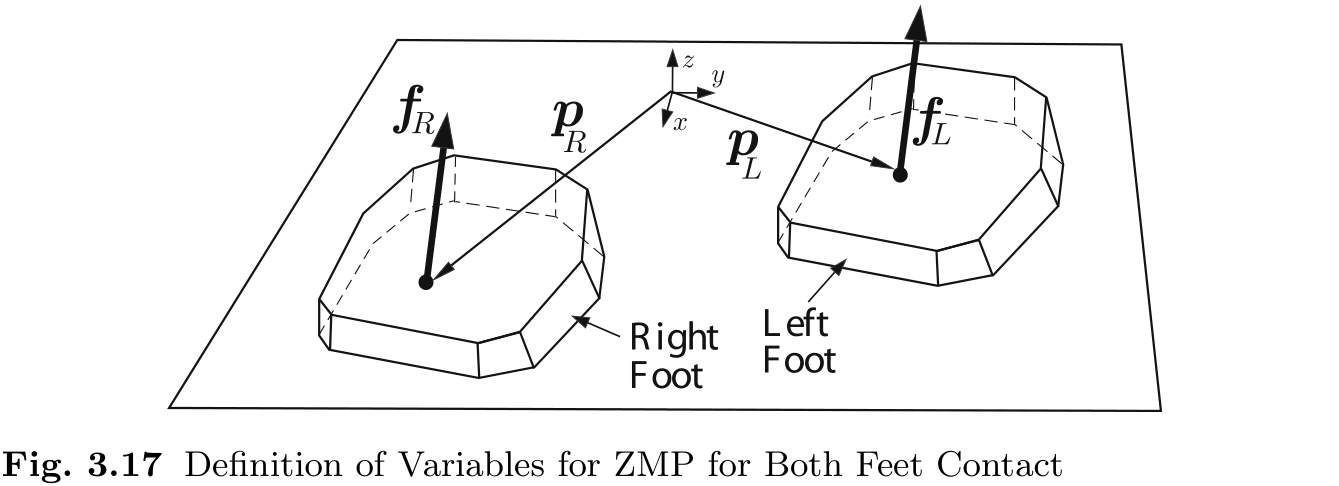
到上一节为止, 每只脚的 ZMP 位置可以用
其中
在单支撑阶段, 由于地面反作用力的垂直分量变为零, 因此使用 (3.30) 和 (3.31) 计算出的 ZMP 与支撑脚的 ZMP 相吻合. 由此得出
在本节的最后, 我们要说明的是, 在考虑仿人机器人的平衡时, 我们可以使用 (3.30) 和 (3.31), 将双脚都考虑在内, 而无需考虑支撑脚.
3.3 仿人机器人的动力学
根据前面的讨论, 我们可以用 ZMP, 线性力和通过 ZMP 的垂直线的力矩来表示作用在仿人机器人上的地面反作用力. 本节将讨论地面反作用力与机器人运动之间的关系. 在给出基本方程后, 我们将解释其原理. 最后, 我们将展示一些计算算法.
① 基本物理参数
让我们考虑一个具有任意结构的仿人机器人. 虽然它可以由金属, 塑料和陶瓷等材料组成, 但我们假定可以清楚地识别机器人和其他东西. 我们可以将以下十个物理参数分为四组:
- 质量: 机器人总质量.
[kg] - 质心: 机器人的质心.
[m] - 动量: 机器人平移运动的度量.
[Ns].
我们通常称之为线动量, 以区别于角动量.
- 角动量: 测量机器人绕原点的旋转运动.
[Nms]
我们随后将阐明什么是动量
我们将解释每个方程的含义.
② 平移运动的动力学
关于平移运动的第一个方程给出了质心速度和动量之间的关系
反之, 我们可以从这个等式中看出, 动量为 (总质量)
其中,
让我们确认一下, 它与 质量
速度 得到的单位 [kgm/s] 是一致的.
牛顿在《自然哲学数学原理》中描述的第二运动定律最初是以 (3.34) 的形式表达的. 从 (3.34) 和 (3.33) 中消除
让我们考虑机器人所受的外部力. 重力平均作用在机器人的所有部件上, 其总和可视为作用在机器人质心
作为
的另一个例子, 我们可以考虑推物体时的反作用力和刮风时的阻力.
当机器人静止不动时, 由于重力与地面反作用力相平衡, 动量变化为 0. 如果地面反作用力消失, 机器人的动量就会在重力作用下迅速向下增加. 这就是自由落体运动.
③ 旋转运动的动力学
关于旋转运动, 我们可以得出以下方程
这个等式表明, 角动量的变化与机器人所受的外部力矩的总和
在机器人受到的力矩中, 重力产生的力矩为
让
绕原点的旋转运动方程可表示如下
作为力矩
3.3.2 动量
① 质心
无论机器人的结构多么复杂, 归根结底都是原子的集合. 假设一个仿人机器人由
设
对上式求导, 可得
其中,
这里, 上一节中的 (3.33) 可以由 (3.39) 和 (3.40) 得出.
② 动量动力学
我们将推导出机器人的动量动力学. 第
其中,
我们注意到, 由于第
考虑到上述关系并对机器人所有质点求和 (3.41), 一个质点受到的来自另一个质点的力将被抵消,
使用
我们证实, 机器人的动量并不取决于内力, 而是取决于外力. 我们注意到, 即使机器人是由柔性材料或液体组成的, 也可以始终满足这一方程, 而不依赖于机器人的结构.
3.3.3 角动量
① 角动量与线动量
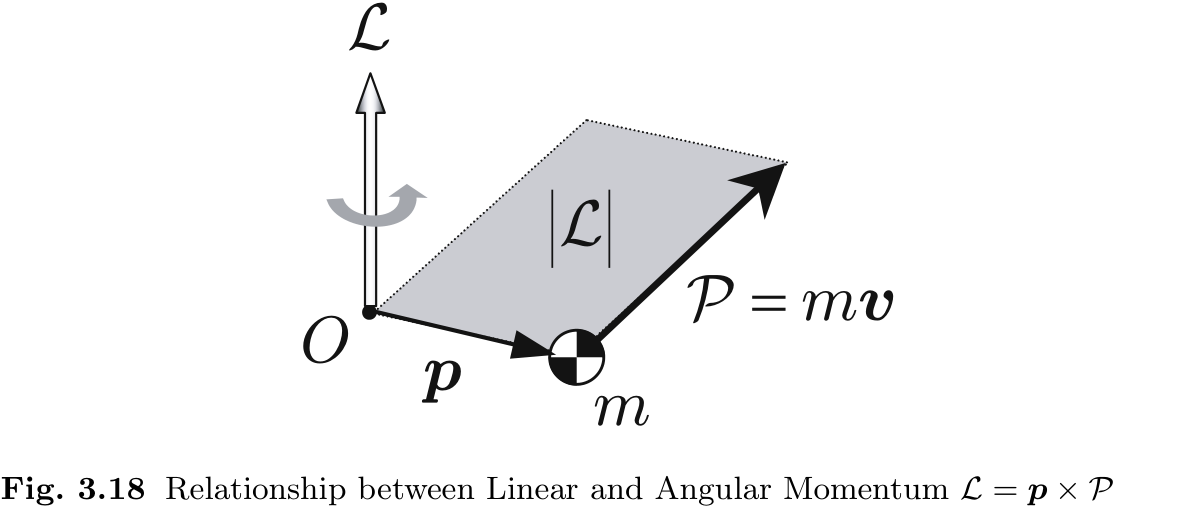
如图 3.18 所示, 第
我们应该注意以下两点.
- 角动量是一个向量, 在三维空间中用箭头表示.
与角速度一样, 它也是一个伪向量.
- 角动量不仅是旋转运动的属性. 例如, 利用上式, 我们可以计算出以恒定速度直线运动的质点的角动量. 在这种情况下, 角动量保持不变 (角动量守恒) .
让我们考虑一个由原点以外的向量
机器人绕参考点的总动量为
因此,
例如, 当我们计算机器人围绕质心的角动量时, 就可以使用这个方程.
② 角动量动力学
现在我们得到角动量的动力学. 将 (3.43) 随时间微分, 得到
由于右边的第一项为 0, 我们得到
将上一节的运动方程 (3.41) 代入 (3.46), 可得
由于总角动量是各质点角动量之和
其中右边第一项的表达式为
其中,
因此, (3.48) 右边的第一项变为零
由于上式的右边表示的是外力对原点的力矩, 因此我们用
我们证实, 关于原点的角动量并不取决于内力, 而是取决于从机器人外部施加的力矩. 此外, 无论机器人的结构和材料如何, 该方程始终满足要求.
本书对质点动量和角动量的推导沿用了 Goldstein 的经典力学 (Classical Mechanics) [36].
3.3.4 刚体的角动量和惯性张量
刚体是一种理想的物体, 具有足够的硬度, 不会变形. 在分析机器人时, 通常假定它是由一些通过关节连接的刚体组成的.
虽然这只是一个近似值, 但即使机器人的模型是刚体的总和, 分析也足够精确.
现在我们来计算刚体的角动量. 假设刚体漂浮在空间中, 不受外力影响而旋转. 如第 2 章所述, 刚体的旋转速度可用角速度向量
将 (3.50) 代入 (3.43), 我们可以通过以下公式计算出刚体的总角动量
我们可以看到, 刚体的角动量由角速度向量乘以系数矩阵表示. 这个矩阵称为惯性张量, 记为
从其定义可以看出,
我们只需写出连续系统的 (3.51), 就能得到具有任意形状和任意密度分布
我们不需要计算任何密度均匀物体的惯性张量, 因为典型形状的惯性张量可以在各种教科书或网站上找到. 例如, 对于边长分别为
假设一个长方体的每条边长为 0.1 × 0.4 × 0.9 [
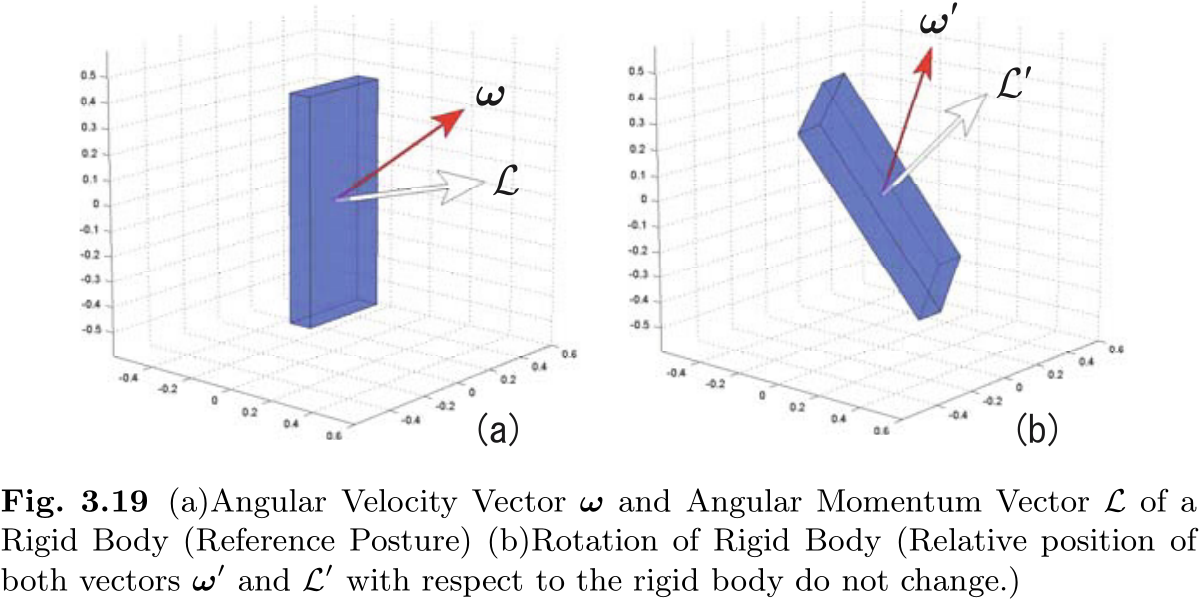
图 3.19(a) 显示了该物体的角动量向量, 其角速度为
现在, 图 3.19(b) 显示了刚体通过乘以旋转矩阵
另一方面, 根据 (3.52), 参考姿态的角动量计算公式为
将上式代入 (3.56), 并用 (3.55) 将
我们可以认为
3.3.5 计算机器人质心
根据上述讨论, 我们将计算动力学的物理参数. 我们首先展示计算机器人质心的方法. 给定所有链节的位置和朝向, 可以通过以下步骤计算出来:
- 步骤 1. 计算每个链节在世界坐标中的质心位置.
- 步骤 2. 计算每个链节的质量对原点产生的力矩之和.
- 步骤 3. 用力矩除以总质量, 即可得到质心的位置.
假设第
其中,
计算世界坐标原点力矩的程序如图 3.20 所示. 通过该程序, 我们可以计算出机器人的质心, 如图 3.21 所示.
图 3.20 calcMC.m 计算绕世界坐标原点的总力矩
1
2
3
4
5
6
7
8function mc = calcMC(j)
global uLINK
if j == 0
mc = 0;
else
mc = uLINK(j).m * (uLINK(j).p + uLINK(j).R * uLINK(j).c);
mc = mc + calcMC(uLINK(j).sister) + calcMC(uLINK(j).child);
end图 3.21 calcCoM.m 计算质心位置
1
2
3
4
5function com = calcCoM()
global uLINK
M = TotalMass(1);
MC = calcMC(1);
com = MC / M;
3.3.6 计算链节线速度和角速度
在下面两个小节中, 我们将计算机器人的总动量和总角动量. 在准备过程中, 我们需要获得组成机器人的所有链节的线速度和角速度.
与前一章中的正向运动学一样, 让我们来计算与其父链节相连的链节的速度. 我们假设父链节
图 3.22 显示了使用上述方程和递归算法计算所有链节的速度和角速度的 Matlab 代码.
图 3.22 ForwardVelocity.m 速度的正向计算
1
2
3
4
5
6
7
8
9
10function ForwardVelocity(j)
global uLINK
if j == 0 return; end
if j ~= 1
i = uLINK(j).mother;
uLINK(j).v = uLINK(i).v + cross(uLINK(i).w, uLINK(i).R * uLINK(j).b);
uLINK(j).w = uLINK(i).w + uLINK(i).R * (uLINK(j).a * uLINK(j).dq);
end
ForwardVelocity(uLINK(j).sister);
ForwardVelocity(uLINK(j).child);
3.3.7 计算机器人动量
由
其中,
其中
图 3.23 calcP.m 计算机器人的动量
1
2
3
4
5
6
7
8
9function P = calcP(j)
global uLINK
if j == 0
P = 0;
else
c1 = uLINK(j).R * uLINK(j).c;
P = uLINK(j).m * (uLINK(j).v + cross(uLINK(j).w, c1));
P = P + calcP(uLINK(j).sister) + calcP(uLINK(j).child);
end
3.3.8 计算机器人角动量
由 N 个链节组成的机器人的角动量为
其中
其中,
图 3.24 calcL.m 计算机器人对原点的角动量
1
2
3
4
5
6
7
8
9
10
11function L = calcL(j)
global uLINK
if j == 0
L = 0;
else
c1 = uLINK(j).R * uLINK(j).c;
c = uLINK(j).p + c1;
P = uLINK(j).m * (uLINK(j).v + cross(uLINK(j).w , c1));
L = cross(c, P) + uLINK(j).R * uLINK(j).I * uLINK(j).R' * uLINK(j).w;
L = L + calcL(uLINK(j).sister) + calcL(uLINK(j).child);
end
3.4 根据机器人运动计算 ZMP
利用上述机器人动力学理论和算法, 我们可以计算出机器人给定运动的 ZMP.
3.4.1 ZMP 推导
让我们回顾一下, 地面反作用力可以用 ZMP (
地面反作用力与动量之间以及地面反作用力矩与角动量之间的关系 (第 3.3.1 节) 分别为
将 (3.67) 和 (3.68) 代入 (3.69), 并根据
具体来说, 该方程的第一行和第二行分别为
其中
在这里, 我们利用了关于 ZMP 的力矩的
根据
其中
例如, 当机器人静止不动时, 我们有
ZMP 与质心的地面投影重合.
图 3.25 显示了利用 (3.73) 和 (3.74) 计算 ZMP 的程序.
图 3.25 calcZMP.m 计算 ZMP
1
2
3
4function [px,py] = calcZMP(c,dP,dL,pz)
global M G
px = (M*G*c(1) + pz * dP(1) - dL(2))/(M*G + dP(3));
py = (M*G*c(2) + pz * dP(2) + dL(1))/(M*G + dP(3));
这里, dP (
3.4.2 使用近似法计算 ZMP
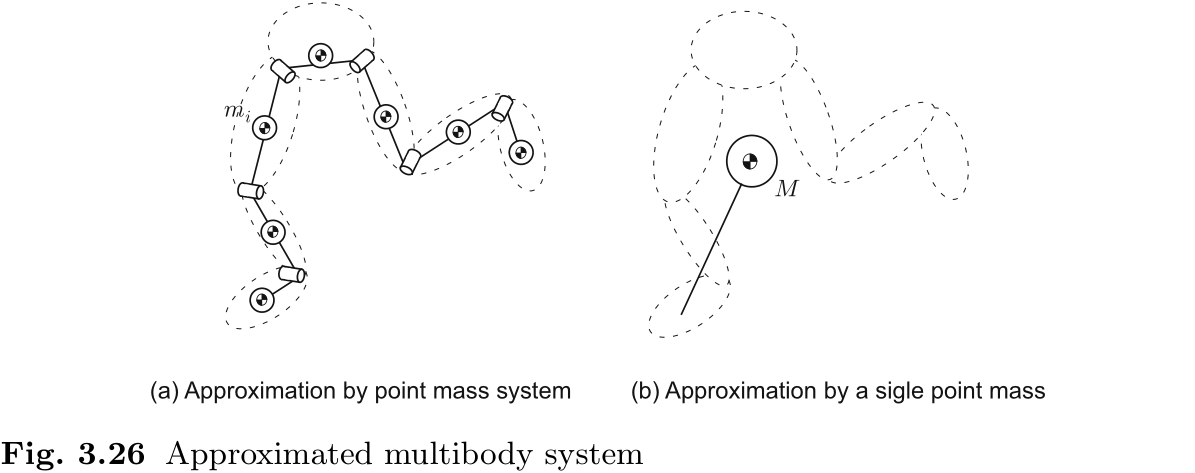
我们将介绍使用简化模型计算 ZMP 的方法. 图 3.26(a) 中的机器人模型忽略了每个链节关于其质心的惯性张量的影响, 并假定机器人是质点的总和. 在这种情况下, 关于原点的角动量由以下公式给出
将 (3.77) 代入 (3.73) 和 (3.74) , ZMP 可表示为
其中
接下来, 在图 3.26(b) 所示的模型中, 整个机器人以一个质点为模型. 在这种情况下, 关于原点的动量和角动量由以下公式给出
其元素为
将上式代入 (3.73) 和 (3.74), ZMP 的计算公式为
我们将在第 4 章中使用 (3.84) 来生成双足步态.
3.5 关于 ZMP 的一些说明
3.5.1 两种解释
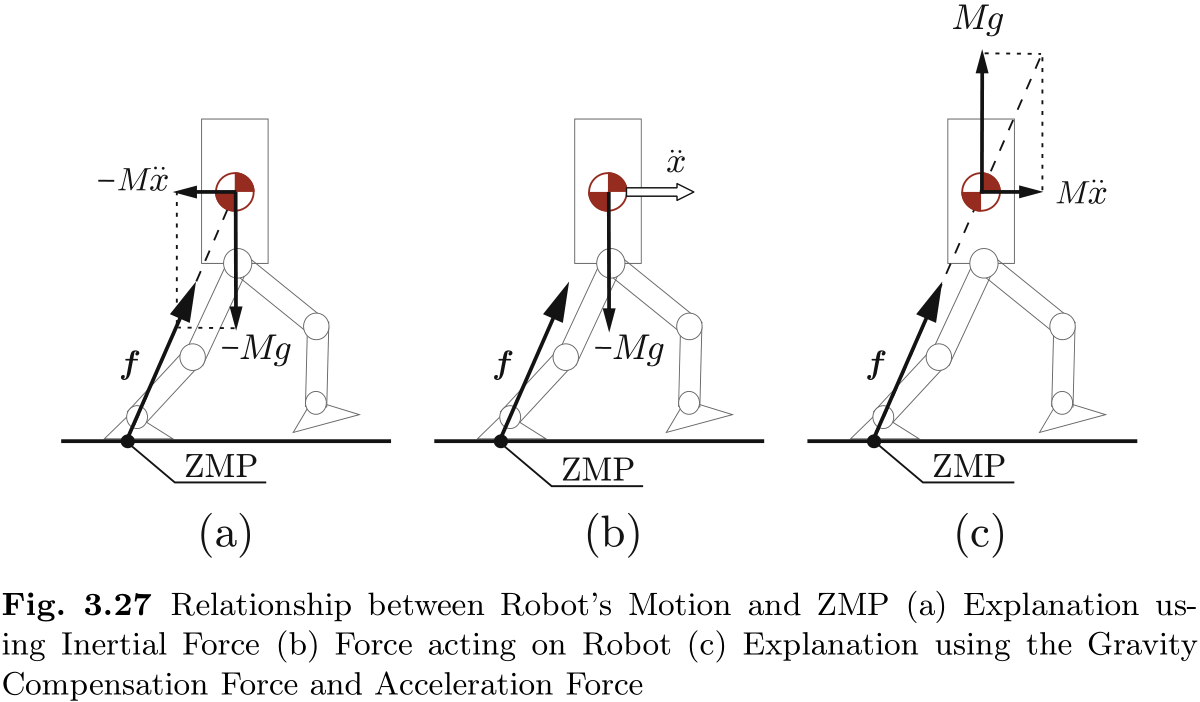
为了直观地解释机器人运动与 ZMP 之间的关系, 通常会引入图 3.27(a) 这样的质点模型. 这里,
3.5.2 由于质心的加速度, ZMP 是否存在于支撑多边形之外?
经常会有这样的讨论: "根据机器人的运动, ZMP 是否会离开支撑多边形?当然, 结论是 "ZMP 永远不会存在于支撑多边形之外"[37, 88].
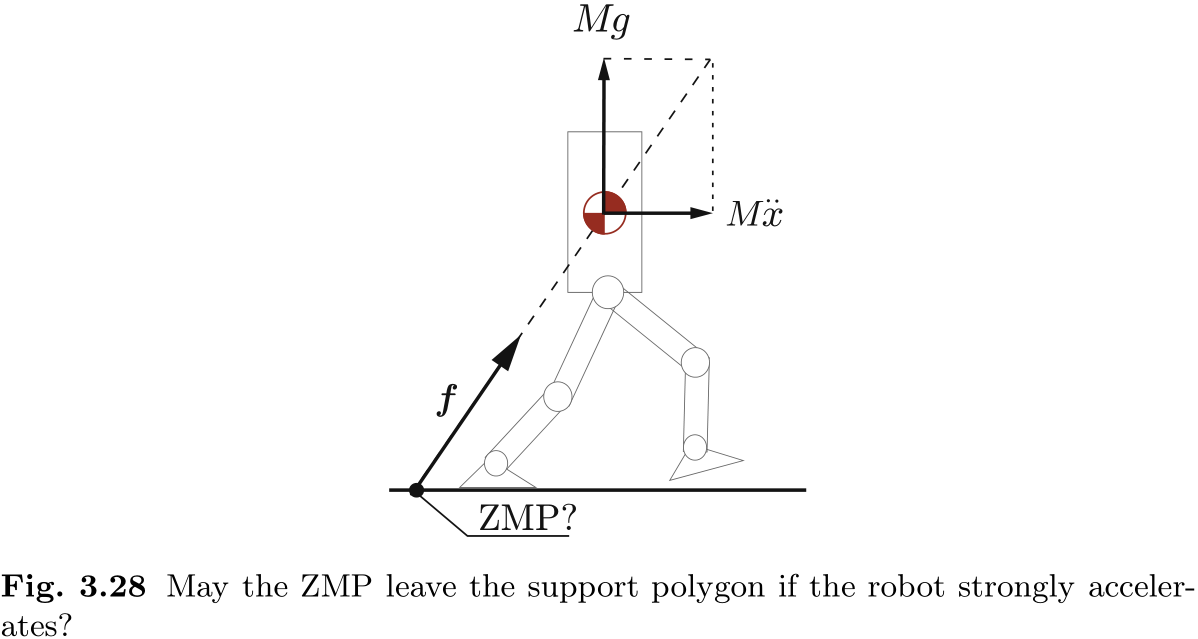
然而, 如图 3.28 所示, 当以质点为模型的机器人以高加速度水平移动时, 会发生什么情况呢?如果鞋底与地面之间有足够的摩擦力, 水平加速度就不会受到阻碍. 如上所述, ZMP 存在于重力和惯性力所定义的直线上, 将
机器人的加速度越大, ZMP 就离支撑多边形越远!
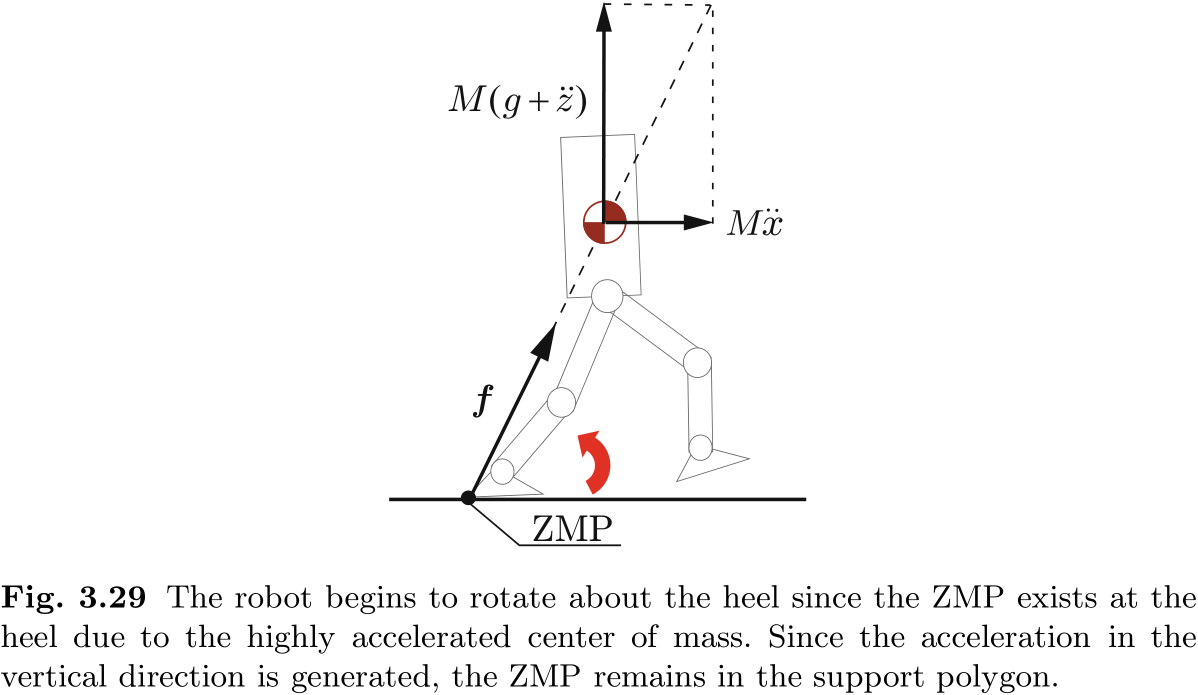
我们将利用图 3.29 解释这一讨论中的错误. 由于质心高度加速, ZMP 被移到了脚跟处. 然后, 机器人将开始围绕脚跟旋转. 由于垂直方向上会产生加速度, 所以
由于
这就是本田汽车公司提出的 "ZMP 模式控制 "的原理. 有关更具体的讨论, 请参见第 152 页.
更具体地说, 要利用 (3.73) 和 (3.74) 计算给定机器人运动的 ZMP, 我们需要引入以下任一先验:
- 先验 A: 由于鞋底固定在地面上, 因此可以保持鞋面与地面的接触.
- 先验 B: 可以测量机器人的姿态, 绝对线速度和角速度.
根据机器人的模拟运动计算 ZMP 时, 我们通常使用先验 A. 在这种情况下, 由 (3.73) 和 (3.74) 得出的 ZMP 可能存在于支撑多边形之外.
这种 ZMP 被称为 IZMP (Imaginary ZMP) [89].
但是, 真正的机器人要实现这种情况, 鞋底必须通过吸盘或磁铁固定在地面上. 普通的仿人机器人无法实现这种情况, 因为鞋底会与地面脱离接触.
另一方面, 要使用 (3.73) 和 (3.74) 计算真实机器人的 ZMP, 我们需要引入先验 B. 该 ZMP 与脚部力/力矩传感器测得的 ZMP 相吻合, 绝不会存在于支撑多边形之外.
3.5.3 ZMP 的局限性
由于 ZMP 等同于压力中心, 因此其物理意义非常明确. 此外, ZMP 与机器人的线/角动量之间的关系也可以用一个简单的方程来表示. 因此, ZMP 是在有足够摩擦力的平地上规划行走运动的有力工具.
另一方面, ZMP 不能用于以下情况:
- [A] 我们要确定鞋底在地面上是否会打滑.
- [B] 地面不平坦.
- [C] 仿人机器人的手臂或双手与环境接触.
对于 [A], 我们无法仅通过 ZMP 信息来判断地面的滑动情况, 如第 3.1 节所述. 另一方面, 对于 [B] 和 [C], 虽然 ZMP 的位置会随着摩擦力的变化而变化, 但在给定机器人运动的情况下, 存在无法唯一确定摩擦力的情况. 此外, 接触点之间的内力也不会影响 ZMP 的位置.
由于 ZMP 是地面反作用力的二维信息, 而确定接触状态的转换需要力/力矩的六维信息, 因此出现了上述问题.
至于 [B] 和 [C], 则提出了侧重于凸多边形边缘力矩的方法 [80]. 然而, 问题仍然在于摩擦力的处理.
在此, 我们介绍一种考虑到全部六维力/力矩的方法 [39].
假设机器人是一个单一刚体. 在向量
其中,
由于
3.6 附录: 凸集与凸包
我们在第 3.1.1 节中介绍了凸集和凸包, 以定义支撑多边形, 并在第 3.1.3 节中介绍了凸包, 以显示 ZMP 的区域. 在机器人研究领域, 凸包用于机器人手的抓取分析和避免物体间的碰撞. 此外, 在数学编程研究领域, 凸集和凸包也是重要的基本概念. 有关更具体的讨论, 请参考[104].
例如, 凸集和凸包可以定义为无界集. 但是, 由于鞋底与地面的接触面积是有界的, 因此我们在本书中只对有界集进行解释.
凸集:
对于任意
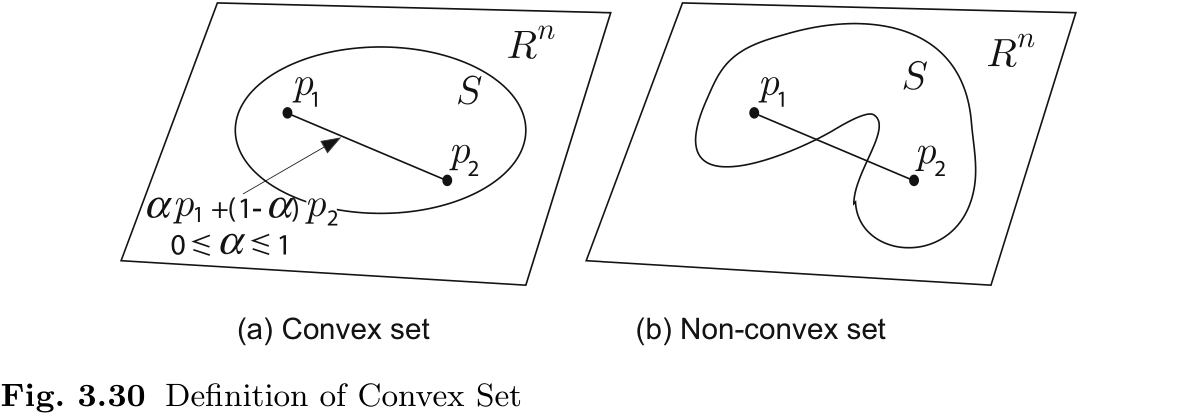
凸包:
对于
让我们考虑凸包是有界凸多面体的情况. 设