本文为书籍 Introduction to Humanoid Robotics 的汉化, 主要借助翻译器 DeepL.
另外, 原书有管贻生教授的译作版本:《仿人机器人》(清华大学出版社, 2007年). 强烈推荐.
2 运动学 (Kinematics)
分析链节的位置和姿态与机构的关节角度之间关系的理论称为运动学. 它是机器人学的基础, 但同样的理论也用于计算机制图. 二者都需要能够在三维空间中清晰表现运动物体的数学和算法.
2.1 坐标变换 (Coordinate Transformations)
图 2.1 展示了在仿人机器人项目 [65] 期间开发的仿人机器人 HRP-2. 它的高度为 154 厘米, 包括电池在内的重量为 58 千克. 仅靠电池, 它就能行走约一小时. HRP-2 共有 30 个可独立控制的关节. 图 2.1(b) 显示了各关节的名称及其局部坐标位置.

2.1.1 世界坐标 (World Coordinates)
我们的首要任务是明确机器人各部分的位置. 为此, 我们在机器人初始位置的正下方定义一个特殊点(实际上, 它是通过腰部关节局部坐标原点的垂直线与地板的交点), 如图 2.2 所示. 以这一点为原点, 我们定义了一个固定坐标系, 其
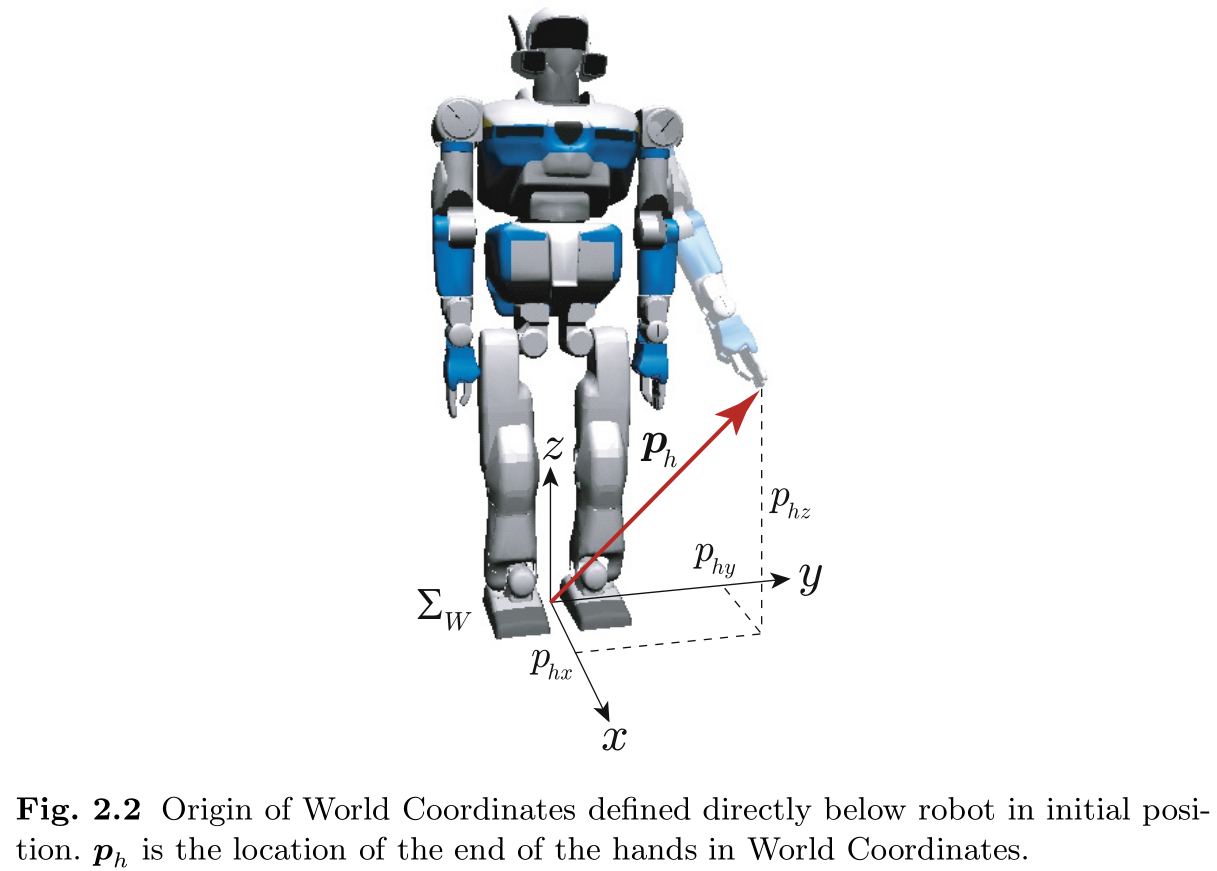
我们将这些坐标命名为
使用世界坐标定义的位置称为绝对位置. 例如, 我们用以下三维向量来描述图 2.2 中左手尖端的绝对位置
我们还将使用 "绝对姿态" 和 "绝对速度" 这两个术语来说明它们是在世界坐标中定义的.
2.1.2 局部坐标与齐次变换
让我们来看看手尖位置
在图 2.3(b) 的张开手臂姿势中, 可以通过引入另一个向量
手通过向量从
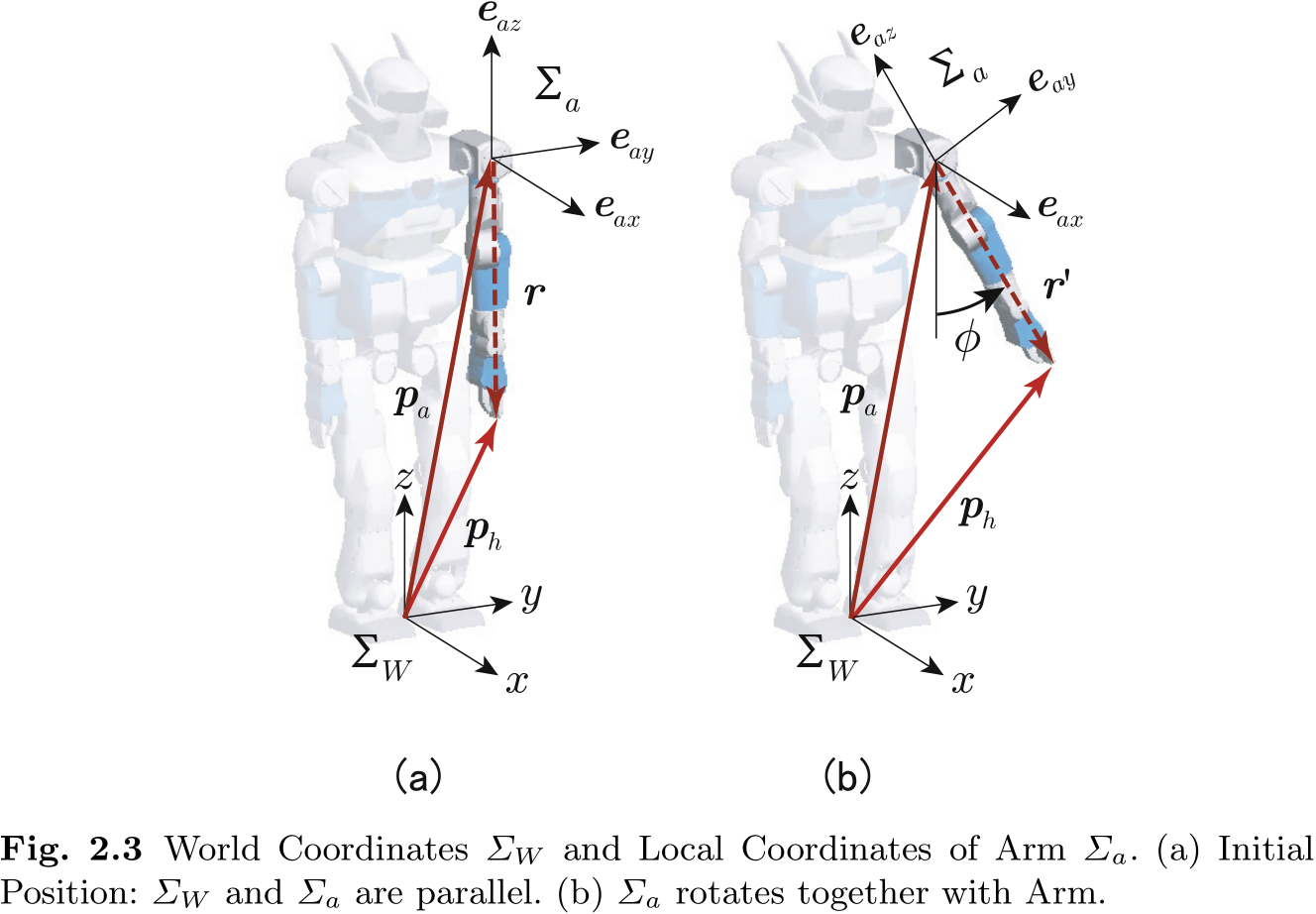
如图 2.3 所示, 让我们设想一个连接在左肩上的局部坐标系
局部坐标系
肩部旋转量
由于是绕
利用矩阵
换句话说, 向量乘以矩阵
现在, 让我们定义手端点在局部坐标系
在图 2.3 所示的示例中,
为了描述左臂末端的位置, 我们使用了两种不同的符号.
- 从世界坐标
看手末端 的位置. - 从局部坐标
看手末端 的位置.
两者之间的关系如下. 根据 (2.1), (2.4) 和 (2.5), 我们可以得到
公式 (2.6) 也可改写为
在这里, 我们在矩阵中添加了 0 和 1 以匹配维数, 使其符合 (2.6). 等式右侧的
这样的矩阵称为齐次变换矩阵.
同样的矩阵在计算机图形学中被称为仿射变换矩阵. 两者之间存在区别, 因为在仿射变换中,
不一定是一个简单的旋转矩阵 ( 第 2.2 节) , 还可能包括缩放和剪切.
齐次变换矩阵可将用手臂局部坐标描述的点转换为世界坐标
需要注意的是, 点
2.1.3 局部坐标系上的局部坐标系
我们可以定义一个以另一个局部坐标系为父坐标系的局部坐标系. 图 2.4(a) 显示了一个以
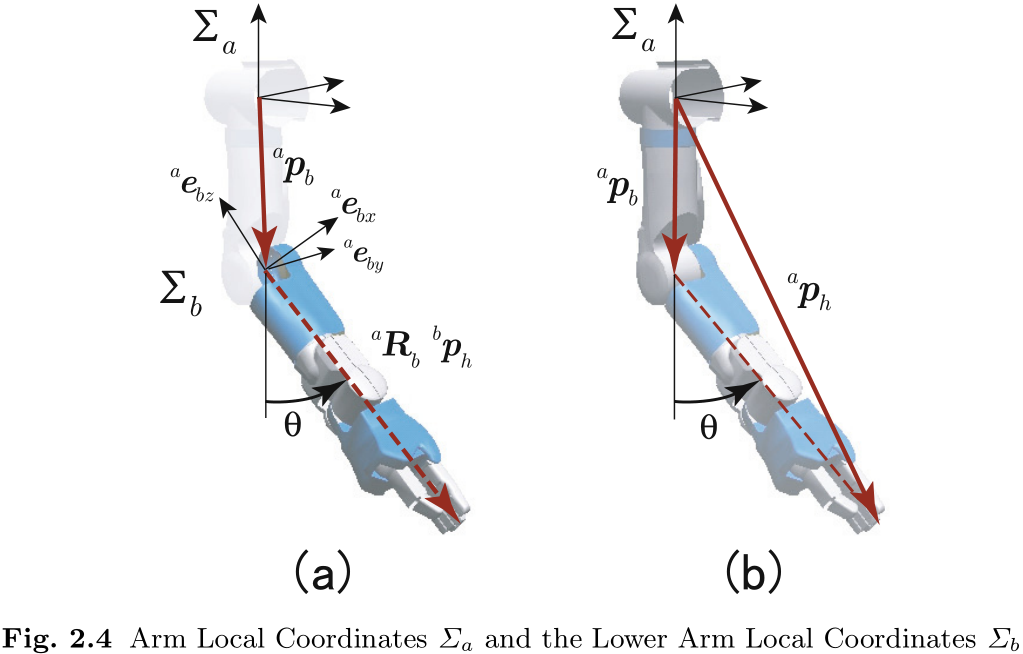
由于肘部绕
将
在这里, 我们对齐次变换
注意,
将 (2.10) 的结果与 (2.7) 结合起来, 我们就得到了将
让我们把等式右边的齐次变换乘积定义为一个矩阵, 并称之为
矩阵
2.1.4 齐次变换与链式法则
我们上面描述的内容可以加以推广. 假设我们有一个连接局部坐标
重复上述过程, 我们可以得到以下等式
这里的
这种乘以齐次变换以计算坐标变换矩阵的方法被称为链式法则 [87]. 链式法则使我们能够计算具有多个关节的手臂的运动学, 而不会过于复杂.
2.2 旋转运动的特性
在上一节中, 我们用一个
2.2.1 滚动角 (Roll) , 俯仰角 (Pitch) 和偏航角 (Yaw) 记号
旋转的基本原理是绕
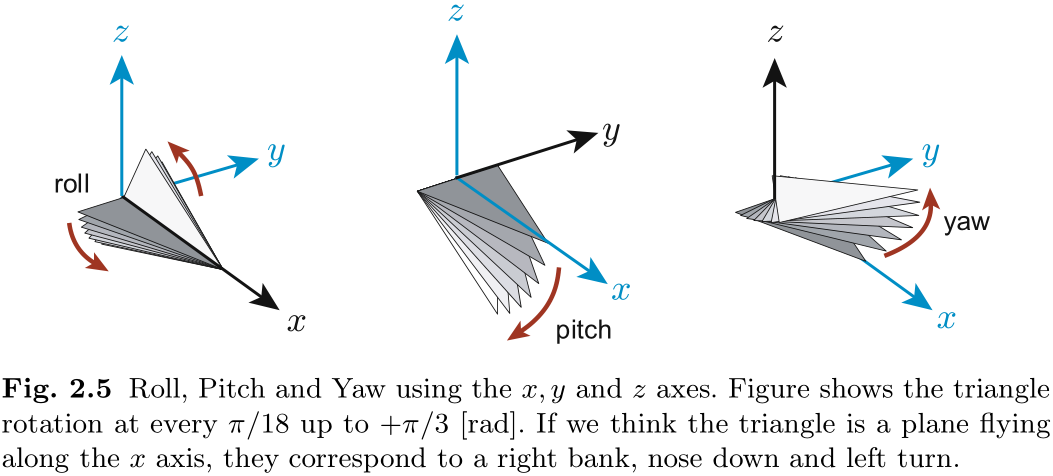
下面列出了旋转轴, 名称和常用符号.
| Rotation Axis | Name | Notation |
|---|---|---|
| Roll | ||
| Pitch | ||
| Yaw |
要使物体滚动, 俯仰和偏航一个给定角度, 我们需要使用以下矩阵
如果我们将一个点
我们可以将其改写为
在此, 我们引入以下符号
其中,
矩阵
由于 "滚动-俯仰-偏航" 符号易于理解, 因此常用于记录船舶, 飞机和机器人的姿态.
2.2.2 旋转矩阵的意义
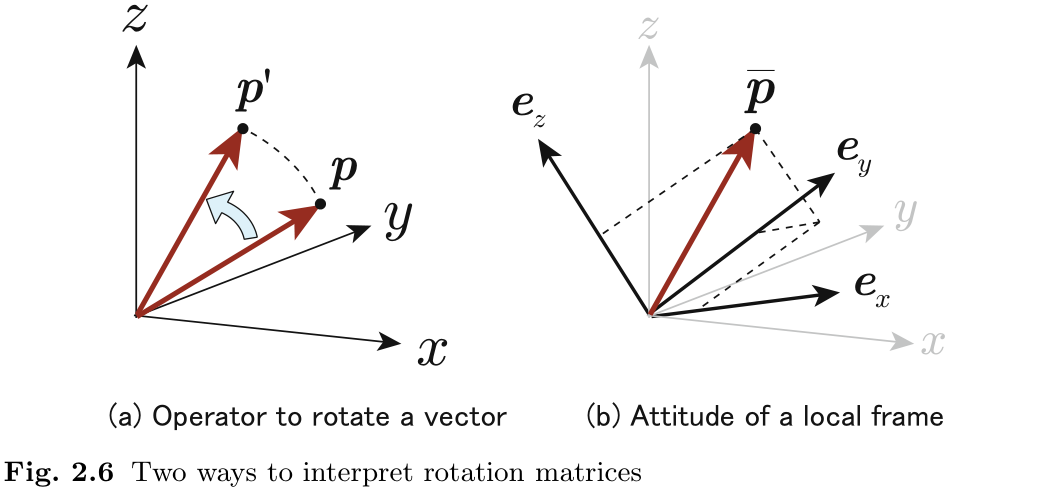
有两种不同的方法来解释旋转矩阵. 一种是作为旋转向量的算子. 图 2.6(a) 显示了向量
其中
解释
该点在世界坐标中表示为
在这种情况下, 我们只是改变了一个静止点的视角, 而没有任何实际的运动.
我们怎样才能弄清旋转矩阵用于哪种含义, (1) 旋转向量的算子, 还是 (2) 局部坐标系的姿态? 我们可以通过检查计算前后该点是否存在于相同的坐标空间来了解. 不过, 大多数情况下, 这一点从上下文中就能看出来.
2.2.3 计算旋转矩阵的逆矩阵
假设我们有一个显示本地坐标系姿态的旋转矩阵. 我们将把该坐标系的单位向量定义为
这里的
由此我们可以肯定地说,
因此, 当我们对旋转矩阵进行转置时, 就会得到它的逆矩阵. 具有这种特性的矩阵称为正交矩阵.
2.2.4 角速度向量
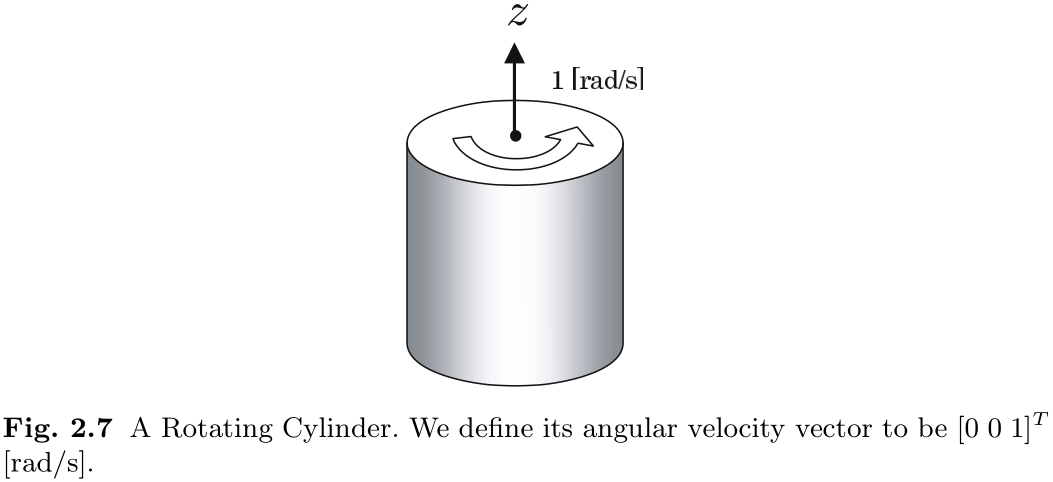
接下来, 我们将定义一种在三维空间中记录旋转速度的方法. 最简单的例子如图 2.7 所示. 该图显示一个圆柱体以 1 [rad/s] 的速度绕 Z 轴旋转. 在这种情况下, 该物体的旋转速度
这就是角速度向量. 该向量中的每个元素的单位都是 [rad/s].
角速度向量 (
被定义为单位向量 标量值 设
为旋转轴上的单位向量, 为旋转速度 (标量值) . 那么物体的角速度向量就是它们的乘积 描述旋转物体上所有点的速度 令
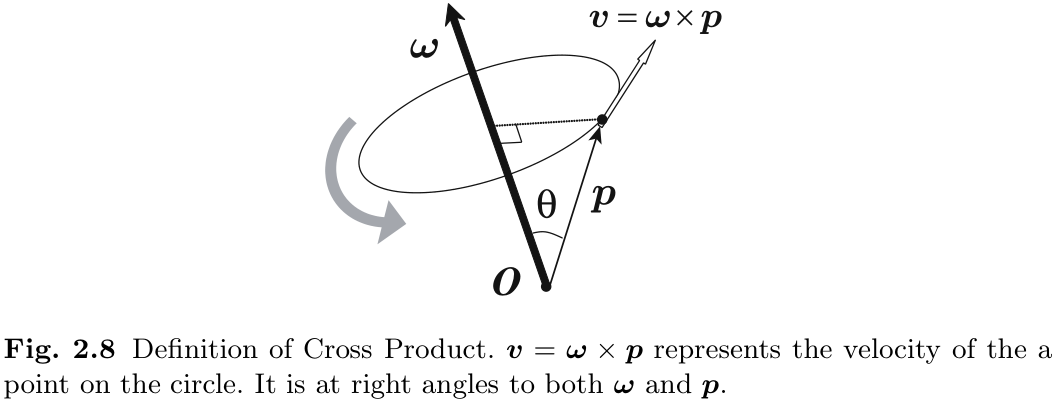
为一个向量, 表示物体表面上的给定点 . 我们还可以将该向量的基点定义为旋转轴上的某处. 在这种情况下, 点的速度将由 描述. 算子是两个向量的叉积或外积, 其定义如下. ![]()
通过使用
和 这两个向量, 我们可以得到一个新的向量 , 它具有以下特征 (图 2.8) 然而, 有两个向量满足这一条件, 因此我们使用右手螺旋定则, 选择符合右手螺旋转动时移动方向的那个向量. 可以表示为
称为 "
与 的叉乘". 当给定
和 的元素时, 可以计算出如下的叉乘. 作为练习, 我们还可以检验一下下面的等式是否可以从上面的等式中推导出来. 我们可以说, 叉乘的定义使其符合角速度的性质.
从这里开始, 我们将用它来计算力矩和角动量. 在电磁学中, 叉乘本身非常重要. 弗莱明右手定则和左手定则本身就是叉乘的结果.
下式为角速度向量增加了 "物理意义".
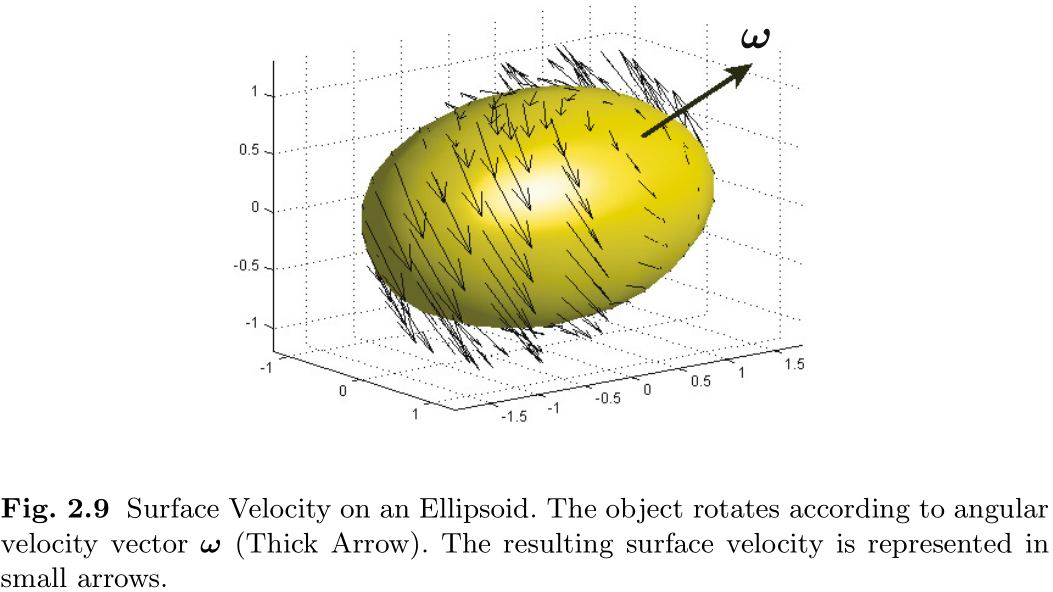
如图 2.9 所示, 我们用上面的方程将以
旋转的橄榄球形物体 (椭圆体) 的表面速度形象化. 在旋转物体上, 速度的大小和方向会因表面上的点的位置而不同. 角速度向量只用三个元素就能表示这一事实. 如果你想了解严格的数学事实, 角速度向量被称为伪向量 (或轴向向量) , 它与法向量的处理方法有些不同[105]. 不过在本书的范围内, 将其视为法向量是没有问题的. 从这个意义上说, 力矩和角动量也同样使用伪向量表示.
![]()
也可以旋转 让我们用某个旋转矩阵
将 (2.17) 的两边相乘 如果我们引入以下新的向量,
那么我们可以将 (2.20) 改写为
这与 (2.17) 中的定义相吻合, 因此我们可以看到,
是绕着由 定义的轴的新角速度向量. 因此我们可以说, 角速度向量可以通过旋转矩阵 直接变换. ![]()
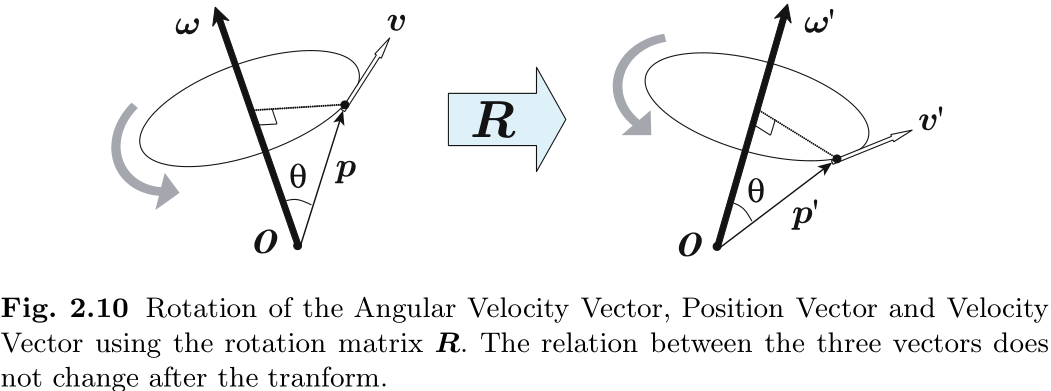
接下来, 让我们尝试使用相同的旋转矩阵
旋转一个角速度向量, 一个位置向量和相应的速度向量, 如图 2.10 所示, 由此得到 由于这三个向量之间的空间关系不会因旋转而改变, 因此必须保留叉乘的定义, 所以
将旋转后的向量
, 和 分别代入它们的原值 , 和 , 即可得出
2.2.5 旋转矩阵和角速度向量的导数
现在, 让我们研究一下角速度向量
如果我们将该方程关于时间求导, 就能得到该点在世界坐标空间中的速度. 在局部坐标空间中, 点
在这里, 我们利用
我们可以用这个等式来计算物体上一个顶点的速度.
从上一节中我们知道
如果我们还记得如下的叉乘计算公式 (2.19),
我们可以将其改写为
我们刚刚定义的矩阵有一个有趣的特征. 如果我们对这个矩阵进行转置, 就会得到只反转了符号的相同矩阵. 这样的矩阵被称为反对称矩阵, 并满足
通过比较 (2.26) 和 (2.28) 可以看出,
此外, 如果我们对这个方程关于时间求导, 就会得到以下结果.
矩阵的导数就是矩阵所有分量的导数. 必须注意不要改变乘法的顺序.
这就证明,
在本书中, 我们将从反对称矩阵中提取的三维向量称为
因此, 一个叉乘可以写成下面这样.
为了让这个等式更容易看懂, 我们可以把
很多教科书和论文都用
代替 , 以强调这是叉乘.
利用这些描述方法, 我们可以在 (2.26) 中用以下公式描述旋转矩阵与其角速度之间的关系
或
2.2.6 角速度向量与矩阵指数的积分
让我们来看看如何积分角速度向量并得到旋转矩阵. 将 (2.31) 的两边右乘
这个方程非常重要, 因为它给出了角速度向量和旋转矩阵之间的关系. 我们称这个方程为旋转基本方程. 该方程是矩阵
将上述公式代入 (2.33) 即可得出正确结论. 利用与指数函数的类比, 我们将用
这个无穷级数可以简化 [101]. 首先, 我们将
由于
公式 (2.36) 被称为罗德里格斯公式 (Rodrigues' formula) , 它可以直接从恒定角速度向量得到旋转矩阵. 这个方程和旋转基本方程是本书中最重要的方程.
方程 (2.36) 可以看作是给出了绕单位向量
该方程大量用于运动学计算.
请注意它与欧拉公式
的相似性, 理查德-费曼 (Richard Feynman) 称其为 "our jewel")[105].
2.2.7 矩阵对数
在定义了矩阵指数之后, 让我们来定义它的逆, 矩阵对数
它用于从给定的旋转矩阵中获取角速度向量. 在一秒钟内积分的角速度向量将等同于旋转矩阵所描述的旋转
实际计算结果为
给定
其中
利用矩阵指数和矩阵对数, 我们可以在两个给定的旋转矩阵
- 获取连接两个矩阵的旋转矩阵.
- 从旋转矩阵中获取等效角速度向量.
- 世界坐标中的角速度向量为:
- 插值为
2.3 三维空间中的速度
在本节中, 我们将平移运动添加到旋转运动中, 并考虑物体在三维空间中自由运动的速度.
2.3.1 单一物体的线速度和角速度
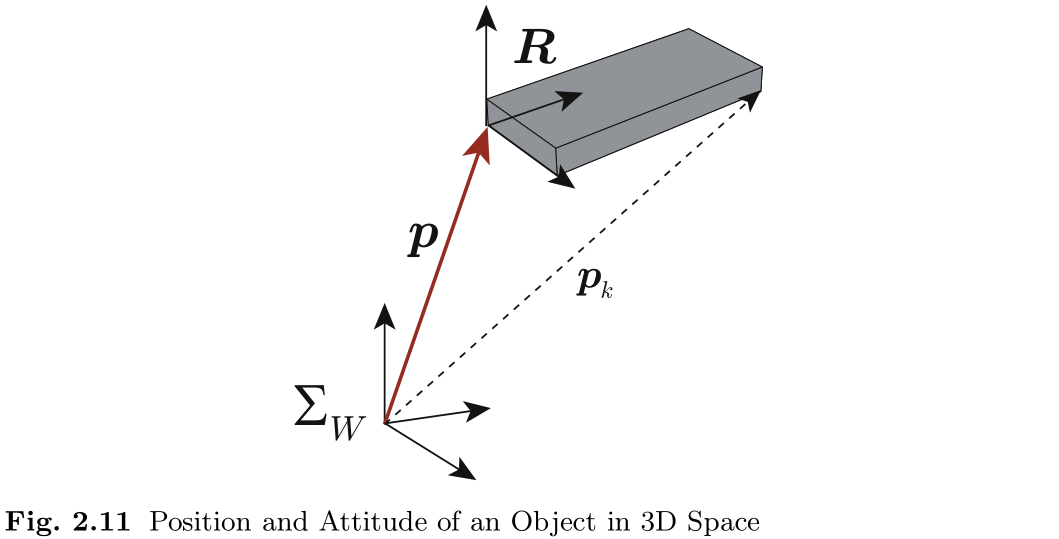
如图 2.11 所示, 物体在三维空间中的运动状态可以用物体中参考点
假设这个物体在空间中翻滚, 同时做平移和旋转运动. 点
其中,
利用 (2.40) 对 (2.41) 进行代换, 我们得到
物体中任何一点的速度都可以用这个等式计算出来. 因此, 我们可以得出以下结论
- 物体在三维空间中的运动可以用一个 6 维向量
来表示, 它是物体线速度 和角速度 的组合.
2.3.2 两个物体的线速度和角速度
接下来, 我们将考虑两个在三维空间中运动的物体. 假设我们已经得到了这两个物体的局部坐标, 如下所示
第二个物体相对于第一个物体的位置和姿态为
因此, 第二个物体在世界坐标中的位置和姿态为
第二个物体的线速度可以通过对 (2.48) 关于时间求导得到.
其中,
这里, 利用 (2.48) 并重新排列其元素, 我们得到
图 2.12 坐标变换和角速度矢量
让我们思考一下第 2.2.4 节中的 (2.22)
这个方程的左边可以改写为
比较方程 (a) 和方程 (b) 可以看出
第二个物体的角速度可根据 (2.49) 计算如下
其中
从图 2.12 可以看出,
将
总之, 我们首先将物体 1 和物体 2 的位置和姿态定义为
物体的线速度和角速度被简单地合并在一起, 称为 "速度".
这里的
因此, 除了 (2.54) 中第三个元素对旋转速度的影响之外, 物体在世界坐标中的速度只是一个总和.
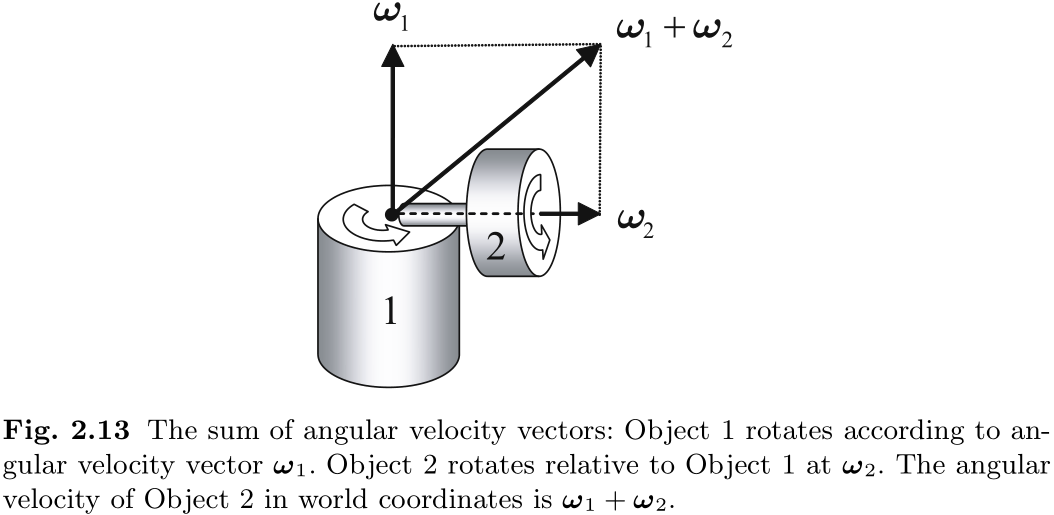
在图 2.13 中, 我们试图将 (2.55) 的含义形象化.
2.4 机器人数据结构和编程
2.4.1 数据结构
仿人机器人是由多个关节连接而成的机械装置. 在开始分析时, 我们希望将其划分为更小的单元. 在众多可能的分离方式中, 我们在图 2.14 中介绍了两种典型的方式.
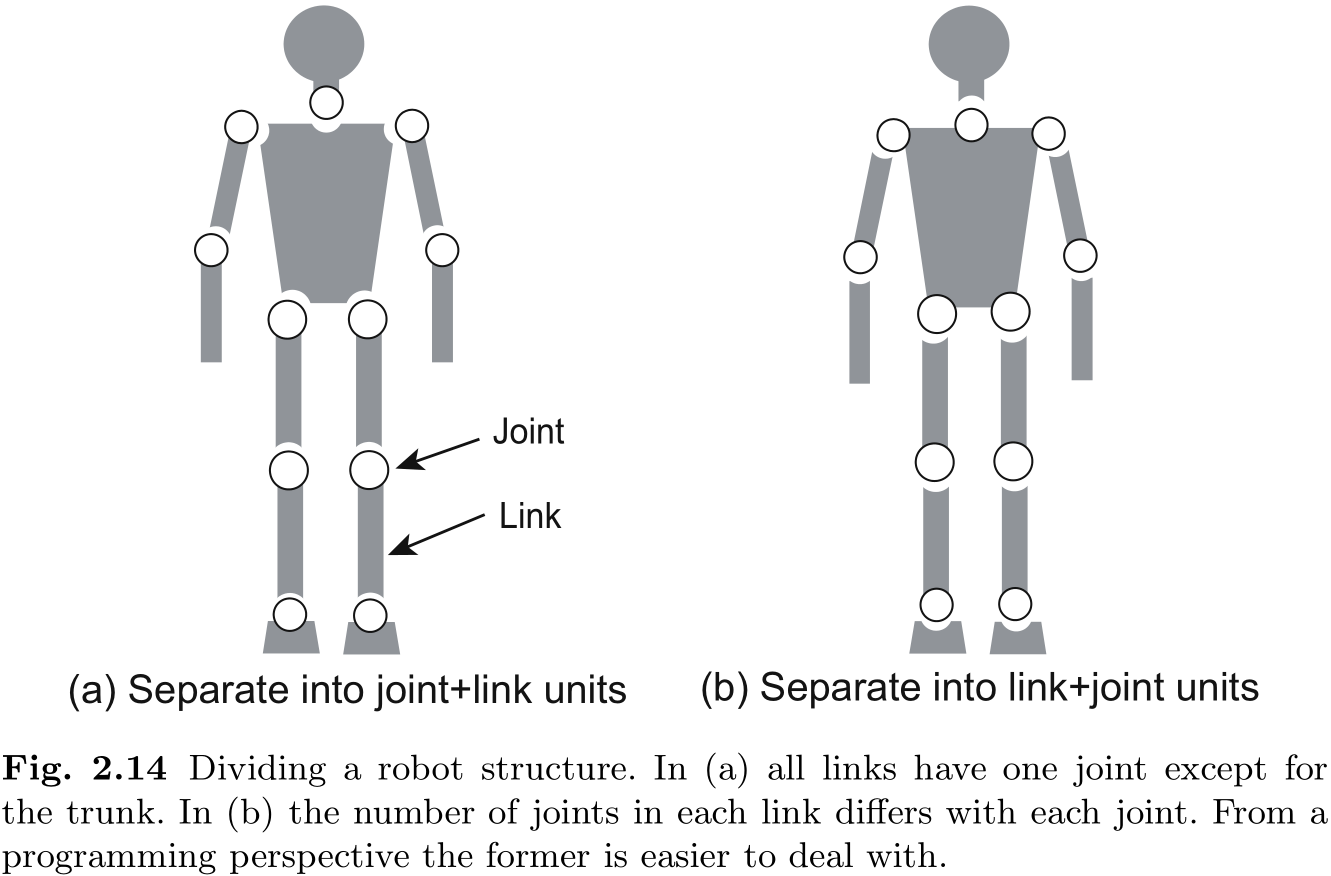
在图 2.14(a) 中, 每个关节都包含在离主干较远的链节中. 而在 (b) 中, 每个关节都被定义为主干或离主干较近的链节的一部分. 就计算机编程而言, 前一种方式更为方便. 原因是所有链节都只包含一个关节, 因此可以使用相同的算法来处理所有关节. 此外, 它还能让添加新关节变得更容易. 另一方面, 方法 (b) 将需要具有不同数量关节的链节. 这反过来又使计算机编程变得更加复杂. 请注意, 在这里我们讨论的是机器人的概念分隔. 并不是绝对要求将机器人分割得如图 2.14 所示.
将这些链节以正确的组合方式连接起来, 我们就得到了构成仿人机器人的链节组合. 连接规则由图 2.15 所示的树状图来表示.
树状图是一种结构图, 它有一个基部, 从基部分支出更小的分支, 但不会形成循环.
换句话说, 我们或许可以说, 这种结构显示了以基链节为共同祖先, 以末端链节为最年轻成员的链节家族树.
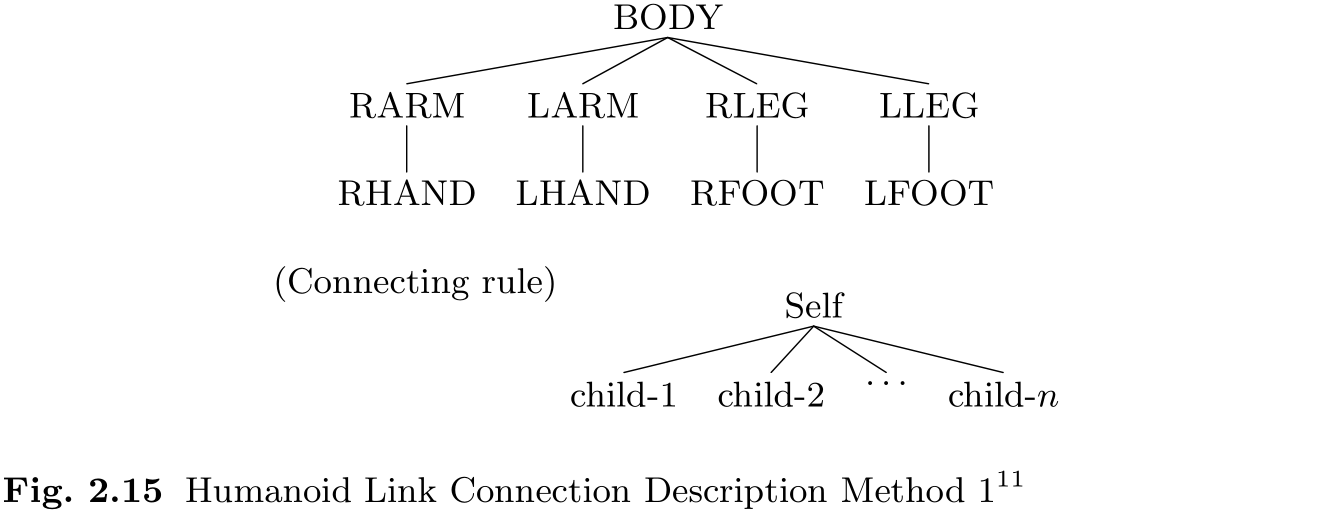
在给本教科书中的链节命名时, 我们使用 R 或 L 作为前缀来表示链节在哪一边. 因此, 右臂上的链节将使用 RARM, 左臂上的链节将使用 LARM.
然而, 在图 2.15 中, 根据链节的不同, 存在着不同数量的分支 (连接) , 因此正如我们在讨论机器人结构划分时所讨论的那样, 这种表示方法给编程带来了困难.
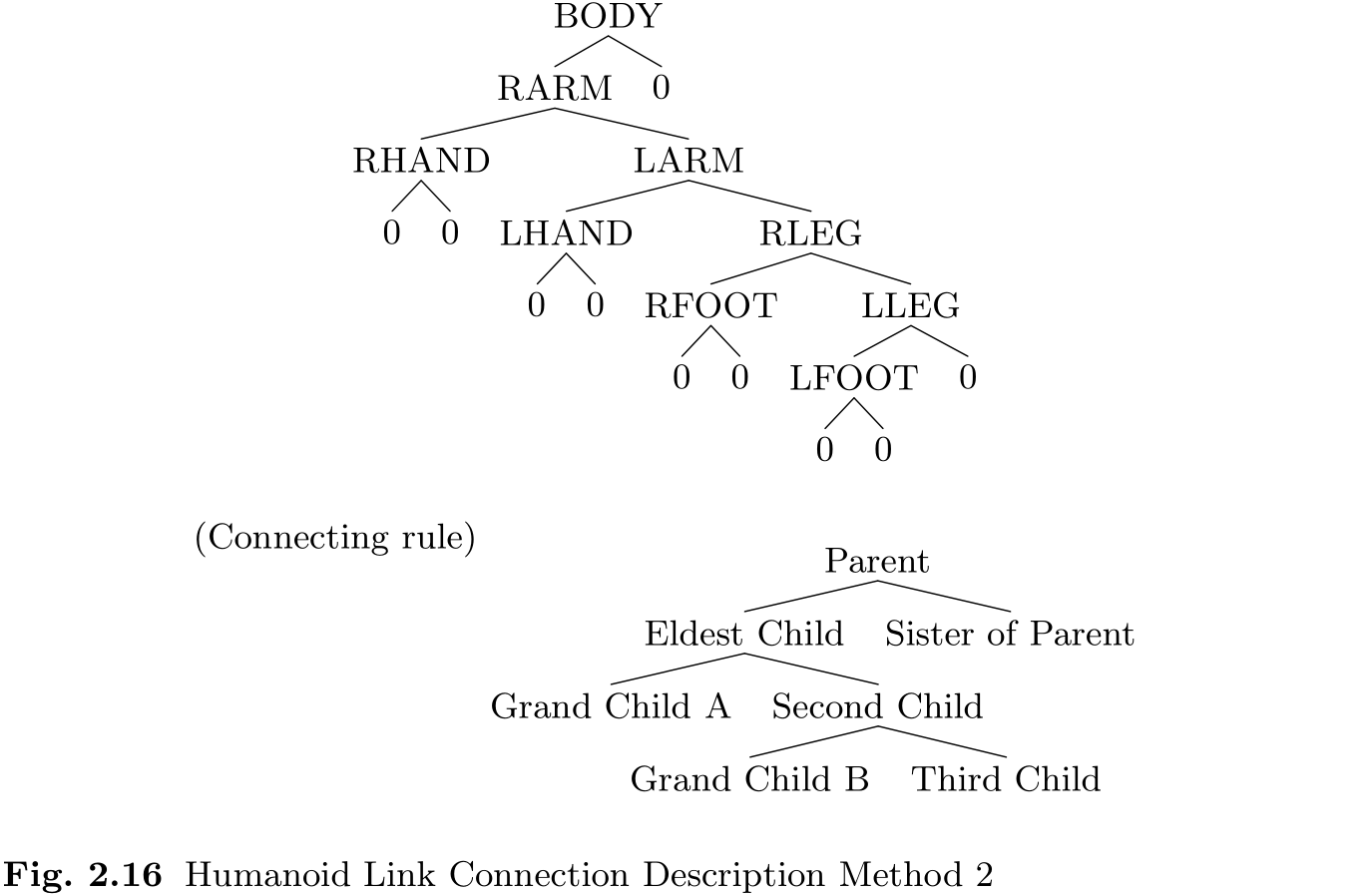
或者, 我们也可以如图 2.16 所示描述链节连接. 在该图中, 每个链节都有两条连接线, 左下线连接其子链节, 右下线连接其姊妹链节. 例如, 如果您想知道 RARM 的姊妹链节, 您可以沿着右下方的连接线找到 "LARM", "RLEG" 和 "LLEG" 链节. 这些链节的父链节是右上方的 "BODY" 链节, 子链节是左下方的 "RHAND" 链节. 在没有子链节或姊妹链节的末端, 我们使用了 "0". 总之, 虽然这个图表看起来不同, 但它所代表的信息与图 2.15 中的图表相同.
2.4.2 使用递归编程
接下来, 让我们看看如何实际实现一个使用这些数据结构的程序. 在准备过程中, 我们将把图 2.16 中的信息转换成列表. 2.16 中的信息转换成一个列表. 从 ID 编号 1 开始, 我们给每个链节一个 ID 编号, 并在下面的列表中使用.
| ID | name | sister | child |
|---|---|---|---|
| 1 | BODY | 0 | 2 |
| 2 | RARM | 4 | 3 |
| 3 | RHAND | 0 | 0 |
| 4 | LARM | 6 | 5 |
| 5 | LHAND | 0 | 0 |
| 6 | RLEG | 8 | 7 |
| 7 | RFOOT | 0 | 0 |
| 8 | LLEG | 0 | 9 |
| 9 | LFOOT | 0 | 0 |
要在 Matlab 中输入这些信息, 我们应键入以下内容.
在本教科书中, 我们将使用 Matlab, 它是 MathWorks 公司的产品, 可以让用户交互式地进行矩阵计算. 算法本身并不依赖于你所使用的语言, 因此这个程序也可以很容易地用其他语言 (如 C++ 或 Java) 来实现.
1 | >> global uLINK |
上面的 ">>" 是 Matlab 命令提示符. uLINK 是本教科书中使用的一个结构的名称, 它保存了计算中所需的大部分值. 这里我们只看 "name", "sister" 和 "child" 这几个字段. 在第一行中, 我们声明要使用全局变量 uLINK. 在接下来的行中, uLINK(1) 指向 ID 号为 1 的第一个 uLINK. 句号后的名称指定了数据字段名称 (name, sister, child) .
同样, 您也可以通过 uLINK(2) 访问 ID 号为 2 的链节部分中的字段.
一旦程序开始变长, 你就可以将这些命令存储到一个后缀名为 "m" 的文件中, 然后通过命令行执行.
1 | >> uLINK(1).name % print the name of the link with ID=1 |
如果在命令行中省略变量名后的分号 ";", Matlab 将打印出该变量的所有信息. 这样, 您就可以随时查看存储在该树中的信息. 换句话说, 您现在拥有了一个机器人链节信息数据库.
图 2.17 显示了一个简短的脚本 (PrintLinkName.m) , 它可以打印数据库中存储的所有链节名称.
图 2.17 PrintLinkName.m: 显示所有链节的名称
1
2
3
4
5
6
7function PrintLinkName(j)
global uLINK % Refer global variable uLINK
if j ~= 0
fprintf('j=%d : %s\n',j,uLINK(j).name); % Show my name
PrintLinkName(uLINK(j).child); % Show my child's name
PrintLinkName(uLINK(j).sister); % Show my sister's name
end
该程序将 ID 号作为输入, 并首先对其进行检查. 如果 ID 不为 0, 程序将打印相应的链节名称, 并使用姊妹 ID 编号调用 PrintLinkName, 然后使用子 ID 编号调用 PrintLinkName. 如果 ID 为 0, 程序将什么也不做. 将此脚本以 PrintLinkName.m 保存后, 我们就可以在 Matlab 命令行中执行 "PrintLinkName(1)", 并获得 "BODY" 链节下的树中子链节的名称. 从函数内部调用函数被称为递归调用. 每次调用该函数时, 都会在树中向下移动, 直到到达一个既没有姐妹节点也没有子节点的节点. 这为访问树中的每个节点并应用所需的计算提供了一种简单的方法.
利用递归调用技术, 我们可以轻松编写一个函数来求和所有链节的质量 (图 2.18) . 这里我们假设添加了一个新的数据字段 "m" 来保存链节的质量, 并用每个链节的实际质量对其进行初始化.
图 2.18 TotalMass.m: 每个链节的质量总和
1
2
3
4
5
6
7function m = TotalMass(j)
global uLINK
if j == 0
m = 0;
else
m = uLINK(j).m + TotalMass(uLINK(j).sister) + TotalMass(uLINK(j).child);
end
如果 ID 号为 0, 程序将返回 0 千克, 因为没有链节需要求和 (第 4 行) . 如果 ID 号不是 0, 那么程序将返回相应链节的质量, 姊妹链节的后代链节的总质量以及子链节的后代链节的总质量之和 (第 6 行) . 如果在命令行中输入 TotalMass(1), 该函数将访问树中的所有节点, 并返回 "BODY" 链节下所有链节的总质量. 与事先检查现有链节并求和的通常方法相比, 我觉得这个方法要聪明得多. 您觉得如何?
2.5 仿人机器人的运动学
2.5.1 创建模型
为了解释仿人机器人的运动学, 我们将使用图 2.19 所示的 12 DoF 模型, 该模型由两条腿组成. 链节名称及其 ID 编号如图 2.19(a) 所示. 按照图 2.14(a) 的方式分割该模型, 除了 "BODY" 链节外, 每个链节都只有一个关节驱动. 因此, 我们可以通过关节名称或其 ID 编号来识别链节. 例如 ID 编号 5 指的是 RLEG_J3 关节以及右小腿的链节.
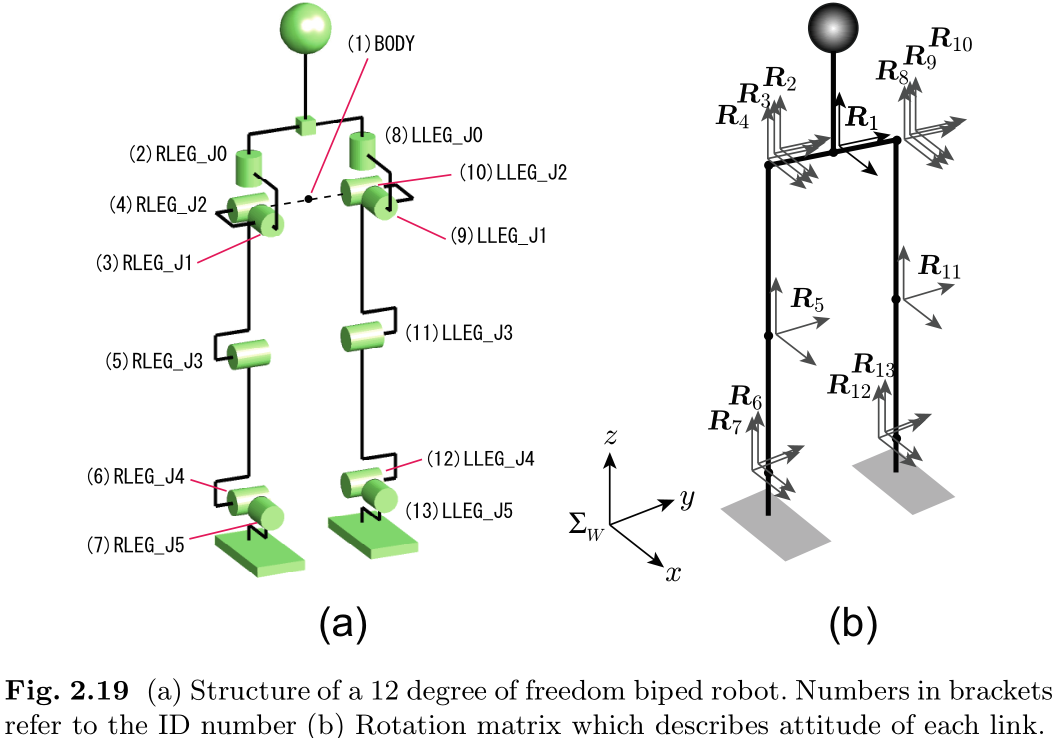
首先, 我们必须定义每个链节的局部坐标. 每个局部坐标的原点可以设置在其关节轴上的任何位置. 不过, 对于每个髋关节来说, 将三个坐标系的原点指定在三个关节轴相交的同一点是合理的. 同样, 对于每个踝关节, 我们将两个踝关节框架的原点指定在两个关节轴相交的同一点上.
然后, 将所有描述链节姿态的旋转矩阵设置为与机器人初始状态 (膝盖完全伸直直立) 时的世界坐标一致. 因此, 我们将 13 个矩阵设置为
图 2.19(b) 显示了在此阶段定义的局部坐标.
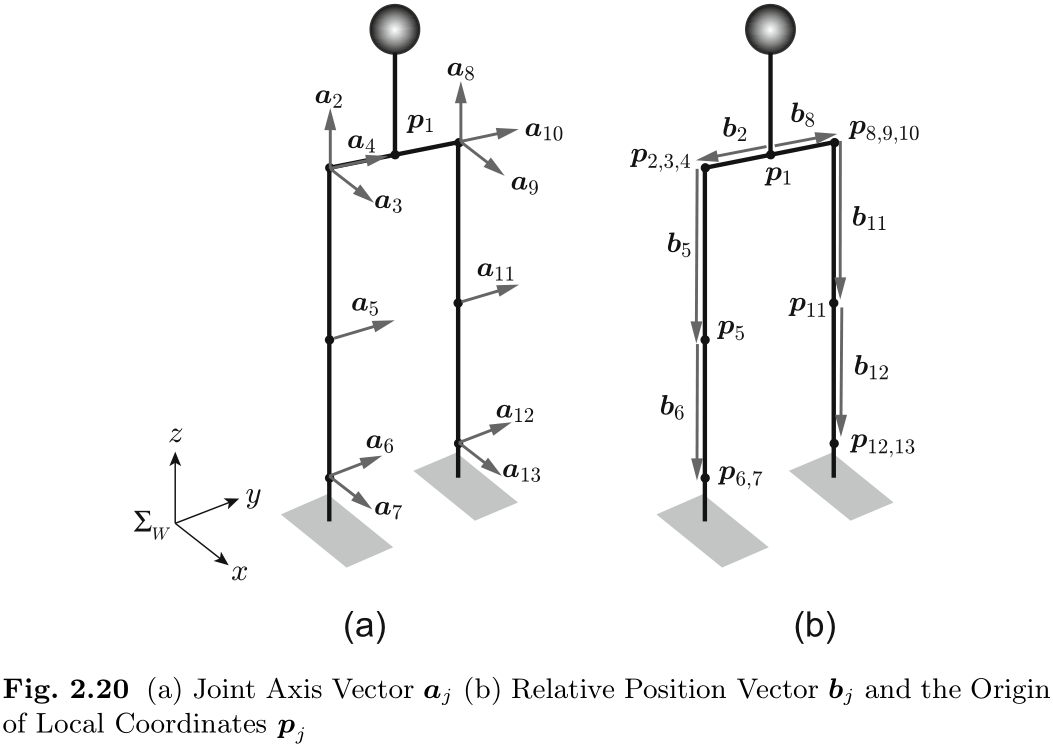
接下来我们将定义关节轴向量
有一种众所周知的方法可以用来描述机器人的链节结构, 叫做德纳维特-哈腾伯格 (Denavit-Hartenberg, DH) 法[18]. 我们最初也使用了这种方法. 不过, 这种方法有一个限制, 即需要改变每个链节坐标的朝向. 我们发现这种限制条件下的实现方法容易出错, 因此我们采用了上述方法.
在下面的章节中, 我们将利用上面的描述来计算正向运动学, 雅可比矩阵和逆向运动学. 为此, 我们需要更多的信息, 如形状, 关节角度, 关节速度等. 链节参数的完整列表如表 2.1 所示.
- 表 2.1 链节参数
| Link Parameter | Symbol for Equation | uLINK data field |
|---|---|---|
| Self ID | - | |
| Sister ID | None | sister |
| Child ID | None | child |
| Parent ID | mother | |
| Position in World Coordinates | p | |
| Attitude in World Coordinates | R | |
| Linear Velocity in World Coordinates | v | |
| Angular Velocity in World Coordinates | w | |
| Joint Angle | q | |
| Joint Velocity | dq | |
| Joint Acceleration | ddq | |
| Joint Axis Vector(Relative to Parent) | a | |
| Joint Relative Position(Relative to Parent) | b | |
| Shape(Vertex Information, Link Local) | vertex | |
| Shape(Vertice Information (Point Connections) | None | face |
| Mass | m | |
| Center of Mass(Link Local) | c | |
| Moment of Inertia(Link Local) | I |
2.5.2 正向运动学: 根据链节角度计算链节位置
正向运动学 (Forward Kinematics) 是一种通过给定的机器人结构及其关节角度来获取某一链节的位置和姿态的计算方法. 当您想计算整个机器人的质心时, 当您只想显示机器人的当前状态时, 或者当您想检测机器人与环境的碰撞时, 都需要用到正向运动学. 因此, 正向运动学构成了机器人仿真的基础.
正向运动学可以通过使用齐次变换的链式法则来计算. 首先我们先计算单链节的齐次变换, 如图 2.21 所示. 我们需要设置一个局部坐标系
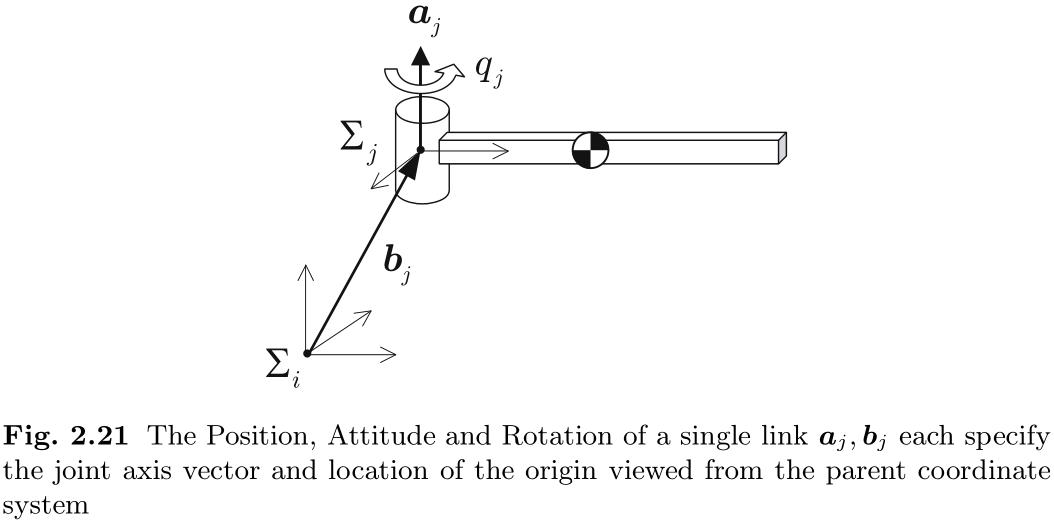
相对于父链节的齐次变换为:
接下来让我们假设有两条链节, 如图 2.22 所示. 我们假设父链节
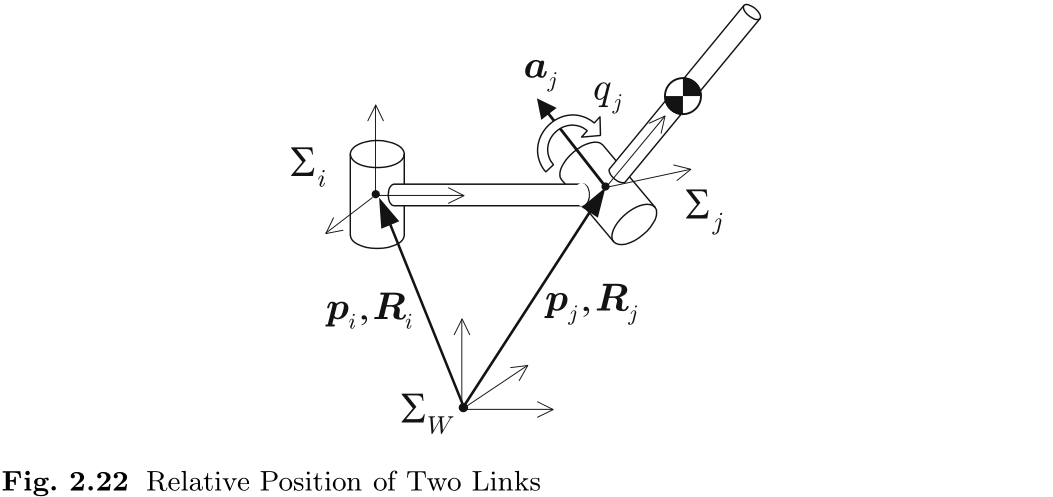
由齐次变换的链式法则可得
根据 (2.56), (2.57) 和 (2.58) 可以计算出
利用这种关系和递归算法, 正向运动学可以通过图 2.23 所示的一个极其简单的脚本来完成. 要使用这个程序, 我们首先要设置基础链节 (BODY) 的绝对位置和姿态以及所有关节角度. 然后通过执行 ForwardKinematics(1), 我们可以更新机器人所有链节的位置和姿态.
图 2.23 ForwardKinematics.m 计算所有关节的正向运动学参数
1
2
3
4
5
6
7
8
9
10function ForwardKinematics(j)
global uLINK
if j == 0 return; end
if j ~= 1
i = uLINK(j).mother;
uLINK(j).p = uLINK(i).R * uLINK(j).b + uLINK(i).p;
uLINK(j).R = uLINK(i).R * Rodrigues(uLINK(j).a, uLINK(j).q);
end
ForwardKinematics(uLINK(j).sister);
ForwardKinematics(uLINK(j).child);
图 2.24 显示了 12 自由度双足机器人在给定所有 12 个关节角度的随机值后的样子. 这应该有助于您想象一个简单的机构是如何体现大量复杂性的.
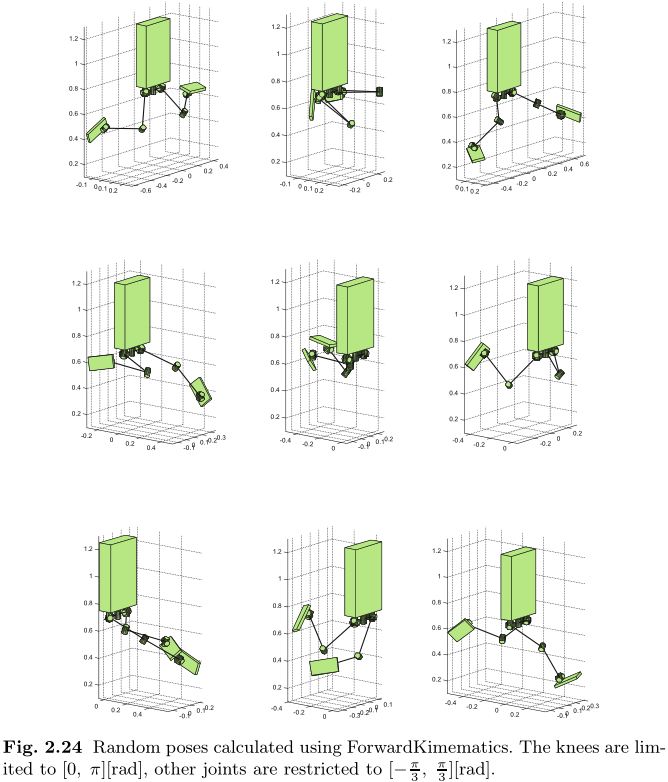
2.5.3 反向运动学: 根据链节的位置和姿态计算关节角度
接下来, 我们将讨论如何在获得身体和脚的位置和姿态的情况下计算关节角度. 在这种情况下, 我们需要做的是反向运动学 (Inverse Kinematics) . 例如, 假设我们的机器人位于楼梯前方, 我们希望将其中一只脚放在第一级台阶上, 而台阶的高度和深度是已知的. 我们当然需要确定髋关节, 膝关节和踝关节的旋转量. 在这种情况下, 反向运动学是必要的.
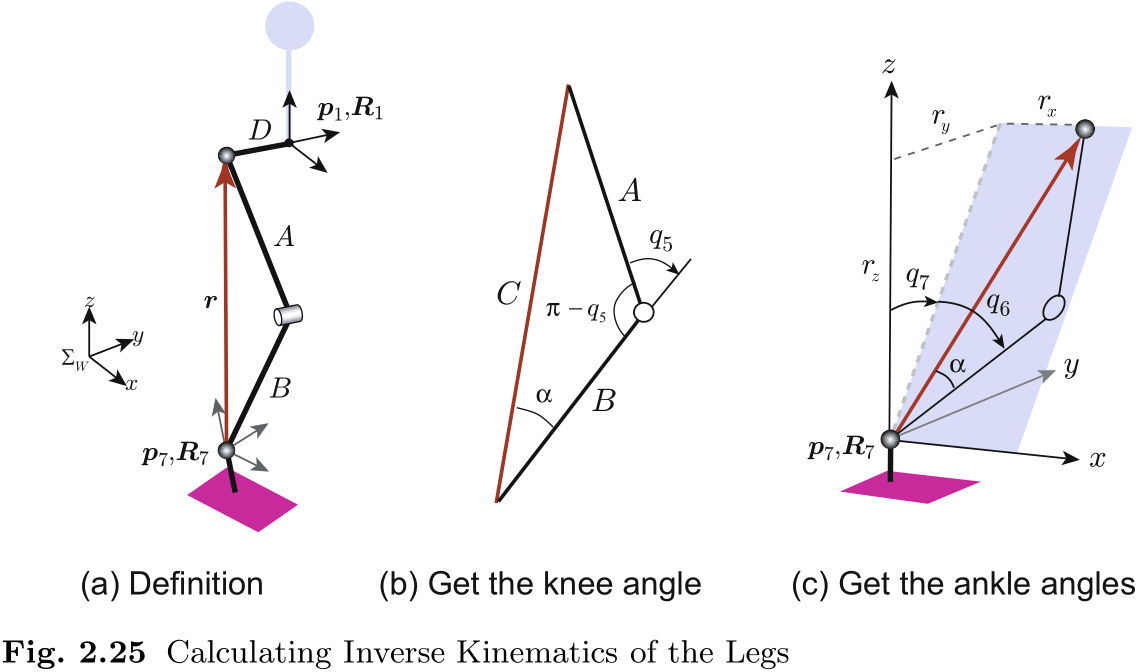
求解反向运动学有分析方法和数值方法. 首先, 我们将解释如何分析求解. 让我们把注意力集中在图 2.19 所示模型的右腿上. 身体和右腿的位置和姿态分别为 (
接下来, 我们计算从脚踝坐标空间看胯部的位置
由此我们可以计算出脚踝和髋关节之间的距离, 我们将其定义为
如图 2.25(b) 所示, 如果我们考虑三角形
因此, 膝盖的角度将是
如果我们将三角形下端的角度定义为
因此
接下来我们将重点讨论脚踝局部坐标. 如图 2.25(c) 所示, 从向量
函数
剩下的就是腿底部的偏航角, 滚动角和俯仰角. 根据定义每个关节的方程
可得
将方程左边的内容展开, 计算右边的内容, 可以得到以下结果
其中
仔细观察这个等式的左侧, 我们可以得到
图 2.26 展示了上述程序的实现过程. 对于左腿, 我们可以反转
在实际应用中, 我们的程序会覆盖超过腿长和关节角度限制的目标位置.
图 2.26 IK_leg.m 反向运动学分析解法的实施示例. 注意!在实际机器人上使用该程序时, 需要不断检查关节角度是否超出极限. 在最坏的情况下, 您可能会毁坏机器人或造成重大人员伤亡.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21function q = IK_leg(Body,D,A,B,Foot)
r = Foot.R' * (Body.p + Body.R * [0 D 0]'- Foot.p); % crotch from ankle
C = norm(r);
c5 = (C^2-A^2-B^2)/(2.0*A*B);
if c5 >= 1
q5 = 0.0;
elseif c5 <= -1
q5 = pi;
else
q5 = acos(c5); % knee pitch
end
q6a = asin((A/C)*sin(pi-q5)); % ankle pitch sub
q7 = atan2(r(2),r(3)); % ankle roll -pi/2 < q(6) < pi/2
if q7 > pi/2, q7 = q7-pi; elseif q7 < -pi/2, q7 = q7+pi; end
q6 = -atan2(r(1),sign(r(3))*sqrt(r(2)^2+r(3)^2)) -q6a; % ankle pitch
R = Body.R' * Foot.R * Rroll(-q7) * Rpitch(-q6-q5); % hipZ*hipX*hipY
q2 = atan2(-R(1,2),R(2,2)); % hip yaw
cz = cos(q2); sz = sin(q2);
q3 = atan2(R(3,2),-R(1,2)*sz + R(2,2)*cz); % hip roll
q4 = atan2(-R(3,1), R(3,3)); % hip pitch
q = [q2 q3 q4 q5 q6 q7]';
这种方法只能用于与图 2.19 中布局相同的机器人. 如果机器人的三个关节轴不相交于一点, 我们就需要一种完全不同的算法. 机器人教科书 (例如 [96, 127]) 中介绍了许多不同的算法, 但一般来说, 这些算法需要大量繁重的计算, 因此更常见的是使用数值解法, 我们将在下一节中详细介绍.
2.5.4 反向运动学的数值解法
与分析求解反向运动学相比, 正向运动学计算简单 (第 2.5.2 节) . 因此, 如图 2.27 所示, 使用正向运动学的试错法求解反向运动学并不遥远. 示例算法如下
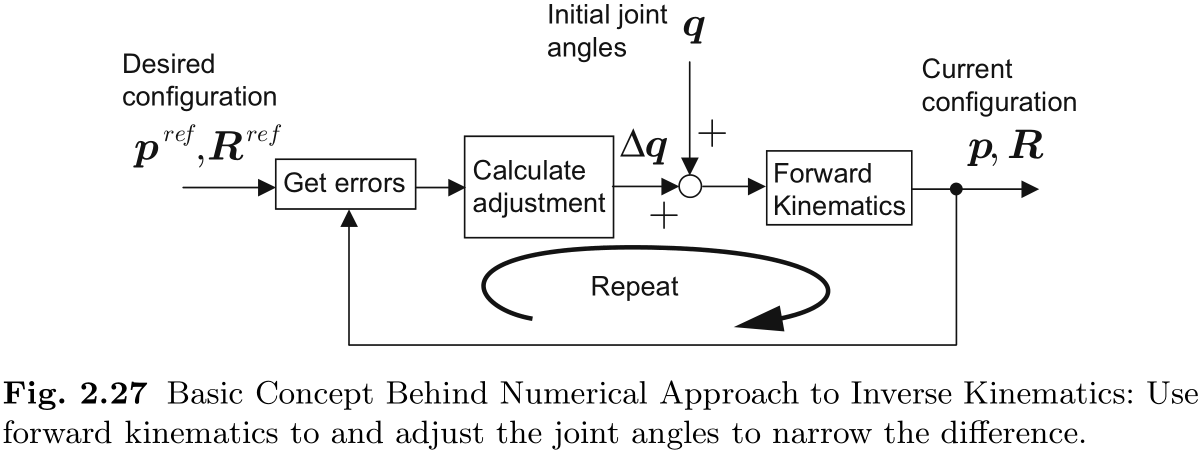
- 步骤 1. 准备基链节的位置和姿态
; - 步骤 2. 准备目标链节的位置和姿态
; - 步骤 3. 定义向量
, 其中包含从基链节到目标链节的关节角度; - 步骤 4. 使用正向运动学计算目标链节的位置和姿态
; - 步骤 5. 计算位置和姿态差
; - 步骤 6. 如果
足够小, 则停止计算; - 步骤 7. 如果
不够小, 则计算可减少误差的 ; - 步骤 8. 通过
更新关节角度, 返回步骤 4.
要真正实现这一点, 首先需要克服接下来的两个障碍.
- 我们所说的位置和姿态误差
足够小到底是什么意思? (步骤 6) - 我们究竟该如何计算
, 以减小误差? (步骤 7)
第一个问题相对容易解决. 零位置误差和零姿态误差可用以下公式描述
下面是一个根据误差大小返回正标量的函数示例
更一般的函数是
. 这里的 和 是某个正数, 需要更高精度的方向越大.
只有当位置和姿态误差都为零时, 该函数才会变为零. 当
那么第二个问题呢? 我们真正需要做的是找出一组关节角度
这个想法是任何人都会想到的, 但出于某种原因, 很多人往往认为只有他们才会想到. 事实上, 作者恰好就是其中之一 :-).
虽然这是一个诱人的想法, 但如今没有一个机器人会使用这种方法. 因为有一种方法更快, 更精确. 在这种被称为牛顿-拉夫逊法 (Newton-Raphson method) 的方法中, 我们首先要考虑的是, 在使用微小的
在这里,
这里的
矩阵
源自德国数学家 Carl Gustav Jacobi (1804-1851). 数学家提到 Jacobian 时, 指的是这个矩阵的行列式, 但机器人专家谈到 Jacobian 时, 通常指的是矩阵本身. 有些人认为这是一个错误, 但这并不是日本的专利, 全世界都在这样做.
有了 (2.70), 我们只需取该矩阵的逆, 就能计算出所需的调整量
这是根据位置和姿态误差计算关节角度调整的方程. 值
图 2.28 InvserseKinematics.m 反向运动学数值解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16function InverseKinematics(to, Target)
global uLINK
lambda = 0.5;
ForwardKinematics(1);
idx = FindRoute(to);
for n = 1:10
J= CalcJacobian(idx);
err = CalcVWerr(Target, uLINK(to));
if norm(err) < 1E-6 return, end;
dq = lambda * (J \ err);
for nn=1:length(idx)
j = idx(nn);
uLINK(j).q = uLINK(j).q + dq(nn);
end
ForwardKinematics(1);
end
函数 FindRoute 返回从基础链节到达目标链节所需经过的链节. CalcVWerr 是一个计算位置和姿态差的函数. 您可以在本章末尾的附录中找到这些函数的实现版本.
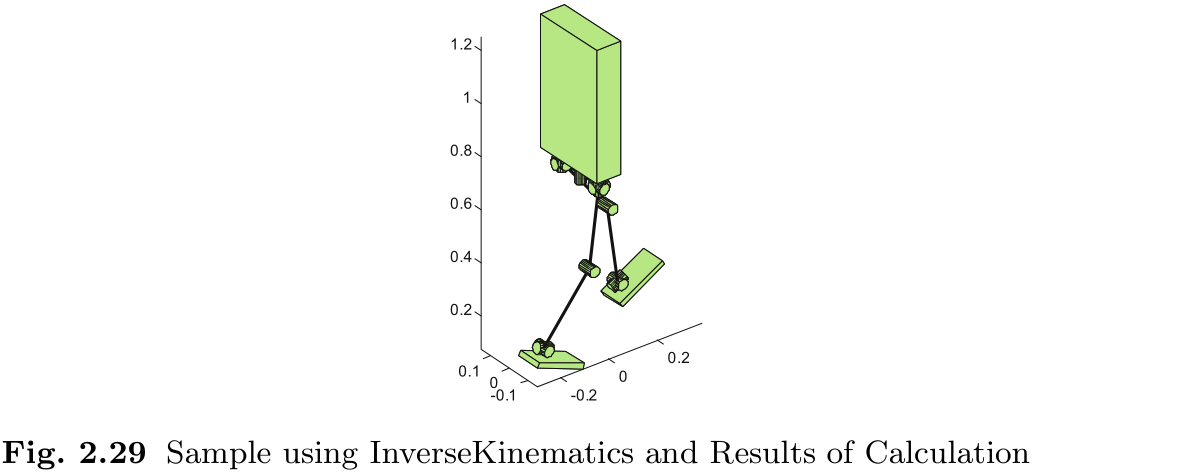
图 2.29 展示了将反向运动学作为 Matlab 命令输入的示例. 在这里, 我们使用 SetupBipedRobot 设置机器人数据, 使用 GoHalfSitting 获得非奇异姿态, 使用 DrawAllJoints() 显示双足机器人. 函数 rpy2rot() 是 (2.13) 的实现. 您可以从下载材料中获取这些信息.
图 2.29 使用逆运动学的样本和计算结果
1
2
3
4
5
6
7
8
9
10
11
12>> SetupBipedRobot; % Set robot parameters
>> GoHalfSitting; % Set knee bending posture
>> Rfoot.p = [-0.3, -0.1, 0]';
>> Rfoot.R = rpy2rot(0, ToRad*20.0,0);
>> InverseKinematics(RLEG_J5, Rfoot);
>> Lfoot.p = [ 0.3, 0.1, 0]';
>> Lfoot.R = rpy2rot(0, -ToRad*30.0,0);
>> InverseKinematics(LLEG_J5, Lfoot);
>> DrawAllJoints(1); % Show the robot![]()
2.5.5 雅可比 (Jacobian)
上一节我们介绍了雅可比矩阵, 它为您提供了小关节运动和空间运动之间的关系. 通过雅可比矩阵, 我们还可以计算出关节所需的力矩, 以便通过手脚产生外力. 由于雅可比矩阵被广泛应用于机器人控制领域, 因此没有雅可比矩阵的机器人学论文实在是凤毛麟角.
我们可以通过阅读 Yoshikawa 博士的教科书 [144], 了解雅可比矩阵在机器人学中的应用.
下面我们将介绍计算雅可比矩阵的实际过程. 图 2.30 显示了一条在空间中漂浮着
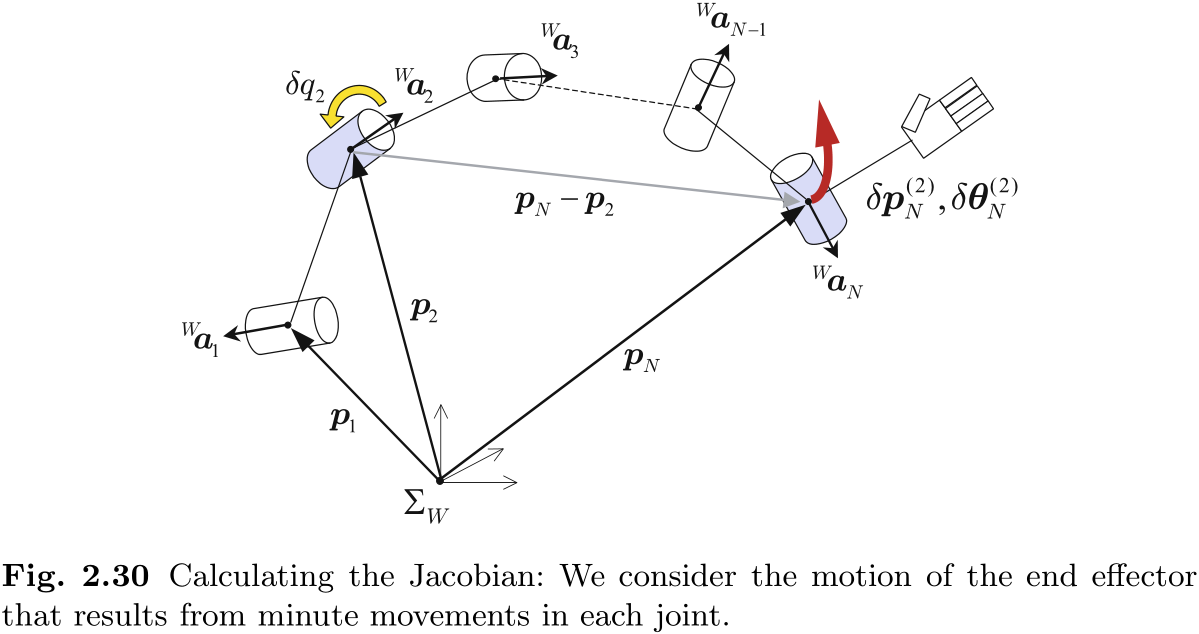
在这个链节中, 假设除了第 2 个关节外, 所有关节都保持固定, 我们将其转动一个小角度
其中,
如果我们对从第 1 节到第
我们可以将上式改写成矩阵, 得到
换句话说, 雅可比矩阵
以 Matlab 程序实现的这一过程如图 2.31 所示.
图 2.31 CalcJacobian.m: 计算雅可比矩阵
1
2
3
4
5
6
7
8
9
10
11function J = CalcJacobian(idx)
global uLINK
jsize = length(idx);
target = uLINK(idx(end)).p; % absolute target position
J = zeros(6,jsize);
for n = 1:jsize
j = idx(n);
mom = uLINK(j).mother;
a = uLINK(mom).R * uLINK(j).a; % joint axis in world frame
J(:,n) = [cross(a, target - uLINK(j).p) ; a ];
end
2.5.6 雅可比与关节速度
将 (2.70) 除以一小段时间
因此, 关节速度
请注意, 这是身体链节在空间中固定时的情况. 如果身体链节有自己的速度为
但在下面的讨论中, 为了简单起见, 我们假设主体链节在空间中是固定的. 我们可以通过 (2.75) 的变换计算出实现末端速度
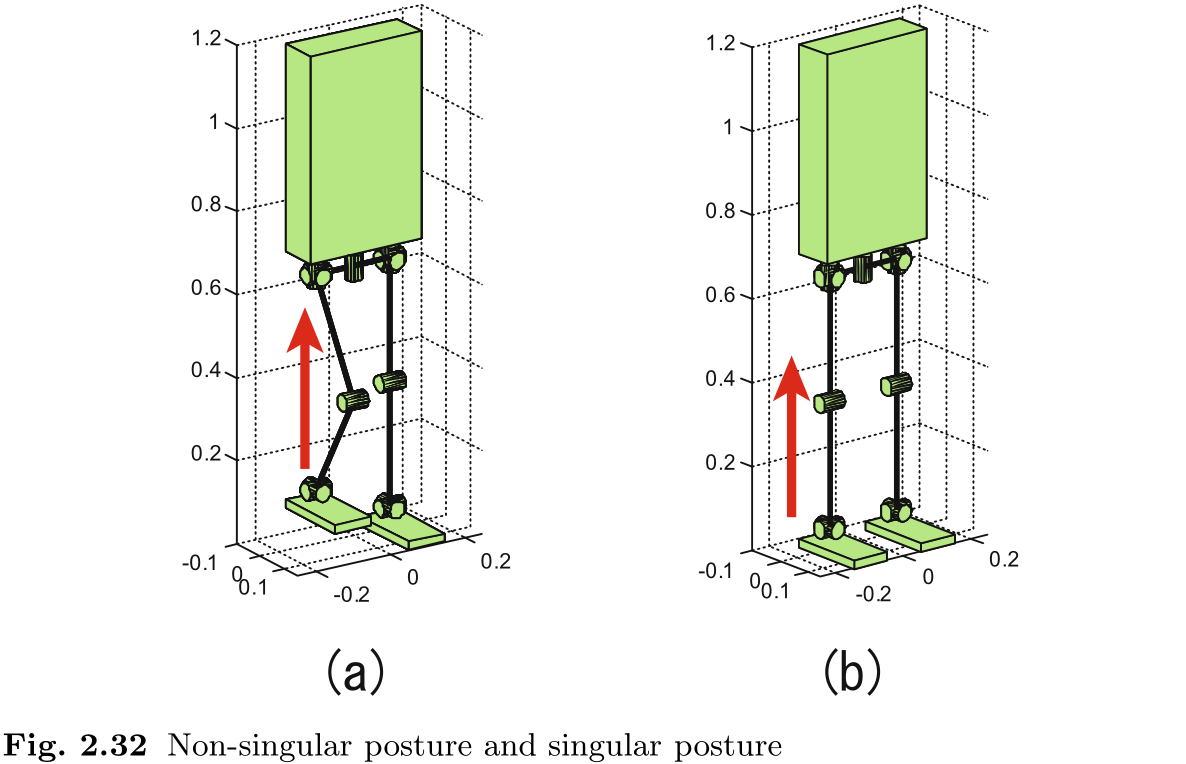
让我们来计算图 2.32(a) 中两种姿势的关节速度. 首先, 我们在 Matlab 命令行中设置机器人的所有几何信息, 然后使用 FindRoute() 查找从身体到右脚的路径. 然后使用 SetJointAngles() 设置关节角度, 使右侧髋关节俯仰角, 膝关节俯仰角和角俯仰角为 (-30, 60, -30) 度, 其他关节为 0 度. 我们可以通过以下输入计算雅可比矩阵.
1 | >> SetupBipedRobot; |
假设我们要让脚以 0.1m/s 的速度竖直抬起, 则关节速度可由 (2.77) 求得.
1 | >> dq = J \ [0 0 0.1 0 0 0]' |
从这一结果中我们可以看出, 髋关节俯仰, 膝关节俯仰和踝关节俯仰的关节速度分别为 (-0.3333, 0.6667, -0.3333) rad/s.
让我们尝试对图 2.32(b) 进行同样的计算, 图 2.32(b) 中的膝关节完全拉伸. 为此, 我们将右腿的所有关节角都置零, 计算雅可比矩阵, 并得出关节速度.
1 | >> SetJointAngles(idx,[0 0 0 0 0 0]) |
在这种情况下, 我们得到的警告信息是 "矩阵工作精度是奇异的", 并得到了一个由 NaN (非数字) 和 Inf (无穷大) 组成的关节速度向量. 因此, 计算在图 2.32(b) 的奇异姿势处崩溃, 此时膝关节完全拉伸.
机器人关节可能会因 NaN 和 Inf 等非法指令而失控. 因此, 我们必须提出警告和错误, 同时也要注意避免使用此类非法命令执行控制指令.
出现这种情况的原因是, 在这种配置下, 机器人无法通过施加任何关节速度来垂直移动其脚. 这种情况下的机器人姿态称为奇异姿态. 让我们观察一下在这种奇异姿态下雅可比矩阵的逆计算结果.
1 | >> J^(-1) |
2.5.7 奇异姿态
奇异姿势的例子如图 2.33 所示. 它们分别是: (a) 上一小节已经解释过的膝盖完全伸展的姿势;(b) 髋关节偏航轴和踝关节滚动轴对齐的姿势;以及 (c) 髋关节滚动轴和踝关节滚动轴对齐的姿势.
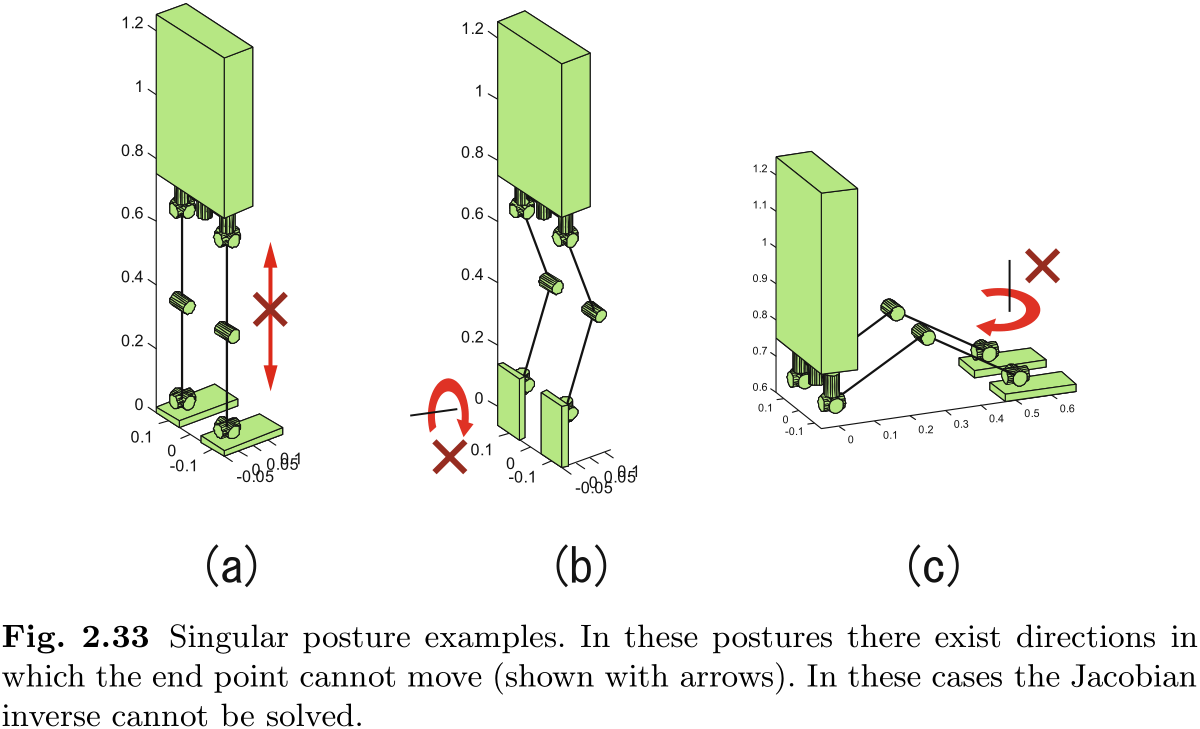
当机器人处于奇异姿态时, 雅可比矩阵会变成奇异矩阵, 我们无法计算其逆矩阵. 让我们检查一下图 2.33(b) 的情况.
1 | >> SetupBipedRobot; |
在进行逆计算时, 我们得到了一条警告信息和一个毫无意义的结果, 由于数值误差, 其分量大得不切实际 (
2.5.8 具有奇异鲁棒性的反向运动学
由于数值不稳定性, 第 2.5.4 节中的 Newton-Raphson 方法在奇异姿态附近无法正常工作. 让我们来观察一下.
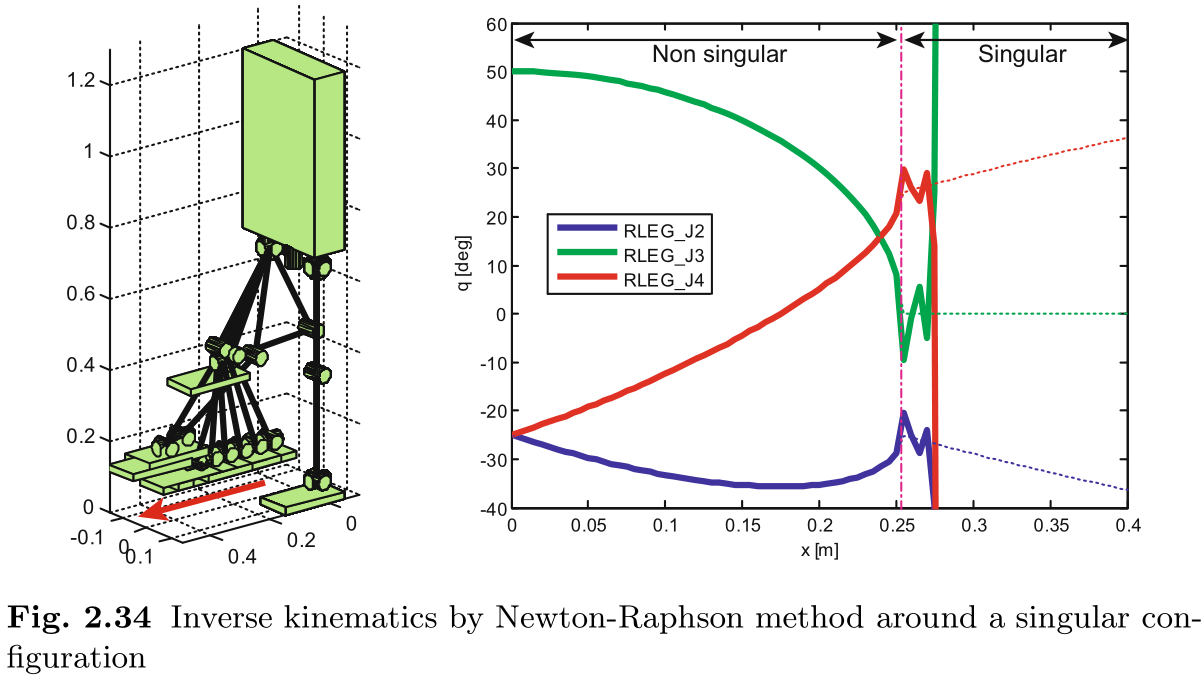
在图 2.34 中, 使用 Newton-Raphson 方法计算了让右脚从非弧形姿势向前移动时的关节角度. 右图显示了给定目标脚位置时的髋关节俯仰角, 膝关节俯仰角和踝关节俯仰角. 为便于比较, 用虚线表示了分析解. 脚的位置在垂直链线处达到奇点, 然后数值结果开始振动并偏离图表 (例如, 膝关节角度达到 8000 度以上) .
现在, 让我们再次考虑关节速度和末端执行器速度之间的关系, 其计算公式为
这里,
我们总能使误差
如果
将 (2.78) 和 (2.79) 代入, 可得
因此, 使
遗憾的是, 我们无法在奇异点处使用它, 因为
这意味着 (2.82) 右侧的逆式无法求解.
现在, 我们对成本函数稍作修改.
这将评估关节速度大小以及末端执行器速度误差. 关节速度通过增加正标量
其中,
即使在
矩阵
SR 代表 Singularity-Robust [138]. 它也被称为阻尼最小二乘逆 (Damped Least-Square (DLS) Inverse) [135].
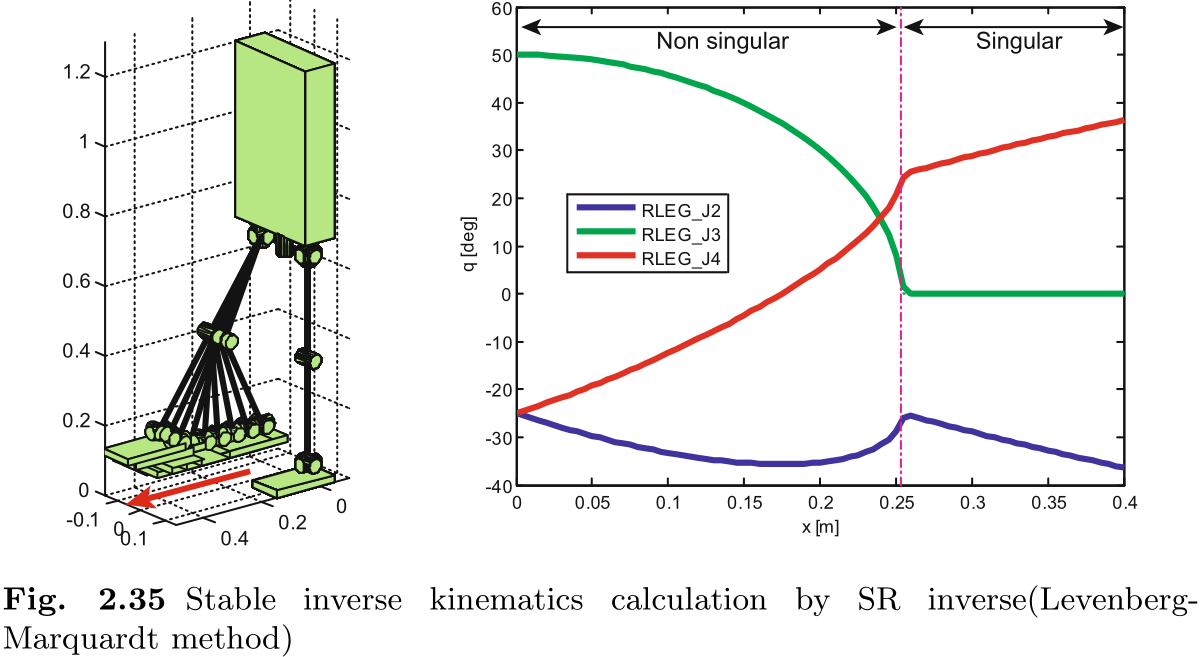
通过使用 SR 逆矩阵, 我们可以保证在奇点处稳定计算逆运动学. 图 2.35 显示了覆盖奇点的鲁棒稳定的反运动学计算, 图 2.36 显示了其算法. 为了实现快速, 稳健的计算, 应根据收敛程度修改参数
图 2.36 InvserseKinematics LM.m 用于处理奇异点的逆运动学算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27function err_norm = InverseKinematics_LM(to, Target)
global uLINK
idx = FindRoute(to);
wn_pos = 1/0.3;wn_ang = 1/(2*pi);
We = diag([wn_pos wn_pos wn_pos wn_ang wn_ang wn_ang]);
Wn = eye(length(idx));
ForwardKinematics(1);
err = CalcVWerr(Target, uLINK(to));
Ek = err'*We*err;
for n = 1:10
J = CalcJacobian(idx);
lambda = Ek + 0.002;
Jh = J'*We*J + Wn*lambda; % Hk + wn
gerr = J'*We*err; % gk
dq = Jh \ gerr; % new
MoveJoints(idx, dq);
err = CalcVWerr(Target, uLINK(to));
Ek2 = err'*We*err;
if Ek2 < 1E-12
break;
elseif Ek2 < Ek
Ek = Ek2;
else
MoveJoints(idx, -dq); % revert
break,
end
end
类似的优化问题经常出现在计算机视觉和机器学习中. 使用 SR 逆矩阵的迭代算法一般被认为是 Levenberg-Marquardt 方法的一个版本 [135].
2.5.9 附录: 补充函数
第 2.5.4 节及其后各小节中需要使用下面的函数来计算反运动学和雅可比矩阵的数值解.
图 2.37 FindRoute.m 查找从身体到目标链节的路径
1
2
3
4
5
6
7
8function idx = FindRoute(to)
global uLINK
i = uLINK(to).mother;
if i == 1
idx = [to];
else
idx = [FindRoute(i) to];
end图 2.38 SetJointAngles.m 沿指定索引设置关节角度
1
2
3
4
5
6
7function SetJointAngles(idx, q)
global uLINK
for n = 1:length(idx)
j = idx(n);
uLINK(j).q = q(n);
end
ForwardKinematics(1);图 2.39 CalcVWerr.m 计算位置和姿态误差的函数
1
2
3
4
5function err = CalcVWerr(Cref, Cnow)
perr = Cref.p - Cnow.p;
Rerr = Cnow.R^-1 * Cref.R;
werr = Cnow.R * rot2omega(Rerr);
err = [perr; werr];图 2.40 rot2omega.m 将旋转矩阵转换为相应的角速度向量 (2.39)
1
2
3
4
5
6
7
8
9
10function w = rot2omega(R)
el = [R(3,2)-R(2,3); R(1,3)-R(3,1); R(2,1)-R(1,2)];
norm_el = norm(el);
if norm_el > eps
w = atan2(norm_el, trace(R)-1)/norm_el * el;
elseif R(1,1)>0 && R(2,2)>0 && R(3,3)>0
w = [0 0 0]';
else
w = pi/2*[R(1,1)+1; R(2,2)+1; R(3,3)+1];
end